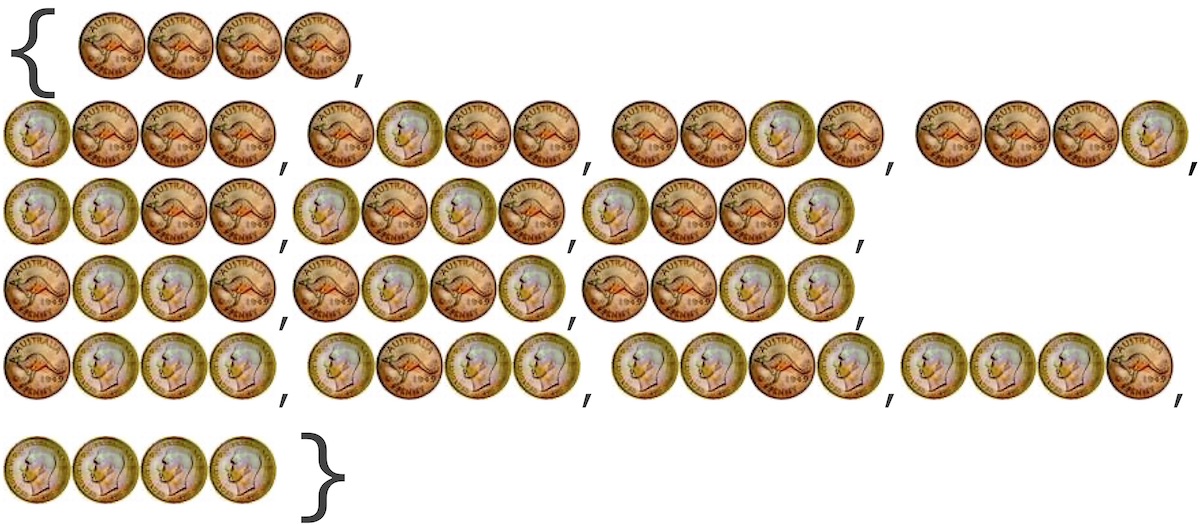
| HPS 0628 | Paradox | |
Back to doc list
For submission
1. Comment: "I have a way to play the lottery that gives an advantage. I run my own lottery privately using the same range of possible numbers. If my lottery draw is some number, say 1,234, I will then not choose that number on the real lottery. This works because the probability of both lotteries coming up with the same number is very small. There is a much greater chance that the two lotteries have different numbers. This is a terrific way to gain an advantage!"
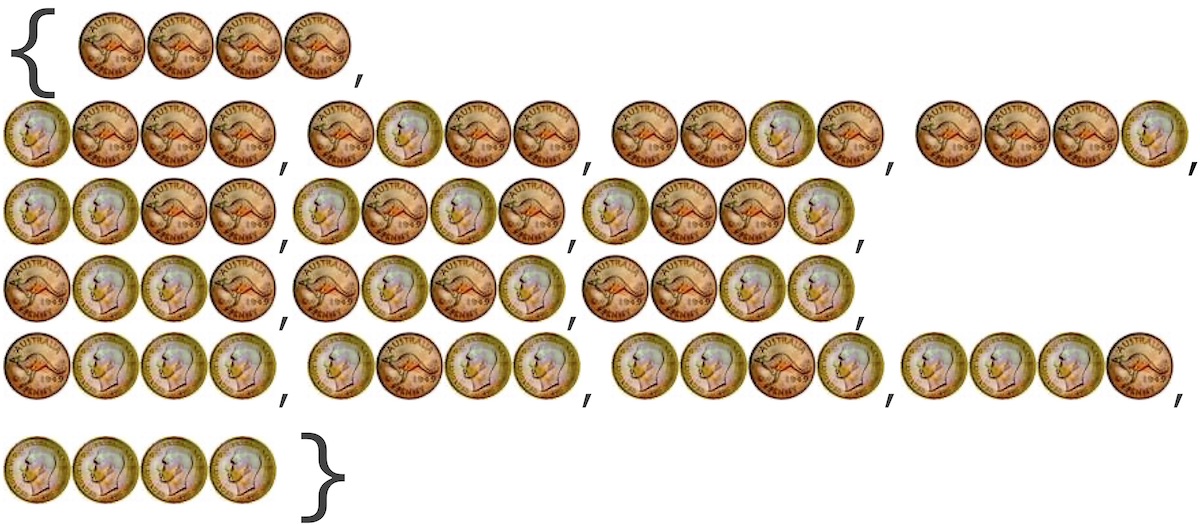
2a. For what is the above an outcome space?
2b. What must we assume about individual tosses if all the outcomes are to have equal probability?
For 2c, d and e, assume all the outcomes have equal probability.
2c. What is the expectation for the number of heads?
2d. What is the most likely number of heads?
2e. Consider the relative numbers of heads and tails. Which is more likely: that we have the same number of each? Or that we have three times as many of one as of the other?
Not for submission
A. How is it possible that we humans have survived so long in a chance filled world, given our evident difficulty with assessing chances correctly?
B. In the illustration of Simpson's paradox, there were two sorts of probabilities employed: P( cure | strong & severe ) and P( severe | strong ). How should we interpret each? The first pertains to the efficacy of a treatment and the second to the distribution of treatment over patients. Are they sufficiently similar in meaning so that we can combine them in one calculation?
C. The psychoanalyst, Carl Jung, explained his notion of "synchronicity" with many examples of the following type:
...
“coincidences” which were connected so meaningfully that their “chance”
concurrence would represent a degree of improbability that would have to
be expressed by an astronomical figure. By way of example, I shall mention
an incident from my own observation. A young woman I was treating had, at
a critical moment, a dream in which she was given a golden scarab. While
she was telling me this dream I sat with my back to the closed window.
Suddenly I heard a noise behind me, like a gentle tapping. I turned round
and saw a flying insect knocking against the window-pane from outside. I
opened the window and caught the creature in the air as it flew in. It was
the nearest analogy to a golden scarab that one finds in our latitudes, a
scarabaeid beetle, the common rose-chafer (Cetonia aurata),
which contrary to its usual habits had evidently felt an urge to get into
a dark room at this particular moment.
From Carl Jung "Synchronicity: An Acausal
Connecting Principle."
What are we to make of Jung's notion?
D. The Probability
Refresher asked the question "What
is probability?"
What is probability?