Research Statement

Gary D. Hart

Since childhood, I always wanted to be a scientist. Indeed, the search and need for knowledge and truth is a thirst that can never be quenched. Furthermore, there are so many areas that require Mathematics as the necessary tool for advancement and, not unlike the thrill the early explorers must have felt when faced with the frontiers during exploration, I wish to advance the cause and lives of mankind by doing cutting edge research.

My specific areas of interest is Optimization and Numerical Analysis. My most recent research projects and my thesis have involved using Optimization for the simulation of nonsmooth rigid multibody dynamics with contact and friction. Nonsmooth rigid multibody dynamics predicts the position and velocity evolution of a group of rigid particles subject to certain constraints and forces. Unfortunately, the classical acceleration-force approach does not necessarily have a solution with the Coulomb model for friction. This obviously poses several obstacles in the path of efficient simulation. This presents a perfect opportunity to blend Optimization and Numerical Analysis with my general areas of interest, namely, Functional Analysis, Linear Algebra, and Differential Equations.

Just as significant is the fact that out of scientific research spring exciting by-products, some of which are completely unexpected but useful. The discovery of these by-products is like finding gold. History is full of such examples. It is just possible that my research on my Ph.D. dissertation can produce some nuggets. This is just another reason why I am committed to the pursuit of scientific research.

Motivation of my recent area of research

Simulating the dynamics of a system with several rigid bodies and with joint, contact, noninterpenetration, and friction constraints is an important part of many research areas, e.g. virtual reality, robotics simulations, rock dynamics, and structural engineering. It is thus expected that progress in simulating such phenomena will have a positive impact upon many such important areas.

A virtual reality driving simulator is currently being developed with the hope of helping patients, for example soldiers or car accident victims, recover from post-traumatic stress disorder. Moreover, virtual reality exposure (VRE) therapy is used to cure fears of heights, flying, public speaking, and thunderstorms. [19, 25, 24]

The U.S. military has extreme interest in robotic simulation for use on the battlefield. One particular need is the use of self-driving vehicles. The medical operating rooms have been invaded by robots, that work with surgeons to save lives. In the first half of 2003, the demand for robots increased by 26 per cent, which at that time was the highest growth ever recorded.

Scientific context and previous approaches

Friction makes the simulation particularly difficult because there may be no acceleration solution (Painleve Paradox) even when the velocity solution exists, so extra care must be taken. If the system has only joint constraints, then the problem is a differential algebraic equation (DAE) [11, 18]. However, the non-smooth nature of the noninterpenetration and friction constraints requires the use of specialized techniques.

Approaches used in the past for simulating rigid multi-body dynamics with contact and friction include piecewise DAE approaches [18], acceleration-force linear complementarity problem (LCP) approaches [12, 15, 29], penalty (or regularization) approaches [14, 26], and velocity-impulse LCP-based time-stepping methods [6, 8, 27, 28]. When the value of the time step is set to 0, the LCP of the velocity-impulse approach is the same as the one used in the compression phase of multiple collision resolution [16].

Of all these approaches, the penalty approach is probably the most encountered mechanical engineering literature. It accommodates the non-smooth nature of contact and friction by smoothing their mathematical descriptions. The advantage of this approach is that it is easy to set up and results in a DAE, for which both analytical and software tools are in a fairly mature state of development. The disadvantages are that finding a priori appropriate values for the smoothing parameters is difficult and that it results a very stiff problem even for moderate time steps.

The LCP method represents both contact and friction as inequality constraints that are computationally treated as hard constraints. The advantage of this method is that there are no extra parameters to tune and no artificial stiffness. It may therefore be expected to work better with less user input. On the other hand, the subproblems are now constrained by inequalities, and separate analysis and software tools need to be developed to make the approach successful.

The velocity impulse LCP based approach that we use has the advantage that it does not suffer from the lack of a solution that can appear in the piecewise DAE and acceleration-force LCP approach [12, 27]. It also does not suffer from the artificial stiffness that is introduced by the penalty approach.

My accomplishments in the smooth shape approach

I have developed a method [3] that achieves geometrical (noninterpenetration and joint) constraint stabilization for complementarity based time-stepping methods for rigid multi-body dynamics with contact, joints, and friction. Such a method avoids the constraint drift that appears even in the DAE case following the index reduction procedure. A variant of the scheme developed by me and co-authors is currently used for the dynamical simulation of dynamical robotic grasps [5, 23]. This scheme needs no computational effort other than that for solving the basic LCP subproblem, though the free term of the LCP is modified compared with other time-stepping LCP approaches [6, 7, 28].

The constraint stabilization issue in a complementarity setting has been tackled by using nonlinear complementarity problems [28], an LCP followed by a nonlinear projection approach that includes nonlinear inequality constraints [7], and a post-processing method [13] that uses one potentially non-convex LCP based on the stiff method developed in [7] followed by one convex LCP for constraint stabilization. When applied to joint-only systems, the method from [13] belongs to the set of post-processing methods defined in [9, 10]. In order to achieve constraint stabilization, however, all of these methods need additional computation after the basic LCP subproblem has been solved. This stands in contrast with this approach that needs no additional computational effort to achieve constraint stabilization.

The LCP method represents both contact and friction as inequality constraints that are computationally treated as hard constraints. The advantage of this method is that there are no extra parameters to tune and no artificial stiffness. It may therefore be expected to work better with less user input. On the other hand, the subproblems are now constrained by inequalities, and separate analysis and software tools need to be developed to make the approach successful. [17]

Assume, for now, that the mappings defining the joint and noninterpenetration constraints are differentiable. If the shapes are such the mappings are differentiable only for small values of the interpenetration, then the analysis of this work can be extended, in a straightforward though laborious manner, as in [3] to demonstrate the constraint stabilization effect.

1. We defined a method that achieves constraint stabilization while solving only linear complementarity problem per step [3]. Our method does not need to stop and detect collisions explicitly and can advance with a constant time step and predictable amount of effort per step. We proved that the velocity stays bounded and that the constraint infeasibility is uniformly bounded in terms of the size of the time step and the current value of the velocity.

2. In [5] we extended our method to a version with an adjustable parameter γ , and the constraint stabilization effect was shown to hold for any γ ∈ (0, 1] An application of this method was used in a robotic grasp simulator [23].

In Figure 1, we see two frames of a robot simulation consisting of a glass that is within the reach of a Bartlett hand that starts to close.

Figure 1: Two frames of a robot simulation

3. We have shown that the solution set of the LCP subproblem may be nonconvex for arbitrarily small friction [2]. However, even in this case, we can find two iterative methods that converge linearly with a fixed convergence rate to a solution point, at least for small values of the friction coefficient [4], while solving only convex subproblems that can be solved in polynomial time.

The result is especially intriguing since problems with nonconvex solution sets rarely have polynomial time solutions. Figure 2 shows a two-dimensional cannonball arrangement simulation involving 21 bodies

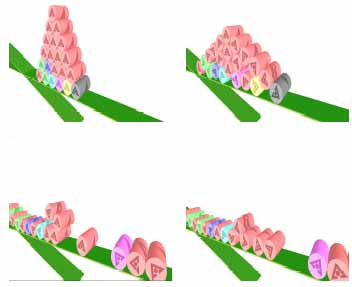
Figure 2: Two-dimensional cannonball arrangement

4. We have shown that our method can be applied to interesting phenomena, such as size-based segregation, with 4 order of magnitude larger time steps while essentially capturing the same dynamics [17].

Example: Brazil Nut Effect Simulation. See Figure 3

� Time step of 100ms, for 50s. 270 bodies.

� Convex Relaxation Method. One QP/step. No collision backtrack.

� Friction is 0.5, restitution coefficient is 0.5.

� Large ball emerges after about 40 shakes. Results in the same order of magnitude as MD simulations (but with 4 orders of magnitude larger time step).

Figure 3: Brazil Nut Example

Nonsmooth shaped bodies research

In all cases, the need for computing a distance between objects becomes vital. In physical simulations, for example, collisions and interpenetration among objects must be detected. The minimum Euclidean distance is usually used to compute the distance between separated objects. But when penetration exists, we cannot use this minimal Euclidean distance to describe the extent of the penetration.

Allowing a controllable amount of penetration between bodies is useful, since it allows one to take larger time steps, and it results in much faster methods. In particular, many of the schemes developed by us work with constant time steps. Hence will we need to develop a useful measure of distance if we want to determine the depth of penetration in the case of nonsmooth shaped bodies.

Since any body can be approximated by a finite union of convex, smooth-shaped bodies, we could extend, in principle, the analysis for approximation of any configuration. Probably, however, it is computationally more efficient to accommodate non-smooth or non-convex shapes directly, by working with a piecewise smooth mappings for the distance constraints. With the intention of extending results with smooth bodies to non- smooth or non-convex bodies, it is my intention to advance research in this specific area. I have already started preliminary investigation.

A natural next step might be to move towards the analysis of contact with non-smooth bodies. This makes it imperative that we improve upon our current method of detection of collisions or penetrations. Suppose that we could produce a metric that was equivalent to the Minkowski-type ones proposed in [1, 20, 21], but with the advantage that penetration is simple to determine computationally, see Figure 4. I have analyzed such a metric and one of the truly remarkable aspects of the use of this metric is its simplicity, in that it only involves solving a linear programming problem. Thus it can handle convex polyhedral bodies and provide us with an elegant, yet simple way to detect collision and penetration of two bodies.

Figure 4: Demonstration of Penetration Depth

I have shown that this new metric is equivalent, in the usual sense, to the current metrics being studied for penetration depth. Moreover, one great advantage is that computing this indicator function has complexity O(m + n), where m, n are the facets of the polyhedra, due to results on the complexity of linear programming in R3 [22]. This compares much favorably with previous results for Miinkowski metrics that have a worst case complexity at best O(m² + n² ) [20, 21].

Theoretically, this approach can be used for problems in any fixed dimension. We have succeeded in simulating a true three-dimensional problem, see Figure 5 Future research possibilities exist, as we will probably want to examine whether higher order methods are possible and feasible. In addition, we will have to examine and possibly refine our approach to energy restitution after a collision.

Figure 5: True Three-Dimensional Case

Future work and applications

Advances in these research areas may soon be used in such diverse areas as nuclear reactors. In particular, there seems to be an ongoing debate about the feasibility of nuclear energy using Pebble Bed Modular Reactors. Therefore, I am excited at the endless possibilities that research can allow and, even though the rewards are definitely priceless, I plan to request funding from NSF, DOE (pebble bed reactor applications), and Defense research programs (DOD, ARO, NRO, for the robotics applications), NIH (fluid flow with densely packed particles for drug design).

Clearly, there are many more challenges ahead. Our formulation does not, for example, include the case of elastic bodies. Also, does the geometric size of the problem escalate, for enormously large numbers of multi-faceted polyhedra? Of great importance is the question of whether the results are consistent in the limit as the polyhedro become spheres. Finally, I expect our results to be relevant to multibody dynamics inside multiphysics, such as particles in flow.

Since inquiring minds want to know, I am truly interested in satisfying my desire to inquire. That is a desire only research can fulfill. I am looking forward to the opportunity to make a positive contribution to the scientific world.

References

[1] P. K. Agarwal, L. J. Guibas, S. Har-Peled, A. Rabinovitch, and M. Sharir, Penetration depth of two convex polytopes in 3d, Nordic Journal in Computing, 7 (2000), pp. 227�240.

[2] M. Anitescu and G. D. Hart, Solving nonconvex problems of multibody dynamics with joints, contact, and small friction by successive convex relaxation, Mechanics Based Design of Structures and Machines, 31 (2003), pp. 335�356.

[3] ______ A constraint-stabilized time-stepping approach for rigid multibody dynamics with joints, contact and friction, International Journal for Numerical Methods in Engineering, 60 (2004), pp. 2335�2371.

[4] ______ A fixed-point iteration approach for multibody dynamics with contact and small friction, Mathematical Programming, 101 (2004), pp. 3�32.

[5] M. Anitescu, A. Miller, and G. D. Hart, Constraint stabilization for time-stepping approaches for rigid multibody dynamics with joints, contact and friction, in Proceedings of the 2003 ASME International Design Engineering Technical Conferences, Chicago, Illinois, 2003, American Society for Mechanical Engineering. ANL/MCS-P1023-0403.

[6] M. Anitescu and F. A. Potra, Formulating dynamic multi-rigid-body contact problems with friction as solvable linear complementarity problems, Nonlinear Dynamics, 14 (1997), pp. 231�247.

[7] ______ On integrating stiff rigid multibody dynamics with contact and friction, in Contact Mechanics. Proceedings of the 3rd Contact Mechanics International Symposium, Praia de Consola c ̃ao, Peniche, Portugal, June 17-21, 2001, Dordrecht, Netherlands, 2002, Kluwer Academic Publishers.

[8] M. Anitescu, F. A. Potra, and D. Stewart, Time-stepping for three-dimensional rigid-body dynamics, Computer Methods in Applied Mechanics and Engineering, 177 (1999), pp. 183�197.

[9] U. M. Ascher, H. Chin, L. R. Petzold, and S. Reich, Stabilization of constrained mechanical systems with daes and invariant manifolds, J. Mech. Struct. Mach, 23 (1995), pp. 135 � 158.

[10] U. M. Ascher, H. Chin, and S. Reich, Stabilization of daes and invariant manifolds, Numerische Mathematik, 67 (1994), pp. 131�149.

[11] U. M. Ascher and L. R. Petzold, Computer methods for ordinary differential equations and differential-algebraic equations, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1998.

[12] D. Baraff, Issues in computing contact forces for non-penetrating rigid bodies, Algorithmica, 10 (1993), pp. 292�352.

[13] M. B. Cline and D. K. Pai, Post-stabilization for rigid body simulation with contact and constraints, in Proceedings of the IEEE International Conference in Robotics and Automation, IEEE, 2003.

[14] B. R. Donald and D. K. Pai, On the motion of compliantly connected rigid bodies in contact: a system for analyzing designs for assembly, in Proceedings of the Conf. on Robotics and Automation, IEEE, 1990, pp. 1756�1762.

[15] C. Glocker and F. Pfeiffer, An lcp-approach for multibody systems with planar friction, in Proceedings of the CMIS 92 Contact Mechanics Int. Symposium, Lausanne, Switzerland, 1992, pp. 13�30.

[16] ______ Multiple impacts with friction in rigid multi-body systems, Nonlinear Dynamics, 7 (1995), pp. 471�497.

[17] G. D. Hart and M. Anitescu, A hard-constraint time-stepping approach for rigid multibody dynamics with joints, contact, and friction, in Proceedings of the Richard Tapia Celebration of Diversity in Computing Conference 2003, J. Meza and B. York, eds., New York, NY, USA, 2003, ACM Press, pp. 34�41.

[18] E. J. Haug, Computer Aided Kinematics and Dynamics of Mechanical Systems. Vol. 1: Basic Methods, Allyn & Bacon, Inc., Needham Heights, MA, USA, 1989.

[19] L. Hodges, P. L. Anderson, G. C. Burdea, H. G. Hoffman, and B. O. Rothbaum, Treating psychological and physical disorders with vr, IEEE Computer Graphics and Applications, (2001), pp. 25�33.

[20] Y. J. Kim, M. C. Lin, and D. Manocha, Deep: Dual-space expansion for estimating penetration depth between convex polytopes, in Proceedings of the 2002 International Conference on Robotics and Automation, vol. 1, Institute for Electrical and Electronics Engineering, 2002, pp. 921�926.

[21] Y. J. Kim, M. A. Otaduy, M. C. Lin, and D. Manocha, Fast penetration depth computation for physically-based animation, in Proceedings of the 2002 ACM Siggraph/Eurograph symposium on Computer Animation, J. Hodgins and M. van de Panne, eds., San Antonio, Texas, 2002, Association for Computing Machinery, pp. 21 � 33.

[22] N. Megiddo, Linear-time algorithms for linear programming in r3 and related problems, SIAM Journal on Computing, 12 (1983), pp. 759�776.

[23] A. Miller and H. I. Christensen, Implementation of multi-rigid-body dynamics within a robotic grasping simulator, in IEEE International Conference on Robotics and Automation, 2003, pp. 2262�2268.

[24] B. O. Rothbaum, L. Hodges, P. L. Anderson, L. Price, and S. Smith, Twelve-month follow-up of virtual reality and standard exposure therapies for the fear of flying, Journal of Consulting and Clinical Psychology, 70(2) (2002), pp. 428�432.

[25] B. O. Rothbaum, L. Hodges, D. Ready, K. Graap, and R. D. Alarcon, Virtual reality exposure therapy for Vietnam veterans with posttraumatic stress disorder, Journal of Clinical Psychiatry, 62(8) (2001), pp. 617�622.

[26] P. Song, P. Kraus, V. Kumar, and P. Dupont, Analysis of rigid-body dynamic models for simulation of systems with frictional contacts, Journal of Applied Mechanics, 68 (2001), pp. 118�128. [27] D. E. Stewart, Rigid-body dynamics with friction and impact, SIAM Review, 42 (2000), pp. 3�39.

[28] D. E. Stewart and J. C. Trinkle, An implicit time-stepping scheme for rigid-body dynamics with inelastic collisions and coulomb friction, International Journal for Numerical Methods in Engineering, 39 (1996), pp. 2673�2691.

[29] J. Trinkle, J.-S. Pang, S. Sudarsky, and G. Lo, On dynamic multi-rigid-body contact problems with coulomb friction, Zeithschrift fur Angewandte Mathematik und Mechanik, 77 (1997), pp. 267�279.