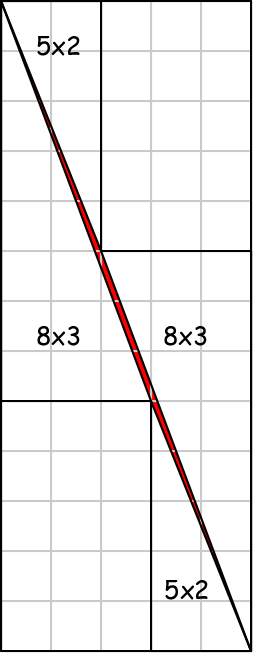
Where does the extra unit square of area come from when we move the rectangles and triangles from the 8x8 square to the 13x5 rectangle?
In short, the triangles that abut the diagonal of the enclosing 13x5 rectangle don't quite fit. They leave a tiny gap that is hard to see unless the figure is drawn very accurately. The gap has unit area.
In more detail:
The diagonal of the 13x5 rectangle has a gradient of 13/5 = 2.6.
The diagonal of the 8x3 triangle has a gradient of 8/3 = 2.666.
The diagonal of the 5x2 triangle has a gradient of 5/2 = 2.5.
The result is that the hypotenuses of the 8x3 and 5x2 triangles fall just short of the diagonal of the enclosing 13x5 rectangle. As a result they do not quite meet up with the hypotenuses of the 8x3 and 5x2 triangles on the other side of the hypotenuse. That shortfall creates the small gap (shown in red) in which the missing unit area is distributed.
