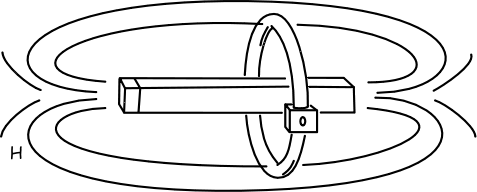
Magnet and conductor at rest in the ether
John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Pittsburgh PA 15260.
Homepage: www.pitt.edu/~jdnorton
This page is available at www.pitt.edu/~jdnorton/goodies
Einstein was driven to conceive and believe his special theory of relativity through seven and more years of grappling with problems in electrodynamics. It is not so easy to see how his ideas in electrodynamics demand the new kinematics of special relativity. Here the connection is illustrated in a simple example.
Einstein later recounted how quite early he became convinced that the induced electric field of his celebrated magnet and conductor thought experiment had a purely relative existence. Some observers find it; some do not. In a simple thought experiment, this relative existence can be seen to force the relativity of simultaneity, the essential departure of Einstein's new kinematics from Newtonian notions.
While Einstein surely eventually came to see the connection, we do not know if it played a role in his early explorations prior to 1905.
The text below is based on Sections 4.1-4.2 of John D. Norton, "Einstein’s Special Theory of Relativity and the Problems in the Electrodynamics of Moving Bodies that Led him to it." in Cambridge Companion to Einstein, M. Janssen and C. Lehner, eds., Cambridge University Press.
| The decisive moment in Einstein’s path to special relativity came when he reflected on the interaction of a magnet and conductor in Maxwell’s electrodynamics. The outcome was of such enduring importance that, years later when he wrote his 1905 paper on special relativity, this was the elementary consideration to which he gave pride of place in the paper’s first paragraph. As far as Maxwell’s theory is concerned, the case of a magnet at rest in the ether is very different from that of one that moves. As shown in Figure 8 the magnet at rest is surrounded just by a static magnetic field H | The version I will develop is a slight variant form given by August Föppl (Einführung in die Maxwell’sche Theorie der Elektricität. Leipzig: B. G. Tuebner, 1894.) in an electrodynamics text which Einstein probably read. |

Magnet and conductor at rest in the ether
The moving magnet, however, is
surrounded by both a magnetic field H
and an electric field E. The latter
arises from the complicated interactions between electric and magnetic fields
in Maxwell’s electrodynamics. At a point in space as the magnet moves
past, the magnetic field will wax and wane. A time varying magnetic field
induces an electric field, a new entity not present in the first case.
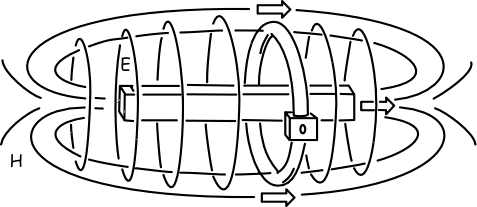
Magnet and conductor moving in the ether
Since the theory holds the two cases to be so distinct, one would expect that a simple measurement would distinguish them. The most straightforward would be to encircle the magnet with a conductor; that is, a wire with free charges in it that would be set in motion by the electric field to generate a measurable electric current. The conductor surrounding the magnet at rest would show no current; the conductor moving with the moving magnet would show a current and reveal its absolute motion. Or so one would expect. However another electrodynamical interaction intervenes.
Since the charges of the moving conductor are themselves moved through the magnetic field, that field also exerts a force on them and produces a current. The two currents—one due to the induced electric field, the other due to the motion of the charges in the magnetic field—are in opposite directions and turn out to cancel exactly. In both cases, there is no measurable current. Once again we have an experiment aimed at detecting motion in the ether, this time using a simple detector made from a magnet and a wire. And again we find a null result.
Einstein (1920, “Fundamental Ideas and Methods of the theory of Relativity, Presented in Their Development,” Papers, Vol. 7, Doc. 31.) later recalled how disturbed he was by the tension between the theoretical account and experimental outcome:
"The idea, however, that these were two, in principle different cases was unbearable for me. The difference between the two, I was convinced, could only be a difference in choice of viewpoint and not a real difference. Judged from the [moving] magnet, there was certainly no electric field present. Judged from the [ether], there certainly was one present. Thus the existence of the electric field was a relative one, according to the state of motion of the coordinate system used, and only the electric and magnetic field together could be ascribed a kind of objective reality, apart from the state of motion of the observer or the coordinate system. The phenomenon of magneto-electric induction compelled me to postulate the (special) principle of relativity."
The principle of relativity, which prevailed among the observables, had to be extended to the full theory. This thought experiment gave Einstein the means to do it. The existence of the induced electric field was no longer the immutable mark of a magnet truly in motion; it was now merely an artifact of motion relative to the observer. Whatever may be the magnet’s inertial motion, an observer moving with it will see a pure magnetic field; an observer in another state of inertial motion will see a mixture of magnetic and electric fields. That is just what moving magnetic fields look like, Einstein supposed—just as, in the later special theory of relativity, observers see moving clocks slow and rods shrink, while co-moving observers do not.
| With this notion of field transformations, Einstein had created a potent device and it remained of central importance. For it was how Einstein would finally show in 1905 that Maxwell’s electrodynamics conformed to the principle of relativity after all. The difficulty Einstein faced, however, was that no fully relativistic formulation of Maxwell’s electrodynamics was possible just using this new device of field transformations. It had to be coupled with the novel account of space and time in special relativity. A simple thought experiment—not due to Einstein—shows that the device of field transformations requires Einstein’s later notion of the relativity of simultaneity if it is to be implemented in a relativized Maxwell’s theory. | A simpler argument is that Maxwell’s theory entails the constancy of the speed of light and that constancy, along with the principle of relativity, entails the relativity of simultaneity. This simpler argument, however, does not reveal how the kinematics of special relativity must permeate through even the simplest electrodynamical processes if the principle of relativity is to be respected; showing that is the function of this magnet and coil thought experiment. |
Consider a very long coil of wire with a rectangular cross
section. When a current is passed through the coil, a uniform magnetic field H appears inside, with the magnetic
field running along the axis of the coil. The wire consists of a lattice of
immobile positive charges, with the current due to the motion of negatively
charged electrons. The density of positive and negative charges will balance
exactly so the wire carries no net charge. A section through the coil is
shown below, as it is seen by the “co-moving observer,” an
observer who moves with the coil.
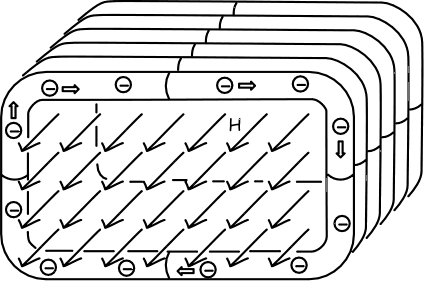
Magnetic field inside a coil as seen by a co-moving observer
We now set the coil into uniform motion. The next figure below shows how it will appear to a “resting observer,” that is, one who remains at rest while the magnet moves past. Following Einstein’s prescription, a resting observer will see an induced electric field E associated with the magnetic field. From the case of the magnet and conductor (above) we can see that the induced electric field will be perpendicular to both the magnetic field and the direction of motion. Since the magnetic field is uniform, the induced electric field will be uniform as well and it will run from the bottom of the coil to the top.
Since there is no magnetic field outside an infinitely long coil, the electric field lines of force will terminate in the wire. Maxwell’s theory is clear on what that means: electrical lines of force can only terminate in charges. The result is that the top of the coil carries a net negative charge and the bottom a net positive charge, both of which are not seen by the co-moving observer.
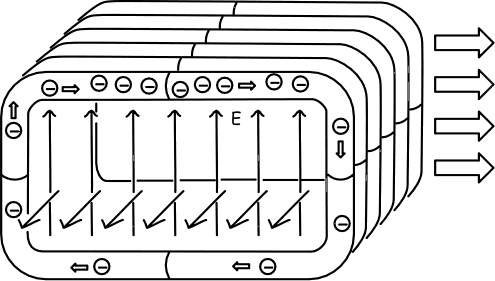
Induced electric field inside a moving coil
| How can this happen? The co-moving observer judges the current carrying electrons to take the take the same time to move from left to right as from right to left. The resting observer does not. They take more time to traverse the coil in the left to right direction (with the motion) and less in the other direction (against the motion). As a result, there is an accumulation of negative charges on the top and dilution of negative charges on the bottom of the coil, yielding net negative and positive charges respectively. | An analogy: on a circular track, racing cars will accumulate on the slow side and dilute on the fast side. |
This difference of traversal times cannot happen in classical (Galilean) kinematics. If one observer judges the two traversal times to be equal, then so must all observers.
| The difference can arise in special relativistic kinematics; it is a direct expression of the relativity of simultaneity. The effect is a familiar expression of it in the case of light signals. | If, for example, a light signal bounces between ends A and B of a rod, an observer at rest on the rod judges the traversal times to be equal. But that is not so for an observer who judges the rod to move in the direction of A to B. For that observer, the light signal traversing from A to B needs more time to catch the fleeing end B; and the light signal traversing from B to A requires less time to meet the approaching end A. This disagreement immediately leads to the two observer's differing judgments concerning the simultaneity of the events at A and B; that is, to the relativity of simultaneity. |
This thought experiment shows that sufficient pursuit of Einstein’s device of field transformations in Maxwell’s electrodynamics must eventually force the relativity of simultaneity. The device cannot be used satisfactorily for the realizing of the principle of relativity until Einstein adopts the novel account of space and time of special relativity.
The thought experiment is not Einstein’s. We do not know the precise path that Einstein took from these field transformations to the space and time transformations of special relativity. He may have used physical reasoning such as in the thought experiment. Or he may have arrived at the result by mathematical analysis of the formal properties of Maxwell’s equation, much as we might imagine Lorentz doing. Or he may have used both. We do know, however, that it took years and that several other considerations entered.
July 31, 2006