

home >> lectures>>Tuebingen Summer School


Idealizations are used routinely in the physical sciences. Commonly, their use is unproblematic. However there are many cases in which they introduce difficulties that may pass unnoticed and thereby compromise the analysis and our understanding of its foundations. These five lectures will investigate idealizations of this problematic type, mostly in statistical physics.
Monday, July 27, 2015; 20:00-22:00
Terms like "idealization," "approximation" and "model" appear throughout the philosophy of science literature, but without standard definitions. To enable clear analysis, I propose definite meanings for the first two.
An approximation is an inexact description of a target system. It is propositional.
An idealization is a real or fictitious system, distinct from the target system; and an exact description of some of its properties is also an inexact description of some aspects of the target system. Idealizations are distinguished from approximations in that only idealizations involve reference to a novel system.
This difference is important when idealizations are created by taking infinite limits, such as is done often in statistical mechanics. For these infinite limits may have strange properties, much odder than the discontinuities of phase transitions now widely acknowledged in the literature. The limits may yield no systems at all. Or they may yield limit systems whose properties differ in important ways from all those systems used to take the limit.
As a result, these infinite limits may fail to provide idealizations at all and we may have only approximations, that is, inexact descriptions. I will argue that various forms of the thermodynamic limit are an instance of this failure.
Are phase transitions a banner instance of emergence or treated reductively by renormalization group methods? The answer depends on how you define levels between which the relations of reduction and emergence obtain.
Reading
"Approximation and Idealization: Why the Difference Matters" Philosophy of Science, 79 (2012), pp. 207-232.
"Infinite Idealizations," European Philosophy of Science--Philosophy of Science in Europe and the Viennese Heritage: Vienna Circle Institute Yearbook, Vol. 17 (Springer: Dordrecht-Heidelberg-London-New York), pp. 197-210.
Confusions over Reduction and Emergence in the Physics of Phase Transitions, in my Goodies pages.
Tuesday, July 28th, 2015; 10:00-11:00
Thermodynamically reversible processes play a central role in thermodynamics. They are the least dissipative processes. The standard Clausius definition of thermodynamic entropy depends upon them. Yet their treatment in the thermodynamics literature is almost universally inadequate, even by authors who seek precision in the foundations of thermodynamics. They are routinely described as sequences of equilibrium states, which cannot evolve since they are at equilibrium; and also states minutely removed from equilibrium, so that they can evolve. The two properties are obviously incompatible, but nonetheless routinely combined with little proper apology.
A more cautious analysis identifies a lack of care in treating the limits used to define the processes. Using the framework of the first lecture, these processes turn out not to be idealizations but approximations. I also identify a troublesome privileging of equilibrium state spaces over non-equilibrium systems as one of the principal causes of the confusion in the literature.
Reading
John D. Norton, "The Impossible Process: Thermodynamic Reversibility." Draft.
Giovanni Valente, "On the Paradox of Reversible Processes in Thermodynamics."
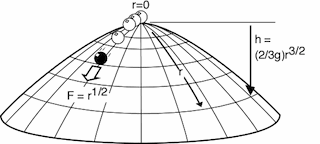
Wednesday, July 29th, 2015; 10:00-11:00
The "dome" is the simplest instance of many systems in Newtonian theory that exhibit indeterminism. It is a system that remains completely quiescent for an arbitrary time and then springs into motion. The debate over whether such systems are properly classified as Newtonian has proved revealing. It has forced us to reflect critically over which idealization are admissible in physical theories and even what Newtonian theory really is. Finally it has drawn attention to a notion of possibility central to the practice of physicists--"being physical"--that has otherwise eluded philosophical scrutiny.
Reading:
John D. Norton, "The Dome: An Unexpectedly Simple Failure of Determinism" Proceedings of the 2006 Biennial Meeting of the Philosophy of Science Association, Philosophy of Science, 75, No. 5, (2008). pp. 786-98. Download.
John D. Norton, "The Dome: A Simple Violation of Determinism in Newtonian Mechanics." Goodies page.
Samuel C. Fletcher, "What Counts as a Newtonian System? The View from Norton's Dome." http://philsci-archive.pitt.edu/8833/ (Preprint for European Journal for Philosophy of Science 2.3 (2012): 275–297.)
Thursday, July 30th, 2015; 10:00-11:00
Friday, July 31st, 2015; 10:00-11:00
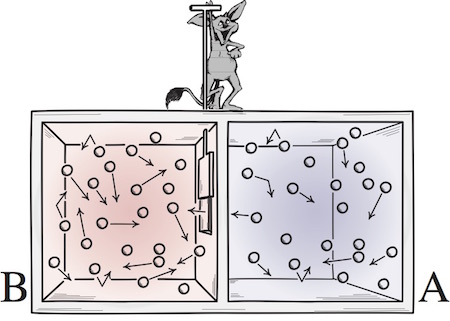
These last two lectures will examine two misplaced idealizations in the literature on Maxwell's demon.
A Maxwell demon is a molecular scale device that is able to manipulate individual molecules. In Maxwell's original design, the demon operated a door separating two gas chambers so that faster molecules collected in one chamber and the slower molecules in the the other. Can it, as Maxwell suggested a century and half ago, reverse the second law of thermodynamics?
A loose consensus has emerged that the demon must fail for a general and principled reason. The demon is idealized as an information processing device or computer and, it is urged, the hidden entropic cost of information processing eradicates any entropy reduction brought about by the demon's operation. The original exorcism of Szilard and Brillouin located the overlooked entropy cost as arising when the demon gains information about molecular positions. That early view has been replace by a later one based on Landauer's principle. It urges that the demon must remember these molecular positions and that the entropy cost arises only when the demon erases this memory.
This entire analysis, I will argue, is at best speculation still in need of proper support; or at worst an accumulation of mistakes in thermal physics.
The latter verdict involves two sorts of misplaced idealizations:
(Lecture 4) 1. A Maxwell demon operates by accumulating small, entropy reducing thermal fluctuations. Yet the arguments used to support Landauer's principle depend essentially on idealized processes that selectively neglect fluctuations.
These arguments depend in many places on the idea that a thermodynamically reversible process can be implemented to arbitrary accuracy on molecular scales. Under both standard and my revisionary account of thermodynamically reversible processes (lecture 2), it is essential that real processes can be brought arbitrarily close to the sequence of equilibrium states associated with a thermodynamically reversible process.
This condition of arbitrarily close approach by real processes fails at molecular scales. I will develop a "no-go" result that shows that, at molecular scales, attempts at thermodynamically reversible process cannot be brought to completion. They are disrupted by themal fluctuations and entropy creating irreversible processes must be employed to overcome them. The quantities of entropy that must be created exceed that tracked by Landauer's principle.
(Lecture 5) 2. Maxwell demons are in general poorly idealized as information processing machines.
Idealizing these demons as information processing machines has tangled us in a thicket of incomplete theory that is inadequate to the task. Our narrow focus on it has so distracted supporters and detractors of the information-theoretic approach that we have both overlooked an extremely simple and quite robust exorcism of Maxwell's demon that employs little more than a few elementary notions in statistical physics.
The exorcism proceeds by giving a simple description of what a Maxwell demon is supposed to achieve. It turns out that this description is incompatible with both a classical and quantum version of the Liouville theorem, which is one of the simplest results concerning the time development of classical Hamiltonian or quantum systems. There is no consideration of information, computation and memory erasure. One does noteven need to introduce the notion entropy.
Reading
John D. Norton, "All Shook Up: Fluctuations, Maxwell's Demon and the Thermodynamics of Computation" Entropy 2013, 15, 4432-4483
(Part II has the most recent and best developed version of the No-Go result. Part I, Section 4, has the new phase space based exorcism of Maxwell's demon.)
John D. Norton, "The Simplest Exorcism of Maxwell's Demon: The Quantum Version," http://philsci-archive.pitt.edu/10572/
John D. Norton, "When a Good Theory Meets a Bad Idealization: The Failure of the Thermodynamics of Computation." Goodies.
John D. Norton, "The Simplest Exorcism of Maxwell's Demon: No Information Needed," Goodies.
Background supplement: John D. Norton, "Brownian Computation is Thermodynamically Irreversible." Foundations of Physics. 43 (2013), pp 1384-1410. and "On Brownian Computation," International Journal of Modern Physics: Conference Series. 33 (2014), pp. 1460366-1 to 1460366-6.