Back to main course page

Assignment 4: Spacetime

For submission in Canvas
Canvas question may have different formats.

1. The figure shows the light cone of an event O in a Minkowski spacetime. Other events in spacetime can connect with O by various means.

(i) Some can receive light signals from O.
(ii) Some can send slower than light missiles to O.
(iii) Some can send light signals to O.
(iv) Some cannot exchanges any signals or missiles with O.
(v) Some can receive slower than light missiles from O.

Which of these events form:

(a) The surface of O's past light cone?
(b) The surface of O's future light cone?
(c) The interior of O's past light cone?
(d) The interior of O's future light cone?
(e) Outside O's light cone (both past and future)?

2. The spacetime diagrams show two events E₁ and E₂ in a Minkowski spacetime. Some show the worldline of an observer and that observer's hypersurface of simultaneity. Beware! Some are drawn incorrectly and do not properly represent a Minkowski spacetime.

Which shows:

(a) The worldline of an observer who judges events E₁ and E₂ to be simultaneous.
(b) The worldline of an observer who judges event E₁ to be earlier than event E₂.
(c) The worldline of an observer who judges event E₁ to be later than event E₂.

3. A tachyon propagates between the two events.

(a) Which corresponds to a tachyon propagating from event E₁ to E₂?
(b) Which corresponds to a tachyon propagating from event E₂ to E₁?
(c) Which corresponds to a tachyon connecting events E₁ and E₂ instantaneously?
(d) Which corresponds to the tachyon moving infinitely fast?
(e) Which corresponds to the tachyon moving slower than light?
(f) Which corresponds to the tachyon moving at the speed of light?

For discussion in the recitation

A. The relativity of simultaneity is revealed most simply in the following thought experiment in which two observers in relative motion judge the timing of two explosions by means the light signals they produce:

Draw a spacetime diagram of this experiment, indicating:

The planet observer's worldline and associated hypersurfaces of simultaneity.
The spaceship observer's worldline and associated hypersurfaces of simultaneity.
The worldlines of the front and rear of the spaceship.
The two explosion events.
The light signals emitted by the explosions.

The light postulate is an essential part of the above analysis that leads to the relativity of simultaneity. Just how does it figure in the analysis?

B. In a Newtonian space and time, the light postulate does not hold. Instead light conforms with an emission theory. That is, if light is emitted by a moving source, then the speed of the source is added to the speed of light (if the source moves in the direction of the light propagation); or subtracted from it (if the source moves in a direction opposite to that of the light propagation). Show that the above analysis does not yield the relativity of simultaneity if light conforms to an emission theory.

C. In the spacetime diagram below, two rods A and B approach one another from opposite directions.

(a) According to the judgments of simultaneity of the observer shown, the two rods have the same length: they coincide exactly when they pass by each other. Draw the observer's hypersurface of simultaneity for this moment and show that the observer will judge them to have the same length.

(b) Draw hypersurfaces of simultaneity for an observer who moves with rod A. Show that this observer will judge rod B to be shorter than rod A.

(c) Draw hypersurfaces of simultaneity for an observer who moves with rod B. Show that this observer will judge rod A to be shorter than rod B.

D. How does the analysis of C relate to the problem of the car in the garage?

E. At sunrise of Day 1, a monk commences a long walk up the narrow, winding road from the monastery in the valley to the mountain top. It is a hard, tiring climb, so he stops frequently to rest and even reverses his direction from time to time. He arrives at the mountain top just at the moment of sunset. At sunrise on Day 2, the monk commences the return journey. This time the journey is far easier. Rather than hurry to complete it quickly, the monk decides to pause frequently to admire the wildflowers, inhale the mountain air and absorb the splendor of the view. He arrives in the valley at the moment of sunset.

Is there any moment on the two days at which the monk is in exactly the same position on the road?

At first it seems impossible to determine an answer to this question from the information given. Whether there is such a moment seems to depend on the details of the monk's progress up and down the mountain. Drawing spacetime diagrams rapidly solves the problem, however. To see how, draw plausible world lines for the monk's two journeys on the spacetime diagrams here.

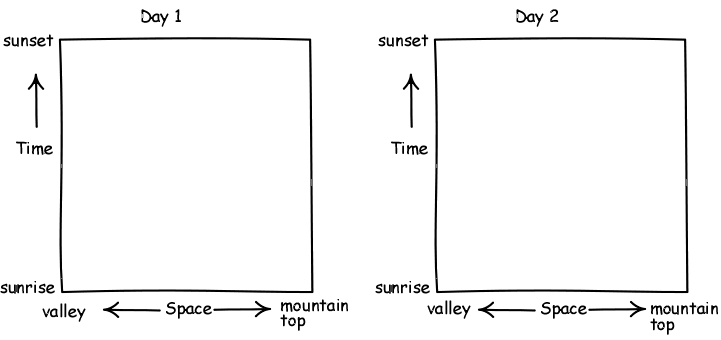
Explain how they make it obvious that the moment specified in the question must always exist no matter what the details of the monk's progress. (Hint: To see this, imagine the two spacetime diagrams superimposed.)