
Oxyrhynchus papyrus showing fragment of Euclid's Elements, AD 75-125 (estimated)
| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Here's an introductory puzzle. In the totality of our intellectual heritage, which book is most studied and most edited? The answer is obvious: the Bible. But which is the most studied and edited work after it? That is a little harder to say. The answer comes from a branch of science that we now take for granted, geometry. The work is Euclid's Elements. This is the work that codified geometry in antiquity. It was written by Euclid, who lived in the Greek city of Alexandria in Egypt around 300BC, where he founded a school of mathematics. Since 1482, there have been more than a thousand editions of Euclid's Elements printed. It has been the standard source for geometry for millennia. It is only in recent decades that we have started to separate geometry from Euclid. In living memory--my memory of high school--geometry was still taught using the development of Euclid: his definitions, axioms and postulates and his numbering of them.

Oxyrhynchus papyrus showing fragment of
Euclid's Elements, AD 75-125 (estimated)

Title page of Sir Henry Billingsley's first
English version of Euclid's Elements, 1570
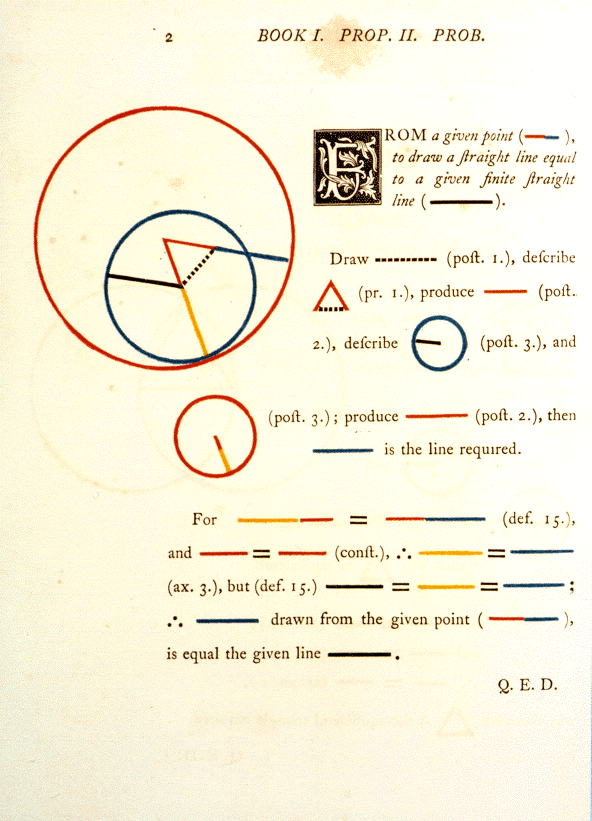
Oliver Byrne's 1847 edition of the first 6
books of Euclid's Elements used as little text as possible and
replaced labels by colors.

A recent edition from Dover.
This long history of one book reflects the immense importance of geometry in science. We now often think of physics as the science that leads the way. In the seventeenth century, Newton found one simple system of physics that worked for both the heavens and the earth. That set a standard of achievement that the other sciences sought to emulate. Newton, however, was learning from another science that already set an enduring standard of achievement: geometry.
We can identify two reasons for the importance of Euclid's Elements in our understanding of the foundations of science: its structure and the certitude of its results.
First, Euclid's Elements solved an important problem. When we have a large body of knowledge, such as we have in geometry, how are we to organize it? We know many simple things in geometry: the sum of the angles of a triangle are always 180 degrees. And we know more complicated things. A 3-4-5 sided triangle is a right angled triangle. And even more complicated things. As Pythagoras found, in a right angled triangle, the sum of the areas of the squares erected on the two shorter sides is equal in area to of a square erected on the hypotenuse.
So, as our knowledge grows, how are we to organize it so that we capture in it all the truths that we want and do not let in things that don't property belong there? Euclid employed a quite profound method, deductive systematization. His elements were structured according to a series of propositions:
All the definitions, axioms, postulates and propositions of Book I of Euclids Elements are here.
Once this structure is adopted, the problem of knowing just what really belongs in geometry is reduced to matters of deductive inference. Is this or that a truth of geometry? The question is answered by determining whether it can be deduced from Euclid's postulates and axioms. Do you doubt that this is a truth of geometry? Then you must show where Euclid's proof broke down. Eventually, as you trace the proof's back to their sources, you end up seeing that the truth of the result derives ultimately from the truth of postulates and axioms. And their truth is so obvious as to admit no doubt. Who wants to say that you cannot always draw a straight line between any two given points?
In the seventeenth century, with new-found confidence, natural philosophers rebuilt all learning from scratch, discarding the wisdom of antiquity as flawed. In that effusion of new investigation, one achievement stood unchallenged. That was Euclid's Elements. Indeed its premier position was reinforced when the structure it gave to geometrical knowledge was adopted by Newton to codify his new mechanics. Like Euclid, Newton listed definitions and, where Euclid gave axioms and postulates, Newton gave his celebrated three laws of motion. Euclid's Elements became the template for organizing knowledge, be it a new science such as Newton's or even knowledge outside science.
 |
 |
 |
 |
 |
 |
 |
 |
 This figure (from the Latin first edition) is part of Newton's demonstration of Kepler's second law. A body moving under a force directed to a point moves such that a radial line to the point sweeps out equal areas in equal times. |
 This figure (from the Latin first edition) is part of Newton's demonstration that a planet that orbits in an ellipse is attracted to the a central point by a force that varies in intensity with the inverse square of distance. |
Second, the enduring success of Euclid's Elements assured us that some things could be known with certainty. While the knowledge of antiquity collapsed, geometry thrived as the method central to Newton's discovery and also the template for his organization of his new mechanics. The idea of that sort of certainty is familiar today. We are used to the idea that some branches of study do not need fragile experiments to verify them. There is no point in counting two apples and then two apples into a basket to verify that 2+2=4; and then doing it again with pears or pineapples, just to be sure. Arithmetic does not need it. 2+2 does not just happen to be 4; it has to be 4. There is no other possibility.
So Euclid's geometry and Newton's physics bequeathed to thinkers the problem of understanding just how this level of certainty was possible. Our modern minds are steeped in the idea that knowledge of the world comes from experience and that new experience can always overthrown old learning. By the eighteenth century, the sense was widespread that Euclid and Newton had found the final truths of geometry and mechanics.
 |
The philosophical problem was to determine how
this was possible. In the eighteenth century, the problem was posed
most sharply by David Hume. We have the
experience that fire has always burnt us and bread always nourished
us, he noted. But from that we can derive no assurance that fire
will in the future burn us and bread nourish us. We suppose it as a
matter of habit that, so far, has not misled us. This was a conundrum. We knew the final truths about the geometry of space and dynamics of bodies. However our epistemic means, that is, the ways we had of ascertaining truths, were too limited in their reach to provide this certainty. |

Immanuel Kant
One of the most influential thinkers of all time, the eighteenth century philosopher Immanuel Kant, was awakened by Hume from his "dogmatic slumbers" and provided an enduring answer. There are some types of knowledge that are both synthetic and a priori, he declared. They are synthetic in the sense that they say more of their subjects than are given by the subject's definition; they are a priori in the sense that they can be know prior to experience of the subject. Arithmetic and geometry were Kant's premier examples of synthetic a priori knowledge. According to Kant, it is a synthetic, a priori truth that 7+5=12; and it is a synthetic, a priori truth that the sum of the angles of all triangles is 180 degrees, that is, two right angles.
Count the sides: 1, 2, 3. "A triangle has three sides." ... is analytic, since the definition of triangle includes the idea that it has three sides. |
A + B + C = 180 degrees = two right angles "A triangle's angles sum to 180 degrees." ... is synthetic, since this summation to 180 degrees is not part of the definition of a triangle. It is an addition. |
| This proposition is known a priori. That is, its truth is know to us prior to any experience of triangles. the definition of a triangle assures us every triangle we meet has three sides. If it does not, it is not a triangle. | Since this proposition is synthetic, one might think that its
truth can only be determined by finding many triangles, measuring
their angles and checking that they sum to 180 degrees. That is, its
truth can only be known a posteriori,
that is after experience. Kant's observation, however, was that we did not need to go through this exercise. For any reader of Euclid's Elements would be sure, before any measurement of real triangles, that the sum must be 180 degrees. That is, the proposition was a synthetic, a priori truth. Kant's account of how such propositions are possible was ingenious and tendentious. He urged that, in our interactions with the world, our apparatus of perception imposes certain regularities on our perceptions and we can be sure that all our our perceptions will have them. These regularities include the synthetic, a priori truths of geometry. This is not the end of this story. We shall see shortly that Einstein disagreed. |
These ideas provide our starting point. We shall see in
later chapters that matters take a very different turn in the nineteenth
century.
Nineteenth century mathematicians realized that the eighteenth century
certainty of geometry was mistaken. Geometry was an empirical science. It
reported the way our space happened to to be, not the way it had to be. If
that was so, other geometries were possible
and our experience of space might well have been different. In the
nineteenth century, these were regarded as possibilities that were
unrealized. Nature had many choices but, they thought, she chose Euclid's
system.
This realization of the mere possibility of geometries other than Euclid's was shocking. Greater shocks were in store. In the twentieth century, Einstein delivered the final insult to Euclid. He found through his general theory of relativity that a non-Euclidean geometry is not just a possibility that Nature happens not to use. In the presence of strong gravitational fields, Nature chooses these geometries.
Copyright John D. Norton. December 28,
2006, February 28, 2007; February 2, 9, 14, September 22, 2008; February
2, 2010; January 1, 2013. February 13, 14, 2017. January 30, 2022. February 13, 2024.