























| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Let us take stock and summarize what we shall need as we move towards Einstein's general theory of relativity.
In the last few chapters, we explored one of the most important episodes in the history of science. Geometry is one of our earliest and best developed sciences. By the eighteenth century, its results were so familiar and so reliable that we came to believe that geometry had to be just as Euclid has said.
That 5+7=12 is a truth of arithmetic. We do not need to do experiments to show it. We can, if we like, put 5 pennies and then 7 pennies in a jar and count how many are there overall. There will be 12. Or we can, if we like, put 5 apples in a basket and then add in 7 more and count how many are there overall. There will be 12.
     |
+ |        |
= |             |
We could do this, but we know it is unnecessary. 7+5 has to be 12. It is just a necessity of arithmetic. We have
7 = 1 + 1 + 1 + 1 + 1 + 1 + 1
5 = 1 + 1 + 1 + 1 + 1
12 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
In the eighteenth century, it was thought that geometry was the same. We could measure the angles of a large triangle of tightly stretched ropes, spread out in some paddock, and sum the results. We would find they sum to 180 degrees. We could go out and measure the circumference of a circle of rope. We would find that is it π times the diameter. We could do these measurements, but they are unnecessary, it was thought. The results have to be as stated.
For example, we could carefully draw the most famous of all right angled triangles, a 3-4-5 sided triangle, on a large piece of paper. To draw it, we enclose a right angle with straight lines of length 3 and 4. We can then form a triangle by connecting the ends of the side. We could then check that its hypotenuse really is length 5 by measuring the sides with a ruler.
Once again, actually performing the measurement is superfluous. We know from Pythagoras' theorem that the hypotenuse has to be 5 units in length. This just follows from Pythagoras' sum of squares rule that relates the lengths of the three sides. It just looks like more arithmetic.
52 = 32 + 42
25 = 9 + 16
All this changed. The great discovery of the nineteenth century was that this was not so. Other geometries were quite possible and it was a matter of empirical investigation to find out which geometry holds of our space. We were already well advanced in those investigations. We had found that Euclidean geometry holds as long as we look at smaller parts of space. But we could not preclude deviations from Euclid's geometry if we surveyed very large volumes of space. Since no one had done it, we could not know what would result.
The simplest deviations from Euclid's geometry would come through the failure of his fifth postulate. That postulate 5ONE, you will recall, demands that just ONE straight line can be drawn parallel to a given straight line, through some point not on the line. There are two alternative postulates, each generating a different geometry. One, 5NONE, asserts that there are NO straight lines parallel to the given line. The other, 5MORE, asserts that there are MORE than one straight lines parallel to the given straight line, through the one point.
Postulate 5ONE
Postulate 5NONE
Postulate 5MORE
If one is familiar with Euclidean geometry, that will seem very odd, initially. How could the sum of the angles of a triangle be anything other than 180 degrees? We can get a sense of how this can be by imagining that we set out to survey the geometry that applies to a large curved surface, such as the spherical surface of the earth.
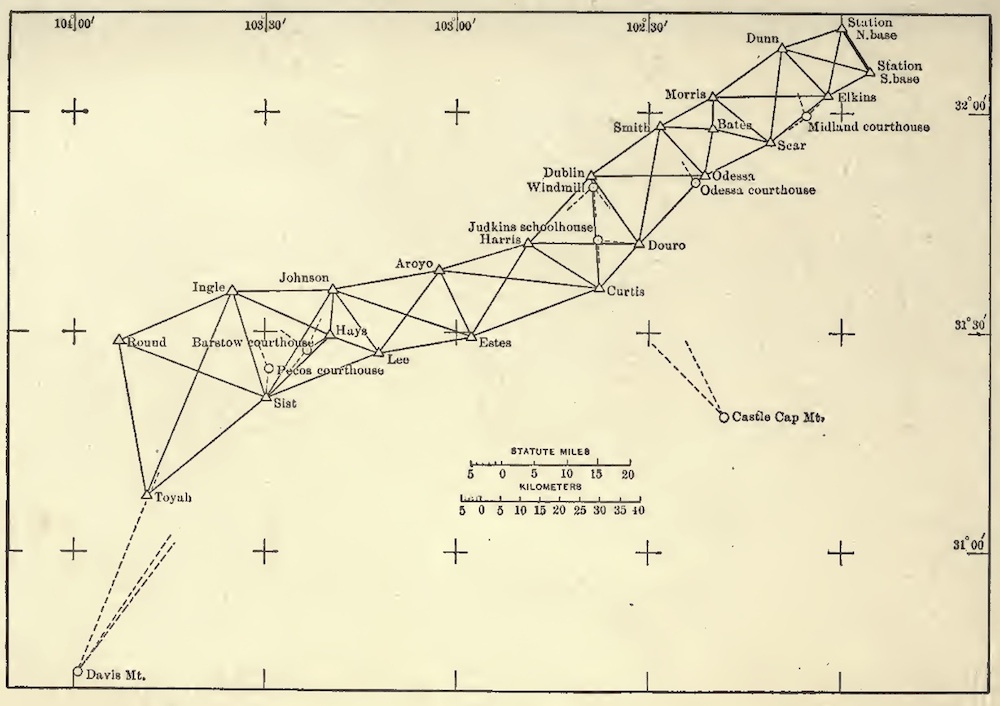
Map of geodetic survey from E. R. Carey,
Geodetic Surveying. New York Wiley, 1916, p. 5.
http://archive.org/details/geodeticsurveyin00caryrich
Our surveying efforts would yield familiar Euclidean results, as long as they are confined to a small portion of the earth's surface. Triangles will have angles that sum to 180 degrees. That would be so, near enough, for the triangle A''B''C'' below.
However, as we explore larger areas, deviations will creep into our results. The triangle A'B'C' will have angles that sum to more than 180 degrees. The largest triangle shown, ABC, will have angles that sum to 270 degrees. Other familiar results of Euclidean geometry will fail in ways described in the last chapter. They need not be repeated here.
One idea from that chapter is so important that it does bear repetition. Just what do we mean by a "straight line" in this geometry, such as might be the side of one of these triangles? We mean by it a path of shortest length, that is, a "geodesic."
The geometry of the surface of a sphere is the geometry of a surface with constant curvature: the surface of a sphere has the same curvature everywhere. It is positive curvature since two geodesics at right angles curve in the same direction in the space. This is the geometry associated with the alternative postulate 5NONE.
There is a second case of a surface of constant curvature, described also in the last chapter. This is a surface of negative curvature. Two geodesics at right angles curve in opposite directions in the space. The surface is like that of a saddle. When triangles grow large on this surface, the sum of their angles is less that 180 degrees. This is the geometry associated with the alternative postulate 5MORE.
So far, we have explored the geometries of 5NONE
and 5MORE for the case of two dimensional spaces. We can also
consider each in three dimensional spaces. The results we would arrive at
are summarized in the table (duplicated in Euclid's
Postulates and Some Non_Euclidean Alternatives).
| Spherical Geometry Positive curvature Postulate 5NONE |
Euclidean Geometry Flat Euclid's Postulate 5ONE |
Hyperbolic Geometry Negative Curvature Postulate 5MORE |
|
| Straight lines |
Finite length; connect back onto
themselves |
Infinite length |
Infinite length |
|
Sum of angles of a triangle |
More than 2 right angles |
2 right angles |
Less than 2 right angles |
|
Circumference of a circle |
Less than 2π times radius |
2π times radius |
More than 2π times radius |
|
Area of a circle |
Less than π(radius)2 |
π(radius)2 |
More than π(radius)2 |
|
Surface area of a sphere |
Less than 4π(radius)2 |
4π(radius)2 |
More than 4π(radius)2 |
|
Volume of a sphere |
Less than 4π/3(radius)3 |
4π/3(radius)3 |
More than 4π/3(radius)3 |
In very small regions of space, the three geometries are
indistinguishable. For small triangles, the sum of the angles is very
close to 2 right angles in both spherical and hyperbolic geometries.
What made visualizing these non-Euclidean geometries easy was that we embedded the non-Euclidean space in a higher dimensioned Euclidean space. That took an unfamiliar and even disquieting geometry and made it familiar. However in the end, we must dispense with these higher dimensional embedding spaces and simply take the new geometries as worthy geometries in their own right. There are three problems if we do not dispense with the embedding space.
| 1. The first is technical. Sometimes the embedding cannot be implemented fully. The two dimensional negatively curved saddle shape can only be embedded into a three dimensional space in pieces; the full surface cannot be embedded. |
2. The second is practical. The real gain is supposed to be to our imagination. Imagine a three dimensional curved space that is curving into the fourth dimension of a four-dimensional Euclidean space. Well--that's the problem. You cannot imagine it. The practical gain to visualization is lost in this case. It is replace by a new problem: how are we to visualize the curving of the three dimensional space into a four dimensional space?
To get a sense of how much our imagination is taxed by visualizing a fourth dimension, here is how we might try to understand what a four-dimensional cube looks like. We cannot see the totality of a four-dimensional cube. The best we can do is to build a three-dimensional picture of one. To figure out how to do that, we recall how we might draw a two-dimensional picture of a three-dimensional cube. We draw two opposing faces and connect the corners.
To get the three-dimensional picture of a four-dimensional cube, we start with two opposing faces. They are three-dimensional cubes. We then connect the edges. This is the result.
For more details, see the chapter What is a four dimensional space like?"
3. The final problem is the most serious. If our geometry turns out to be factually one of the curved geometries, then the supposition of a higher dimensioned Euclidean space is a falsehood and a potentially very misleading one. For, if we take it seriously, we end up believing that space is really Euclidean after all, but only in some higher dimension to which we have no access. If all we know is the three dimensions of space in which we measure, then we have no license to conjure up an otherwise inaccessible higher dimensioned Euclidean space for it to curve into. What makes us think such a higher dimensioned space exists?

Copyright John D. Norton. December 28, 2006, February 28, 2007; February 2, 9, 14, September 22, 2008; February 3, March 1, 2010; January 1, 2013; February 15, 2015. February 16, 2022. February 15, October 2, 2024.