| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Linked document: Two
Spaceship Tachyon Paradox
Once we have the notion of spacetime and the simple picture it brings of the relativity of simultaneity, we find that other processes and effects in special relativity become much easier to understand. Here is a collection of a few of them.
One of the most intriguing entities in relativity theory are tachyons. They are hypothetical particles that travel faster than light. They are distinguished from "bradyons," particles that travel at less than the speed of light. While bradyons are familiar and include protons, electrons and neutrons, tachyons have never been observed.
| Bradyons | Tachyons |
| travel slower than light | travel faster than light |
| ordinary matter | exotic matter (not found) |
| Add energy and momentum and they speed up. |
Add energy and momentum and they slow down. |
| c is the upper limit to their speeds | c is the lower limit to their
speeds |
For present purposes, the interesting fact is a curious property: for some observers tachyons travel backwards in time. With the spacetime representation of the relativity of simultaneity, it is now easy to see how this comes about. The figures below show a tachyon being created and propagating into space; and how three different observers would judge the same process of tachyon creation.
| Observer A judges the tachyon to be moving forward in time from its creation at the instant marked "now." It propagates from the "now" hypersurface of simultaneity towards the "later" hypersurface of simultaneity. |
| Observer B moves in the direction of propagation of the tachyon. Observer B finds the tachyon to lie fully within one of B's hypersurfaces of simultaneity, the "now" hypersurface that contains the event of the tachyon's creation. Indeed the "now" hypersurface contains all the events in the tachyon's history. So the tachyon exists only "now" for observer B. That is, for B, the tachyon has infinite speed--it covers distance in no time--and it has disappeared to spatial infinity in the same instant "now." |
| Finally observer C, who moves even faster in the same direction, judges the tachyon to be traveling into the past. The tachyon is created on the "now" hypersurface of simultaneity and propagates towards the "earlier" hypersurface of simultaneity. It arrives at the earlier hypersurface that collects events from an earlier time before it was created. That means that the tachyon is traveling backwards in time. |
| All three figures above are drawn
with the tachyon moving up the page. So it is easy to fall into the
trap of imagining that the figure with observer A shows what is
really happening: that the tachyon is really propagating forwards in
time and that the other two figures represent distorted reporting
from observers B and C in motion. That is not how it works. The
principle of relativity assures us that the reports of all of the observers
are equally good. C's reporting of the tachyon traveling
backwards in time is as good as A's reporting of the tachyon
traveling forwards in time. That the figure showing observer A looks
more natural is just an accident of the way the figures have been
drawn. We could equally well draw the figures so that C's worldline
is vertical. Then, as shown at left, the natural reading would be
that the tachyon propagates backwards in time. None of the figures is any more correct than any other. The principle of relativity assures us that all the observers are equally good. Since they disagree on whether the tachyon propagates forwards in time, the best we can say is that there is no observer independent fact of the direction of propagation, just as there is no fact as to which observer is really at rest. |
For some observers, tachyons travel backwards in time, that is, into the past. Does that mean that they can be used to affect the past, that is, to change the past? Does that mean that we can use them to create paradoxical situations?
The standard time travel paradox is the one in which a time traveler travels back in time and kills his or her grandfather; so that the time traveler is never born; so the time traveler doesn't travel back in time! This closed loop produces a contradiction. The time traveler both exists at some time and and does not exist at the same time.

Public domain http://en.wikipedia.org/wiki/File:Moordwillemzwijger2.jpg
It proves to be quite easy to conceive situations in which tachyons are emitted and absorbed in such a way as to produce similar closed, paradoxical cycles. A simple tachyonic paradox employs a single spaceship that is run entirely by robots. The robots have been programmed to steer the spaceship along a precise path, to emit a tachyon at a precise moment in a precisely specified way and to react to the reception of a tachyon in a specific way. All this is planned so that the following interactions are possible.
| The spaceship passes uneventfully though its position at time 1 to its position at time 2. Then it is programmed to emit a tachyon into the past that will strike a tachyon mirror, placed ahead in a pre-arranged location. The mirror is oriented so that the reflected tachyon will continue propagating into the past such that its path intersects with the spaceship at the earlier time 1. | |
| The spaceship is equipped with a tachyon
detector. If the detector detects a tachyon, it is programmed
to destroy the spaceship. |
|
| The spaceship detects the tachyon at time 1 and destroys the spaceship. Thus there is no spaceship at later time 2 to emit a tachyon. | |
| At time 1, the spaceship does NOT receive a tachyon, so the robots do NOT destroy the spaceship. | |
| The spaceship survives to time 2,
whereupon is DOES emit a tachyon into
the past that propagates towards the spaceship at time 1. And so on ... |
|
| See these frames
animated. |
This thought experiment conforms with the International Thought Experiment Code of Conduct. No imaginary humans or imaginary animals were thought to be harmed. |
The spacetime diagram above simplifies the spaceship and mirror motions needed to implement the paradox. For the spaceship to judge the emission of the tachyon as propagating from the spaceship towards the mirror, the spaceship would need to adopt briefly a rapid motion of recession away from the mirror. To judge the arrival of the tachyon as propagating from the mirror, the spaceship would need to adopt briefly a rapid motion towards the the mirror. The mirror itself would (plausibly) not be a simple silvered surface. It would be an active device that similarly changes its states of motion so that it judges a tachyon as received from the spaceship and then, adopting a different state of motion, a tachyon emitted towards the spaceship.
Summarizing, we have arrived at the following inferences:
| Spaceship does NOT receive a tachyon at time 1. | 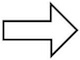 |
Spaceship survives to time 2 and emits a tachyon. |  |
Spaceship DOES receive a tachyon at time 1. |
| Spaceship DOES receive a tachyon at time 1. |  |
Spaceship does not survive to time 2. No tachyon is emitted. |  |
Spaceship does NOT receive a tachyon at time 1. |
We have a contradiction:
| Spaceship does NOT receive a tachyon at time 1. | if
and only if |
Spaceship DOES receive a tachyon at time 1. |
If you know a little logic, you will find it easy from this to infer to a contradiction in the traditional form: (Tachyon IS received AND tachyon is NOT received.)
This is the simplest tachyon paradox. It assumes that
there is such a thing as a tachyon mirror. Here is a more
complicated version that employs two spaceships and does not
assume that there are tachyon mirrors.
Two Spaceship Tachyon Paradox
Since tachyons are candidates for serious science and not imaginings of science fiction, we cannot tolerate such an outright contradiction. Somehow it must be resolved. The most obvious resolution is the most severe. We could just suppose that these paradoxes show that there are no tachyons. What gives this escape strength is that we have, so far, never found tachyons.
Nonetheless, this resolutions seems too severe to me. It risks elevating something that just happens to be the case (there happen not to be tachyons) to something that has to be the case (there cannot be tachyons). Other weaker resolutions are possible.
| The simplest resolution is just to suppose that
the emission of tachyons is just not something
that can be controlled by us. Just as the receipt of a
signal is something that happens to us, the emission (or receipt) of
a tachyon is again just something that happens to us. We cannot
choose to receive a tachyon when there is none there.
Correspondingly we cannot choose to emit a tachyon. An emission
might just happen. The paradox above depends on the robots being able to emit a tachyon when their programming calls for it. If that is no longer possible, we might suppose that tachyonic interactions are limited to ones that involve no paradoxical contradictions. What makes this resolution plausible is that there is no absolute distinction between the emission and receipt of a tachyon. What one observer counts as an emission, another may count as a receipt. So we might expect the one rule of lack of control to cover both emission and receipt. |
We can make this resolution a little more precise
by asking for more details of the tachyons. So far, we have just
posited tachyons and explored how they must behave in virtue of the
background spacetime in which they live. A more
complete theory of tachyons has to provide a fuller theory
of what they are. We have taken a similar short cut with light signals. We just assume that light signals can be created at will by us and detected as needed. We can do that since we have a full theory of light. We know that we can create light by, for example, discharging a high voltage through a gas. We know that we can detect light through its effects on silver halides in a photographic emulsion; or, in more modern technology, through the voltage it creates in a photodiode. Can there be a similar, well-developed theory of tachyonic matter that allows us to create tachyons and detect them with similar facility? The tachyon paradox shows that no tachyon theory of this type can be consistent. |
| Consider again observer
C from earlier. We described observer C as finding a
tachyon emission event in C's "now" time and that the tachyon is
emitted into the past. We might imagine that C hit a trigger on some tachyon creation device that led to the emission. However C's normal description of the process would be quite unlike that of an emission that C brought about. Rather, C would say that, at an earlier time, there was a tachyon propagating towards C. It arrived at the moment that C hit the trigger on the device. The arrival of the tachyon and the hitting of the trigger just fortuitously coincide. |
We could look to other more fanciful resolutions. Perhaps tachyons exist but they do not interact with normal matter. Neutrinos are almost like this. They flood through us, but interact so rarely with us that only the most sophisticated instrumentation can detect them. We might suppose that tachyons are like neutrinos, except it is not that they almost never interact with us. They just never interact with us.
This escape is dubious. If tachyons never interact with us, we can never know they are there. We are reminded of the ether state of rest of 19th century electrodynamics. It is there, we were assured, but the theory precluded us ever knowing which state of motion coincided with it. Both look like something nonexistent whose supposition of existence is protected by artful theoretical contrivance.
A curious fact mentioned above is that adding energy and momentum to a tachyon leads it to slow down; and, as we add arbitrary amounts of energy and momentum, the tachyon speed slows arbitrarily close to the speed of light. This is the opposite of what we expect. Adding energy and momentum to ordinary massive particles like neutrons, protons and electrons leads them move faster with an upper limit of the speed of light.
The most direct way to see the effect is just to write down the formulae for energy and momentum of a tachyon and see what happens when we change the tachyon's speed. Details here. We can, however, see a closely related kinematical effect, which gives a sense of why the slowing down occurs. The effect shows that the slowing of tachyon is closely related to the relativity of simultaneity and how the hypersurfaces of simultaneity tilt as we alter the inertial frame of reference.
| The spacetime diagram shows a massive particle that moves inertially from event O to event A in unit time. The diagram is drawn so that the worldlines of the rest frame of the particle are vertical. The diagram also shows a tachyon that moves at infinite speed between two events O and B that are unit distance apart and happen at the same moment of time according to the judgments of simultaneity of the frame of reference shown. The speed of light is unity in this figure, since the light cone, shown as a dashed line, traces a light signal that covers unit distance in unit time. |
| How would the particle and tachyon behave if we were to set the pair of them into motion at half the speed of light? We can answer simply by shifting our reporting to an inertial frame of reference that recedes from them at half the speed of light, as shown on the left. The massive particle will be moving at 1/2 the speed of light in this frame. We can read that speed from the times and distances shown. The particle covers 1/2 a unit of distance in unit time. (To draw the figure, we locate the event A in the figure using the earlier results on clock slowing. The unit proper time elapsed in the particle's motion will register as 1.15 units of time in the new frame of reference.) |
| The tachyon trajectory will be as shown in the figure on the right, using the fact that the transformation between inertial frames of reference is symmetric around the light cone, shown as the dashed line. The trajectory OB lies on a hypersurface of simultaneity in the rest frame of the massive particle. That hypersurface is tilted up toward the light cone in the new frame of refence. That is where the tachyon trajectory OB lies in the new diagram. The most important result is that the tachyon now propagates from the event O to the event B in non-zero time. That is, it covers unit distance in half a unit of time. Since 1/(1/2) = 2, its speed is 2, which is twice the speed of light. The tachyon has slowed down. |
The process just described is one that leads massive particles to speed up and tachyons to slow down. That is a purely kinematical effect. We know from a dynamical analyses elsewhere that the speeding up of the massive particle coincides with it gaining energy and momentum. We need to go outside the analysis of these figures to affirm that the same thing has happened to the slowed tachyon: its energy and momentum has similarly increased. The result is surely not surprising. For those who want the details, here is a demonstration.
| So far we have considered how the particle and tachyon manifest in a frame of reference that recedes from them at half the speed of light. It should be evident now that, as we proceed to inertial frames of reference that recede even faster, the massive particle will be sped up more and the tachyon will be slowed down more. Both will end up moving closer and closer to the speed of light, while never actually attaining that speed. The figure on the left shows the particle and tachyon in a frame of reference that recedes from them at 3/4 the speed of light. |
That inertial observers in relative motion will each judge the others' clocks to run slower is, by now, a quite familiar and readily understandable outcome of relativity theory. It does take a little while to get used to the idea, of course. When you first hear it, it seems strange and even paradoxical. How can each be correct in judging the other's clock to have slowed? What would happen if the two observers meet and compare their clocks? If relativity is right, each would have to read a time earlier than other; and surely that is impossible. Or is it?
We now know that these concerns are misplaced. The clocks cannot start out from the same place and then be re-united without one or both accelerating; and those accelerations so interfere with the analysis that no contradiction arises. When either accelerates, they cease to be inertial observers.

However an enduring literature has tried to generate some
sort of paradox from the effect of relativistic clock slowing. The most
famous of the these attempts is associated with a story of two twins. One
stays on the earth--the "stay-at home-twin." The stay-at-home
twin's motion is inertial throughout. The other travels off rapidly into
space, journeys far and fast and then returns home. The traveling twin
must accelerate to complete this journey.
The story of what happens is readily told from the point of view of the stay-at-home twin. The traveling twin's clocks will slow due to the twin's rapid motion. That slowing encompasses all processes related to time. So the traveling twin's metabolism will slow as well. When the traveling twin returns to earth, the traveler will have aged significantly less. If the traveling twin had maintained a speed of 86.6% the speed of light, the internal clock would slow to 50% of the normal rate. Let us say the traveling twin returns, after what the stay-at-home twin finds to be 8 days. The traveling twin will experience merely the passing of 4 days.
| All this can be depicted in a simple
spacetime diagram. It shows the
worldline of the stay-at-home twin. The numbers 1, 2, ... , 8 are
the days of time elapsed on the stay-at-home twin's clock. It also
shows the worldline of the traveling twin, who moves away from
earth, travels inertially for four days of stay-at-home twin time;
abruptly turns around; and then takes another 4 days to return.
Because the traveling twin is moving so fast, the traveler's clock
and the traveling twin's metabolism run at half the speed of the
stay-at-home twin. The numbers 1, 2, 3, 4 represent the days of time
elapsed on the traveling twin's clock and metabolism. The twins have set their clocks to zero at the start when the traveling twin leaves. When the traveling twin returns, the stay-at-home twin has aged 8 days, but the traveler has aged only 4 days. So far, the analysis is straightforward. Where the problems enter, is if we try to recount the story from the perspective of the traveling twin--and do it badly. The temptation is to say that, from the traveling twin's perspective, everything looks the same. The stay-at-home twin recedes, then turns around and comes back. So, we are tempted to ask, should the stay-at-home twin have aged less? Since the stay-at-home twin cannot have both aged more and less, do we have a paradox--often called the "twin paradox"? We should not expect the stay-at-home twin to age less. The error made was to assume a symmetry in the two twins. The stay-at-home twin maintains inertial motion throughout the process. The traveling twin must at some point turn around and return. Even if very briefly, the traveling twin must accelerate. That acceleration makes a big difference and enables us to maintain different results for each twin. |
| Relativity theory is able to give a
consistent account of times elapsed for both twins. The clearest
account shows the judgments of simultaneity made by each twin. First, the diagram opposite shows the judgments of simultaneity of the stay-at-home twin. As time passes on the clock of the stay-at-home twin, we can trace out the corresponding times on the clock of the traveling twin. The two clocks are both set to 0 at the outset. Then, the traveler's clock starts to lag. After 2 days have elapsed for the stay-at-home twin, we follow the hypersurface of simultaneity from the worldline of the stay-at-home twin to the traveling twin to find that just one day has elapsed for the traveler. Repeating for the remaining times, we see that for each time elapsed on the stay-at-home twin's clock--2, 4, 6, 8 days--half the time has elapsed on the traveling twin's clock--1, 2, 3, 4. |
|
Now consider the judgments of simultaneity
of the traveling twin, as shown in the spacetime diagram
opposite. Since the traveling twin is moving very rapidly, the
traveler's hypersurfaces of simultaneity are quite tilted. |
Careful attention to the differing judgments of simultaneity of the two twins shows that there is nothing paradoxical in the twin effect. The brief moment of acceleration of the traveling twin completely alters the traveler's judgments of simultaneity and this alteration is key to seeing how relativity provides a consistent account of the effect.
Nevertheless, many still get confused by the twin effect.
The traps they fall into go something like this.
Question: If the stay-at-home twin judges the other
twin's clock to slow, does not the principle of relativity require that
the traveling twin see the same thing for the stay-at-home twin?
Otherwise, could we not use the difference to detect the absolute motion
of the traveling twin?
Answer: The principle of relativity applies to inertial motion.
Only the stay-at-home twin moves inertially. So the principle of
relativity is applied to that twin only. There is no problem in the
traveling twin deciding that he is moving from the relative slowing of his
clock, since what he is really inferring is that he is accelerating.
Question: OK--forget the principle of relativity.
Is there not a symmetry in the situation. Each sees the other moving so if
one sees the other's clock slow, should not both?
Answer: There is not a perfect symmetry in the two twins. One moves
inertially; the other accelerates. So there is no basis for expecting
symmetrical effects and we do not get them.
The reason I have gone into such detail on the story of
the twin effect is that it turns out to be especially simple to understand
when we relate it to the geometry of a Minkowski spacetime.
The result that will interest us is one of the most fundamental results of
Euclidean geometry, that is, of the ordinary
geometry of our space. If one has two points in space, which of all
possible curves is the straight line the connects them? The answer is that
the straightest is the shortest.
| This shortest
curve is called a "geodesic." That the straight lines are
the shortest is a very familiar fact of experience. If I need to go
from one side a large hall to another quickly, I choose the straight
path since that is the shortest. The figure shows a straight line as
the shortest curve connecting two events A and B. |
There is an analogous notion in
Minkowski spacetime (and in all relativistic spacetimes). Think
of all the timelike trajectories that might represent the motion of some
physical system. How do we distinguish those that are inertial? In the
spacetime diagrams, they are drawn as straight lines since they are
straight in several senses. The one that matters to us here is that they
are geodesics analogous to the geodesics of Euclidean geometry.
In a Euclidean space, every curve has a length. If we
drive a car on some trip, the length of the road we traverse is measured
by the car's odometer. In spacetime there is a similar notion. As you or I
traverse some timelike worldline in spacetime, we carry an instrument that
measures the curve's "length" in spacetime, analogous to the car's
odometer. That instrument is our wristwatch or any other clock we carry
with us. The length of a timelike curve in
spacetime is just the time elapsed as read by a co-moving clock.
So now we can say which of all timelike trajectories connecting two event A and B in a Minkowski spacetime is the inertial trajectory. It is just the timelike geodesic, where: Timelike geodesic: The timelike curve connecting two events of greatest proper time.
| The definition is exactly
like that of the geodesic of Euclidean space, except that
we have replaced shortest spatial length by greatest
proper time. It tells us that we proceed from event A to event B
with greatest elapsed time if we follow an inertial trajectory. |
But that fact is just the result of the
twin
effect! The stay-at-home twin travels to some event in his future
along an inertial trajectory. The traveling twin follows an accelerated
trajectory along which less proper time elapses.
So we see that the twin effect is as fundamental to the geometry of a Minkowski spacetime as is the simple idea in ordinary geometry that a straight line is the shortest distance between two points.
Special relativity requires us to believe something that at first seems unbelievable: that two inertial observers in relative motion will judge the same speed for the same light signal. We know now that the relativity of simultaneity solves the problem. The two can judge the same speed for light since, through the relativity of simultaneity, they set the clocks used to measure the speed of light differently.
Visualizing just how the relativity of simultaneity enables the light postulate to hold for all inertial observers is not easy as long as we try to picture things in ordinary space. It does become dramatically simpler once we depict them in spacetime and use the simple geometric picture of the relativity of simultaneity that it affords.
To see how this comes about, let us first sharpen the problem by describing the difficulty in a quite concrete case. Once we see how the relativity of simultaneity resolves this one case, others are obviously analogous. Imagine that we have an inertially moving rod and a light signal that bounces back and forth between its two ends.
For a observer at rest on the rod, the light signal will take the same time for the forward and return journey.
| Now imagine that we redescribe the process from the perspective of an observer on a nearby planet, who judges the rod to be in uniform motion along its length. That planet observer would judge the light to need more time to traverse the rod in the direction of the rod's motion and less in the direction opposite to rod's motion. | Remember how it goes? When the light signal moves in the direction of the rod, it chases after a fleeing end and needs more time to catch it. When the light signal moves in the opposite direction, its destination is an end that approaches; so it needs less time to reach it. Note that the speed of light is assumed to be the same in both directions. |
If the light postulate is to hold for both inertial observers, somehow both have to be right. The forward the return journal should take the same time for the rod observer; and they should take different times for the planet observer.
Let's now look at the spacetime diagrams for this process.
| First here's a spacetime diagram that
depicts the rod observer's judgments.
In particular, the hypersurfaces of simultaneity reflect the rod
observer's judgments of simultaneity of events.
The equal spacing of the hypersurfaces reflects the rod observer's judgment that equal times are needed for the forward and return journey of the light signal. More precisely, the events in question are the arrivals of the light signal at either end of the rod. The hypersurfaces reflect how the rod observer associates these events with events simultaneous with them on the rod observer's own world line. The rod observer will then use a single clock carried with the observer to judge the equality of times elapsed between these latter events. |
| Here's the spacetime diagram that
depicts the planet observer's judgments.
In particular, the hypersurfaces of simultaneity reflect the
judgments of simultaneity of events by the planet observer.
It is clear that a greater time is needed for the light to traverse the rod when the light propagates in the direction of the rod's motion; and less time is needed for the return trip. The speed of light in both directions remains the same. That is captured by the fact that the lightlike curves in both directions are at 45o to the vertical. |
| How can both views cohere? That
becomes apparent immediately if we now depict how the planet
observer judges the rod observer's hypersurfaces of simultaneity to
be spread over the spacetime.
The planet observer notices that the rod observer's judgments of simultaneity differ from the planet observer's. The difference lies in a tilting of the rod observer's hypersurfaces of simultaneity. Indeed that tilting is precisely what is needed to restore the equality of times for the forward and return trips of the light signal. |
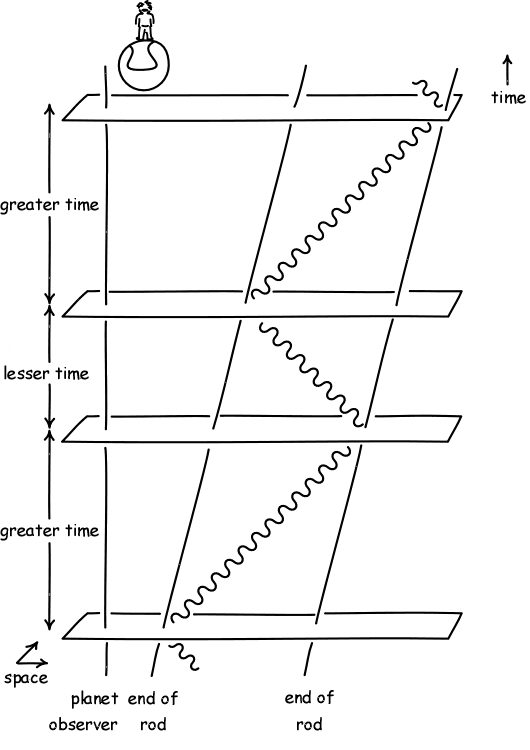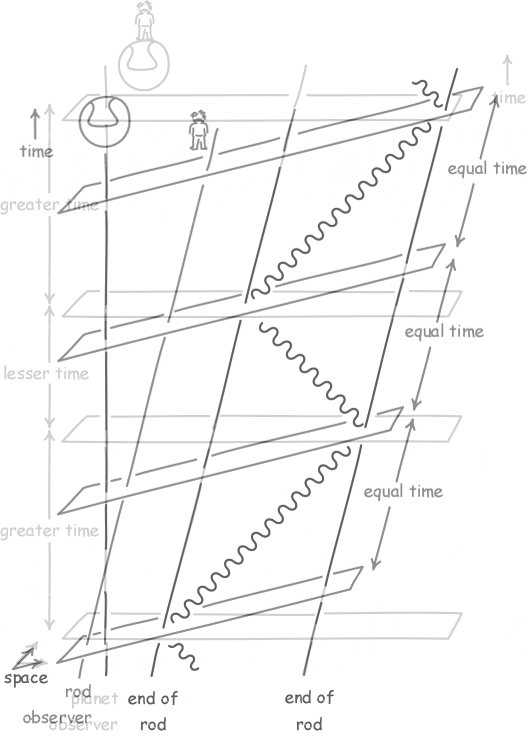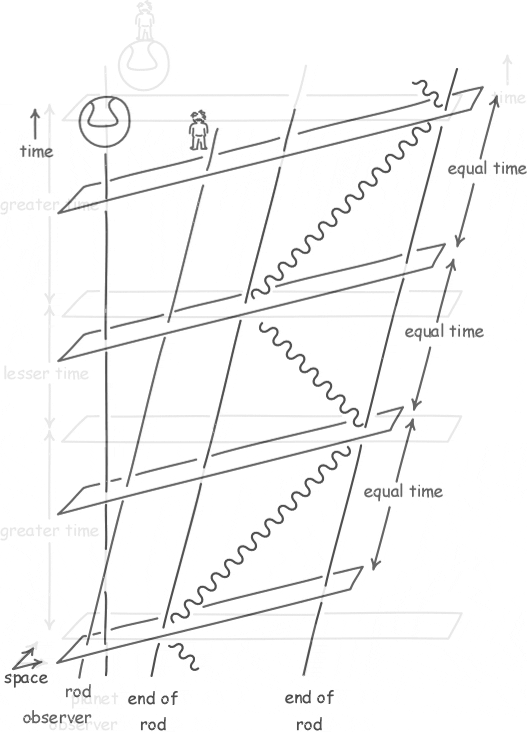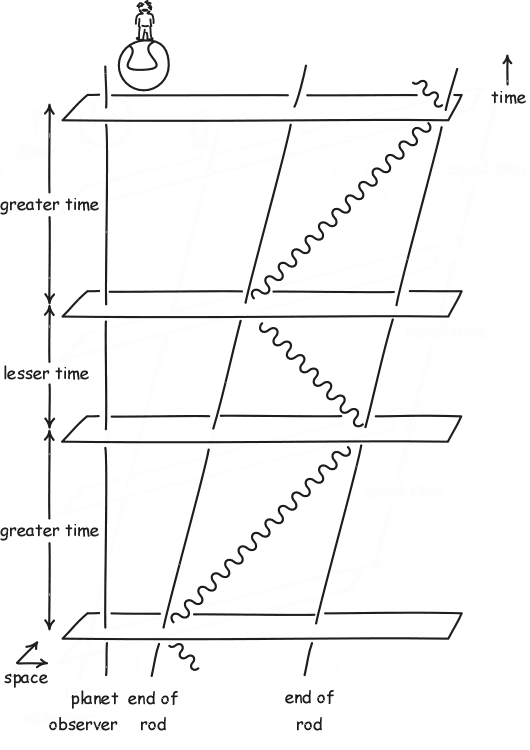 |
In comparing the last two
figures, the key element to notice is that the rod and bouncing
light signal remain the same. All that changes is the way
that the two observers slice up the spacetime into hypersurfaces of
simultaneity. The planet observer's slicing leads to the judgment that the light's forward journey takes longer. The rod observer's slicing leads to the judgment that the light's forward and return journeys take the same time. The animation at left shows the two figures overlayed and that the rod and light signal world lines are the same in both. |
Copyright John D. Norton. January 2001, September 2002; July 2006; February 3, 2007; January 23, September 24, 2008; January 21, 2010; February 1, 2012; September 24, 2015. August 26, 2018. February 3, 2022. September 22, 2024.