MATH2071: LAB 3: Implicit ODE methods

Introduction	Exercise 1
Stiff Systems	Exercise 2
Direction Field Plots	Exercise 3
The Backward Euler Method	Exercise 4
Newton's method	Exercise 5
The Trapezoid Method	Exercise 6
Matlab ODE solvers	Exercise 7
Backwards difference methods (Extra)	Exercise 8
	Exercise 9
	Exercise 10
	Extra Credit

Introduction

The explicit methods that we discussed last time are well suited to handling a large class of ODE's. These methods perform poorly, however, for a class of ``stiff'' problems that occur all too frequently in applications. We will examine implicit methods that are suitable for such problems. We will find that the implementation of an implicit method has a complication we didn't see with the explicit method: a (possibly nonlinear) equation needs to be solved.

The term ``stiff'' as applied to ODE's does not have a precise definition. Loosely, it means that there is a very wide range between the most rapid and least rapid (with ) changes in solution components. A reasonably good rule of thumb is that if Runge-Kutta or Adams-Bashforth or other similar methods require much smaller steps than you would expect, based on your expectations for the solution accuracy, then the system is probably stiff. The term itself arose in the context of solution for the motion of a stiff spring when it is being driven at a modest frequency of oscillation. The natural modes of the spring have relatively high frequencies, and the ODE solver must be accurate enough to resolve these high frequencies, despite the low driving frequency.

Stiff Systems

I've warned you that there are problems that defeat the explicit Runge-Kutta and Adams-Bashforth methods. In fact, for such problems, the higher order methods perform even more poorly than the low order methods. These problems are called ``stiff'' ODE's. We will only look at some very simple examples.

Consider the differential system

$\displaystyle y'$	$\displaystyle =\lambda(-y+\sin x)$
$\displaystyle y(0)$	$\displaystyle =0$	(1)

whose solution is

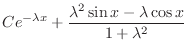$\displaystyle y(x)$	$\displaystyle =$	$\displaystyle Ce^{ - \lambda x }+ \frac{\lambda^{2}\sin x-\lambda\cos x}{1+\lambda^{2}}$
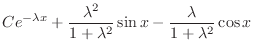	$\displaystyle =$	$\displaystyle Ce^{-\lambda x}+\frac{\lambda^2}{1+\lambda^2}\sin x -\frac{\lambda }{1+\lambda^2}\cos x$

for

a constant. For the initial condition

, the constant

can easily be seen to be

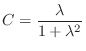
$\displaystyle C=\frac{\lambda }{1+\lambda^2}$

The ODE becomes stiff when ${\lambda}$ gets large: at least ${\lambda}=10$ , but in practice the equivalent of ${\lambda}$ might be a million or more. One key to understanding stiffness of this system is to make the following observations.

For large ${\lambda}$ and except very near , the solution behaves as if it were approximately $y(x)=\sin x$ , which has a derivative of modest size.
Small deviations from the curve $y(x)=\sin x$ (because of initial conditions or numerical errors) cause the solution to have large derivatives that depend on $\lambda$ .

In other words, the interesting solution has modest derivative and should be easy to approximate, but nearby solutions have large (depending on $\lambda$ ) derivatives and are hard to approximate. Again, this is characteristic of stiff systems of ODEs.

We will be using this stiff differential equation in the exercises below, and in the next section you will see a graphical display of stiffness for this equation.

Direction Field Plots

One way of looking at a differential equation is to plot its ``direction field.'' At any point , we can plot a little arrow $\bf p$ equal to the slope of the solution at . This is effectively the direction that the differential equation is ``telling us to go,'' sort of the ``wind direction.'' How can you find $\bf p$ ? If the differential equation is $y'=f_{\text{ode}}(x,y)$ , and $\bf p$ represents , then ${\bf p}=(dx,dy)$ , or ${\bf p}=h(1,f_{\text{ode}}(x,y))$ for a sensibly-chosen value . Matlab has some built-in functions to generate this kind of plot.

Exercise 1: In this exercise, you will see a graphical illustration of why a differential equation is ``stiff.''

Copy the following lines into a file called stiff4_ode.m:

function fValue = stiff4_ode ( x, y )
% fValue = stiff4_ode ( x, y ) 
% computes the right side of the ODE
%   dy/dx=f_ode(x,y)=lambda*(-y+sin(x)) for lambda = 4
% x is independent variable
% y is dependent variable
% output, fValue is the value of f_ode(x,y).

LAMBDA=4;
fValue = LAMBDA * ( -y + sin(x) );

Also copy the following lines into a second file called stiff4_solution.m.

function y = stiff4_solution ( x )
% y = stiff4_solution ( x )
% computes the solution of the ODE
%   dy/dx=f_ode(x,y)=lambda*(-y+sin(x)) for lambda = 4
% and initial condition y=0 at x=0
% x is the independent variable
% y is the solution value

LAMBDA=4;
y = (LAMBDA^2/(1+LAMBDA^2))*sin(x) + ...
    (LAMBDA  /(1+LAMBDA^2))*(exp(-LAMBDA*x)-cos(x));

Create new versions of these files, two using LAMBDA=55 and named stiff55_ode.m and stiff55_solution.m, and two using LAMBDA=10000 and named stiff10000_ode.m and stiff10000_solution.m.
The solution to our stiff ODE is roughly , so we are interested in values of between 0 and , and values of between -1 and 1. The Matlab meshgrid command is designed for that (it is kind of a two-dimensional linspace). To evaluate the direction vector , will be all 1's (use the Matlab ones function), and comes from our right hand side function. Finally, we use the Matlab command quiver to display the vector plot. Use the following commands to plot the direction field for the range of (x,y) values:
```
  h = 0.1;  % mesh size
  scale = 2.0; % make vectors longer
  [x,y] = meshgrid ( 0:h:2*pi, -1:h:1 );
  px = ones ( size ( x ) );
  py = stiff4_ode ( x, y );
  quiver ( x, y, px, py, scale ) 
  axis equal  %this command makes equal x and y scaling
```
Finally, to see how the direction field relates to the approximate solution, plot the function on the same frame.
```
  hold on
  x1=(0:h:2*pi);
  y1=stiff4_solution(x1);
  plot(x1,y1,'r')  % solution will come out red.
  hold off
```
Send me a copy of your plot (print -djpeg ex1.jpg, or File Export and choose jpeg).

Look at your direction field full-screen. You can see the solution in red and all the arrows point toward it. Basically, no matter where you start in the rectangle, you head very rapidly (long arrows) toward $\sin x$ , and then follow that curve as it varies slowly (short arrows). Some numerical methods overshoot the solution curve in their enthusiasm to reach it, as you will see in the following exercise, and avoiding this overshoot characterizes methods for stiff systems.

Exercise 2: In this exercise, you will be seeing a numerical illustration of why an ODE is ``stiff.''

Using LAMBDA=10000 to represent a stiff equation, how many points would be needed in the interval [0,2*pi] to make a pleasing plot of stiff10000_solution(x)?
```
x=linspace(0,2*pi,10);  % try 10, 20, 40, etc.
plot(x,stiff10000_solution(x))
```
Try it, but I think you will agree with me that it takes about 40 evenly-spaced points to make a reasonable curve. Do not send me copies of your plots.
Now, choose either of forward_euler.m, or rk3.m from last lab and attempt to solve stiff10000_ode.m over the interval [0,2*pi], starting from the initial condition y=0 at x=0 and using 40 steps. Your solutions blow up (are unstable), don't they? (If you are plotting the solutions, look at the scale!) Multiply the number of steps by 10 repeatedly until you get something reasonable, i.e., try 40, 400, 4000, etc. steps. How many steps does it take to get a reasonable plot? It takes many more steps to get a reasonable solution than you would expect, based on solution accuracy, and this behavior is characteristic of stiff systems.

The Backward Euler Method

The Backward Euler method is an important variation of Euler's method. Before we say anything more about it, let's take a hard look at the algorithm:

$\displaystyle x_{k+1}$	$\displaystyle =$	$\displaystyle x_k+h$
$\displaystyle y_{k+1}$	$\displaystyle =$	$\displaystyle y_{k} + h f_{\text{ode}}(x_{k+1},y_{k+1})$	(2)

You might think there is no difference between this method and Euler's method. But look carefully-this is not a ``recipe,'' the way some formulas are. Since $y_{k+1}$ appears both on the left side and the right side, it is an equation that must be solved for $y_{k+1}$ , i.e., the equation defining $y_{k+1}$ is implicit. It turns out that implicit methods are much better suited to stiff ODE's than explicit methods.

If we plan to use Backward Euler to solve our stiff ode equation, we need to address the method of solution of the implicit equation that arises. Before addressing this issue in general, we can treat the special case:

$\displaystyle x_{k+1}$	$\displaystyle =$	$\displaystyle x_k+h$
$\displaystyle y_{k+1}$	$\displaystyle =$	$\displaystyle y_{k} + h \lambda (-y_{k+1} + \sin x_{k+1} )$	(3)

This equation can be solved for $y_{k+1}$ easily enough! The solution is

$\displaystyle x_{k+1}$	$\displaystyle =$	$\displaystyle x_k+h$
$\displaystyle y_{k+1}$	$\displaystyle =$	$\displaystyle (y_{k} + h \lambda \sin x_{k+1} )/(1 + h \lambda)$

In the following exercise, we will write a version of the backward Euler method that implements this solution, and only this solution. Later, we will look at more general cases.

Exercise 3:

Write a function m-file called back_euler_lam.m with signature line
```
function [x,y]=back_euler_lam(lambda,xRange,yInitial,numSteps)
% [x,y]=back_euler_lam(lambda,xRange,yInitial,numSteps)
% comments

% your name and the date.
```
that implements the above algorithm You may find it helpful to start out from a copy of your forward_euler.m file, but if you do, be sure to realize that this function has lambda as its first input parameter instead of the function name f_ode that forward_euler.m has. This is because back_euler_lam solves only the particular linear equation (3).
Be sure to include comments following the signature line.
Test back_euler_lam by solving the system (1) with $\lambda=10000$ over the interval $[0,2\pi]$ , starting from the initial condition at x=0 for 40 steps. Your solution should not blow up and its plot should look reasonable. Please include this plot with your summary.
Plot the solution you just generate using back_euler_lam using 40 steps and the solution you generated in Exercise 2 using either forward_euler or rk3 with a large number of steps on the same plot (use hold on). These solutions should be very close. Please include this plot with your summary.
For the purpose of checking your work, the first few values of y are y=[ 0.0; 0.156334939127; 0.308919855800; 0.453898203657; ...]. Did you get these values?

In the next exercise, we will compare backward Euler with forward Euler for accuracy. Of course, backward Euler gives results when the stepsize is large and Euler does not, but we are curious about the case that there are enough steps to get answers. Because it would require too many steps to run this test with $\lambda=$ 1.e4, you will be using $\lambda=$ 55.

Exercise 4:

Fill in the table below, using the value lambda=55. Compute the error in the solution versus the exact solution as

  abs( y(end) - stiff55_solution(x(end)) )

Compute the ratios of the errors for each value of numSteps divided by the error for the succeeding value of numSteps. Use back_euler_lam to fill in the following table, over the interval [0,2*pi] and starting from yInit=0.

             lambda=55
numSteps back_euler_lam error   ratio
   40    ____________________  __________
   80    ____________________  __________
  160    ____________________  __________
  320    ____________________  __________
  640    ____________________  __________
 1280    ____________________  __________
 2560    ____________________

Based on the ratios in the table, estimate the order of accuracy of the method, i.e., estimate the exponent in the error estimate . is an integer in this case.

Repeat this experiment using forward_euler, and fill in the following table. Note that the errors using euler end up being about the same size as those using back_euler_lam, once euler starts to behave.

           lambda=55 Error comparison
numSteps  back_euler_lam        forward_euler      
   40    ___________________   _________________
   80    ___________________   _________________
  160    ___________________   _________________
  320    ___________________   _________________
  640    ___________________   _________________
 1280    ___________________   _________________
 2560    ___________________   _________________

(In filling out this table, please include at least four significant figures in your numbers. You can use format long or format short e to get the desired precision.)

Compare the order of accuracy using forward_euler with that using back_euler_lam.

Newton's method

You should be convinced that implicit methods are worth while. How, then, can the resulting implicit equation (usually it is nonlinear) be solved? The Newton (or Newton-Raphson) method is a good choice. (We saw Newton's method last semester in Math 2070, Lab 4, you can also find discussions of Newton's method by Quarteroni, Sacco and Saleri in Chapter 7.1 or in a Wikipedia article http://en.wikipedia.org/wiki/Newton's_method.) Briefly, Newton's method is a way to solve equations by successive iterations. It requires a reasonably good starting point and it requires that the equation to be solved be differentiable. Newton's method can fail, however, and care must be taken so that you do not attempt to use the result of a failed iteration. When Newton's method does fail, it is mostly because the provided Jacobian matrix is not, in fact, the correct Jacobian for the provided function.

Suppose you want to solve the nonlinear (vector) equation

$\displaystyle {\bf F(Y)}={\bf0}$

(4)

and you know a good starting place ${\bf Y}_{0}$ . The following iteration is called Newton iteration.

$\displaystyle {\bf Y}^{(n+1)}-{\bf Y}^{(n)}=\Delta {\bf Y}^{(n)}= -({\bf J}^{(n)})^{-1} ({\bf F}({\bf Y}^{(n)}))$

(5)

where $\mathbf{J^{(n)}}$ denotes the partial derivative of $\mathbf{F}$ evaluated at $\mathbf{Y}^{(n)}$ . If $\mathbf{F}$ is a scalar function of a scalar variable, $\mathbf{J}=\partial \mathbf{F} /\partial\mathbf{Y}$ . In the case that ${\bf Y}$ is a vector, the partial derivative must be interpeted as the Jacobian matrix, with components defined as

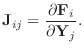
$\displaystyle \mathbf{J}_{ij}=\frac{\partial \mathbf{F}_i}{\partial \mathbf{Y}_j}.$

The superscript

is used here to distinguish the iteration number n from the step number, k. Newton's method (usually) converges quite rapidly, so that only a few iterations are required.

There is an easy way to remember the formula for Newton's method. Write the finite difference formula for the derivative as

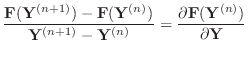
$\displaystyle \frac{\mathbf{F}(\mathbf{Y}^{(n+1)})-\mathbf{F}(\mathbf{Y}^{(n)})... ...hbf{Y}^{(n)}} =\frac{\partial\mathbf{F}(\mathbf{Y}^{(n)})}{\partial\mathbf{Y}}$

or, for vectors and matrices,

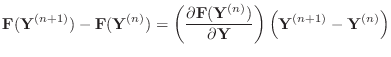
$\displaystyle {\mathbf{F}(\mathbf{Y}^{(n+1)})-\mathbf{F}(\mathbf{Y}^{(n)})} =\l... ...rtial\mathbf{Y}}\right) \left({ \mathbf{Y}^{(n+1)} - \mathbf{Y}^{(n)}}\right)$

and then take $\mathbf{F}(\mathbf{Y}^{(n+1)})=0$ , because that is what you are wishing for, and solve for $\mathbf{Y}^{(n+1)}$ .

On each step, the backward Euler method requires a solution of the equation

$\displaystyle y_{k+1}=y_k+hf_{\text{ode}}(x_{k+1},y_{k+1})$

so that we can take $y_{k+1}$ to be the solution, $\bf Y$ , of the system ${\bf F(Y)}={\bf0}$ , where

$\displaystyle {\bf F(Y)}=y_k+hf_{\text{ode}}(x_{k+1},{\bf Y})-{\bf Y}.$

(6)

When we have found a satisfactorily approximate solution ${\bf Y}^{(n)}$ to (6), then we take $y_{k+1}={\bf Y}^{(n)}$ and proceed with the backward Euler method. We think of each of the values ${\bf Y}^{(n)}$ as successive corrections to $y_{k+1}$ .

I call your attention to a difficulty that has arisen. For the Euler, Adams-Bashforth and Runge-Kutta methods, we only needed a function that computed the right side of the differential equation. In order to carry out the Newton iteration, however, we will also a function that computes the partial derivative of the right side with respect to . In 2070 we assumed that the derivative of the function was returned as a second variable, and we will use the same convention here.

To summarize, on each time step, start off the iteration by predicting the solution using an explict method. Forward Euler is appropriate in this case. Then use Newton's method to generate successive correction steps. In the following exercise, you will be implementing this method.

Exercise 5:

Change your stiff10000_ode.m so that it has the signature
```
function [fValue, fPartial]=stiff10000_ode(x,y)
% [fValue, fPartial]=stiff10000_ode(x,y)
% comments

% your name and the date
```
and computes the partial derivative of stiff10000_ode with respect to y, fPartial. To do this, write the derivative of the formula for stiff10000_ode out by hand, then program it. attempt to use symbolic differentiation inside the function stiff1000_ode. Do not attempt to use symbolic differentiation inside the function stiff1000_ode.
Similarly, change the signature for stiff55_ode. There is no need to change stiff1_ode because you won't be using it again.

Copy the following function to a file named back_euler.m using cut-and-paste.

function [x,y]=back_euler(f_ode,xRange,yInitial,numSteps)
% [x,y]=back_euler(f_ode,xRange,yInitial,numSteps) computes
% the solution to an ODE by the backward Euler method
%
% xRange is a two dimensional vector of beginning and
%   final values for x
% yInitial is a column vector for the initial value of y
% numSteps is the number of evenly-spaced steps to divide
%   up the interval xRange
% x is a row vector of selected values for the 
%   independent variable
% y is a matrix. The k-th column of y is 
%   the approximate solution at x(k)

% your name and the date

% force x to be a row vector
x(1,1) = xRange(1);
h = ( xRange(2) - xRange(1) ) / numSteps;
y(:,1) = yInitial;
for k = 1 : numSteps
  x(1,k+1) = x(1,k) + h;

  Y = (y(:,k)) + h * f_ode( x(1,k), y(:,k));
  [Y,isConverged]= newton4euler(f_ode,x(k+1),y(:,k),Y,h);

  if ~ isConverged
    error(['back_euler failed to converge at step ', ...
          num2str(k)])
  end

  y(:,k+1) = Y;
end

Copy the following function to a file named newton4euler.m (Read this name as ``Newton for Euler.'')

function [Y,isConverged]=newton4euler(f_ode,xkp1,yk,Y,h)
% [Y,isConverged]=newton4euler(f_ode,xkp1,yk,Y,h)
% special function to evaluate Newton's method for back_euler

% your name and the date

TOL = 1.e-6;
MAXITS = 500;
 
isConverged= (1==0);  % starts out FALSE
for n=1:MAXITS
  [fValue fPartial] = f_ode( xkp1, Y);
  F = yk + h * fValue - Y;
  J = h * fPartial - eye(numel(Y));
  increment=J\F;
  Y = Y - increment;
  if norm(increment,inf) < TOL*norm(Y,inf)
    isConverged= (1==1);  % turns TRUE here
    return
  end
end

Insert the following comments into either back_euler.m or newton4euler.m (or both) where they belong. Some comments belong in both files. Include copies of both files when you send your summary to me.

% f_ode is the handle of a function whose signature is ???
% TOL = ??? (explain in words what TOL is used for)
% MAXITS = ??? (explain in words what MAXITS is used for)
% When F is a column vector and J a matrix, 
  % the expression J\F means ???
% The Matlab function "eye" is used for ???
% The following for loop performs the spatial stepping (on x)
% The following statement computes the initial guess for Newton

If the function $\mathbf{F}(\mathbf{Y})$ is given by , and , and if and , write out the values of $\mathbf{J}(\mathbf{Y})=\partial\mathbf{F}/\partial\mathbf{Y}$ and $\mathbf{F}(\mathbf{Y})$ as a Matlab matrix and vector, respectively. Be careful to distinguish row and column vectors.
The equation (5) includes the quantities $\mathbf{J}^{(n)}$ , $\Delta {\bf Y}$ , and ${\bf F}({\bf Y}^{(n)})$ . What are the names of the variables in the code representing these mathematical quantities?
Insert a comment in the code indicating which lines implement Equation (5).
Insert a comment in the code indicating which lines implement Equation (6). (Note: This line is specific to the implicit Euler method, and will have to be changed when the method is changed.)
In the case that numel(Y)>1, is Y a row vector or a column vector?
If f_ode=@stiff10000_ode, xkp1=2.0, yk=1.0, h=0.1, and the initial guess Y=1, write out by hand the (linear) equation that newton4euler solves. To do this, start from (6), with $\mathbf{F}(\mathbf{Y})=0$ . Plug in the formula for $f_{\text{ode}}$ and solve for $\mathbf{Y}$ in terms of everything else. What is the value of the solution, $\mathbf{Y}$ , of this linear equation? Please include at least eight significant digits for the result.
Verify that newton4euler is correct by showing it yields the same value you just computed by hand for the case that f_ode=@stiff10000_ode, xkp1=2.0, yk=1.0, h=0.1, and the initial guess Y=1. (If you discover that the Newton iteration fails to converge, you probably have the derivative in stiff10000_ode wrong.)
In order to check that everything is programmed correctly, solve the ODE using stiff10000_ode, on the interval $[0,2\pi]$ , with initial value 0, for 40 steps, just as in Exercise 3, but use back_euler. Compare your solution with the one using lambda=10000 in back_euler_lam.m. You can compare all 40 values at once by taking the norm of the difference between the two solutions generated by back_euler_lam and back_euler. The two solutions should agree to ten or more significant digits. (Testing code by comparison with previous code is called ``regression'' testing.)

One simple nonlinear equation with quite complicated behavior is van der Pol's equation. This equation is written

$\displaystyle z'' + a(z^2-1) z' + z = e^{-x}$

where $e^{-x}$ has been chosen as a forcing term that dies out as

gets large. When

, this equation behaves somewhat as an oscillator with negative feedback (``damped'' or ``stable''), but when

is small then it looks like an oscillator with positive feedback (``negatively damped'' or ``positive feedback'' or ``unstable''). When

is small, it grows. When

is large, it dies off. The result is a non-linear oscillator. Physical systems that behave somewhat as a van der Pol oscillator include electrical circuits with semiconductor devices such as tunnel diodes in them (see this web page http://www.math.duke.edu/education/ccp/materials/diffeq/vander/vand1.html) and some biological systems, such as the beating of a heart, or the firing of neurons. In fact, van der Pol's original paper was, ``The Heartbeat considered as a Relaxation oscillation, and an Electrical Model of the Heart,'' Balth. van der Pol and J van der Mark, Phil. Mag. Suppl. 6(1928) pp 763--775. More information is available in an interesting Scholarpedia article http://www.scholarpedia.org/article/Van_der_Pol_oscillator.

As you know, van der Pol's equation can be written as a system of first-order ODEs in the following way.

$\displaystyle y'_1$	$\displaystyle =$	$\displaystyle f_1(x,y_1,y_2)=y_2$
$\displaystyle y'_2$	$\displaystyle =$	$\displaystyle f_2(x,y_1,y_2)=-a(y_1^2-1)y_2-y_1+e^{-x}$	(7)

where

and

The matrix generalization of the partial derivative in Newton's method is the Jacobian matrix:

$\displaystyle J=\left[\begin{array}{cc} \frac{\partial f_1}{\partial y_1} & \fr... ...rtial f_2}{\partial y_1} & \frac{\partial f_2}{\partial y_2} \end{array}\right]$

(8)

Exercise 6: In this exercise you will be solving van der Pol's equation with

using back_euler.

Write an m-file to compute the right side of the van der Pol system (7) and its Jacobian (8). The m-file should be named vanderpol_ode.m and should have the signature

function [fValue, J]=vanderpol_ode(x,y)
% [fValue, J]=vanderpol_ode(x,y)
% more comments
% your name and the date

if numel(y) ~=2
  error('vanderpol_ode: y must be a vector of length 2!')
end

a=11;

fValue = ???

df1dy1 = 0;
df1dy2 = ???
df2dy1 = ???
df2dy2 = -a*(y(1)^2-1);

J=[df1dy1 df1dy2
   df2dy1 df2dy2];

be sure that fValue is a column and that the value of the parameter

Solve the van der Pol system twice, once using forward_euler and once using back_euler. Solve over the interval from x=0 to x=2, starting from y=[0;0] and using 40 intervals. You can see by plotting the solutions that forward_euler does not give a good solution (it has some up/down oscillations) while back_euler does. Send me plots of both solutions with your summary. (Note: If you get a message saying that convergence failed, you probably have an error in your calculation of the derivatives in J. Fix it.)
Solve the system again, this time using 640 intervals. This time both methods should remain stable and the answers should be close. Please include plots of both solutions on a single frame with your summary. (Use hold on and hold off.)

The Trapezoid Method

You have looked at the forward Euler and backward Euler methods. These methods are simple and involve only function or Jacobian values at the beginning and end of a step. They are both first order, though. It turns out that the trapezoid method also involves only values at the beginning and end of a step and is second order accurate, a substantial improvement. This method is also called ``Crank-Nicolson,'' especially when it is used in the context of partial differential equations. As you will see, this method is appropriate only for mildly stiff systems.

The trapezoid method can be derived from the trapezoid rule for integration. It has a simple form:

$\displaystyle x_{k+1}$	$\displaystyle =$	$\displaystyle x_k+h$
$\displaystyle y_{k+1}$	$\displaystyle =$	$\displaystyle y_{k} + \frac{h}2 ( f_{\text{ode}}(x_{k},y_{k}) + f_{\text{ode}}(x_{k+1},y_{k+1}))$	(9)

from which you can see that this is also an ``implicit'' formula. The backward Euler and Trapezoid methods are the first two members of the ``Adams-Moulton'' family of ODE solvers.

In the exercise below, you will write a version of the trapezoid method using Newton's method to solve the per-timestep equation, just as with back_euler. As you will see in later exercises, the trapezoid method is not so appropriate when the equation gets very stiff, and Newton's method is overkill when the system is not stiff. The method can be successfully implemented using an approximate Jacobian or by computing the Jacobian only occasionally, resulting in greater computational efficiency. We are not going to pursue these alternatives in this lab, however.

Exercise 7:

Make a copy of your back_euler.m file, naming the copy trapezoid.m. Modify it to have the signature:
```
function [ x, y ] = trapezoid ( f_ode, xRange, yInitial, numSteps )
% comments
```
Add appropriate comments below the signature line.

Replace the line

  [Y,isConverged]= newton4euler(f_ode,x(k+1),y(:,k),Y,h);

with the new line

  [Y,isConverged]=newton4trapezoid(f_ode,x(1,k),x(1,k+1),y(:,k),Y,h);

Make a copy of your newton4euler.m, naming the copy newton4trapezoid.m.

Change the signature of newton4trapezoid to

function [Y,isConverged]=newton4trapezoid(f_ode,xk,xkp1,yk,Y,h)

In order to implement the trapezoid method, you need to write the function that appears in (5) and (6) so it is valid for the trapezoid rule. In the code you copied from mewtpm4ei;er, it is written for the backward Euler method (6) and must be changed for use in the trapezoid method. To do this, consider (9), repeated here

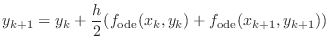
$\displaystyle y_{k+1}=y_{k} + \frac{h}2 ( f_{\text{ode}}(x_{k},y_{k}) + f_{\text{ode}}(x_{k+1},y_{k+1}))$

and replace $y_{k+1}$ with and bring everything to the right. Then write

$\displaystyle F(Y)=0=$ right side $\displaystyle .$

Modify newton4trapezoid.m to solve this function. Do not forget to modify the Jacobian J $J_{ij}=\frac{\partial F_i}{\partial Y_j}$ to reflect the new function F. Remember, if you have the Jacobian wrong, the Newton iteration may fail.
Test your newton4trapezoid code for the case f_ode=@stiff55_ode, xk=1.9, xkp1=2.0, yk=1.0, h=0.1, and the initial guess for Y=1.
Write out by hand the (linear) equation that newton4trapezoid solves in the case f_ode=@stiff55_ode, xk=1.9, xkp1=2.0, yk=1.0, and h=0.1. Be sure your solution to this equation agrees with the one from newton4trapezoid to at least 10 decimal places. If not, find the mistake and fix it.

Test the accuracy of the trapezoid method by computing the numerical solution of stiff55_ode.m (starting from

over the interval $x\in[0,2\pi]$ , and fill in the following table. Compute ``error'' as the difference between the computed and exact values at $x=2\pi$ .

             stiff55
numSteps  trapezoid error         ratio
  10     ____________________  __________
  20     ____________________  __________
  40     ____________________  __________
  80     ____________________  __________
 160     ____________________  __________
 320     ____________________

Are your results consistent with the theoretical convergence rate of the trapezoid rule? If not, you have a bug you need to fix.

In the following exercise, you are going to see that the difference in accuracy between the trapezoid method and the backward Euler method for solution of the vander Pol equation.

Exercise 8:

Use trapezoid.m to solve the van der Pol equation (a=11) on the interval [0,10] starting from the column vector [0,0] using 100, 200, 400, and 800 steps, and plot both components of all four solutions on one plot. You should see that the solution for 400 steps is pretty much the same as the one for 800 steps, and the others are different, especially in the second component (derivative). We will assume that the final two approximate solutions represent the correct solution. Please send me this plot with your summary. Hint: you can generate this plot easily with the following sequence of commands.
```
hold off
[x,y]=trapezoid(@vanderpol_ode,[0,10],[0;0],100);plot(x,y)
hold on
[x,y]=trapezoid(@vanderpol_ode,[0,10],[0;0],200);plot(x,y)
[x,y]=trapezoid(@vanderpol_ode,[0,10],[0;0],400);plot(x,y)
[x,y]=trapezoid(@vanderpol_ode,[0,10],[0;0],800);plot(x,y)
hold off
```
Use back_euler.m to solve the van der Pol equation on the interval [0,10] starting from the value [0;0] using 400, 800, 3200, and 12800 steps, and plot all four solutions on one plot. The larger number of points may take a minute. You should see a progression of increasing accuracy in the second ``pulse.'' Please send me this plot with your summary.
Plot the 12800-step back_euler solution and the 800-step trapezoid solution on the same plot. You should see they are close. Please send me this plot with your summary.

The trapezoid method is unconditionally stable, but this fact does not mean that it is good for very stiff systems. In the following exercise, you will apply the trapezoid method to a very stiff system so you will see that numerical errors arising from the initial rapid transient persist when using the trapezoid rule but not for backwards Euler.

Exercise 9:

Solve the stiff10000_ode system twice on the interval [0,10] starting from yInitial=0.1 using 100 steps. Note that the initial condition is not zero. Use both the trapezoid method and backwards Euler, and plot both solutions on the same plot. Send me this plot with your summary file.
Use the trapezoid method to solve the same case using 200, 400, 800, and 1600 steps. Plot each solution on its own plot. You should see that the effect of the initial condition is not easily eliminated. Please include the 1600 step case when you send your summary file.

Matlab ODE solvers

Matlab has a number of built-in ODE solvers. These include:

Matlab ODE solvers
ode23	non-stiff, low order
ode113	non-stiff, variable order
ode15s	stiff, variable order, includes DAE
ode23s	stiff, low order
ode23t	trapezoid rule
ode23tb	stiff, low order
ode45	non-stiff, medium order (Runge-Kutta)

All of these functions use the very best methods, are highly reliable, use adaptive step size control, and allow close control of errors and other parameters. As a bonus, they can be ``told'' to precisely locate interesting events such as zero crossings and will even allow user-written functions to be called when certain types of events occur. There is very little reason to write your own ODE solvers unless you are actively researching new methods. In the following exercise you will see how to use these solvers in a very simple case.

The ODE solvers we have written have four parameters, the function name, the solution interval, the initial value, and the number of steps. The Matlab solvers use a good adaptive stepping algorithm, so there is no need for the fourth parameter.

The Matlab ODE solvers require that functions such as vanderpol_ode.m return column vectors and there is no need for the Jacobian matrix. Thus, the same vanderpol_ode.m that you used for back_euler will work for the Matlab solvers. However, the format of the matrix output from the Matlab ODE solvers is the transpose of the one from our solvers! Thus, while y(:,k) is the (column vector) result achieved by back_euler on step k, the result from the Matlab ODE solvers will be y(k,:)!

Exercise 10: For this exercise, Set a=55 in vanderpol_ode.m to exhibit some stiffness.

You can watch a solution evolve if you call the solver without any output variables. Use ode45 to solve the van der Pol problem with a=55 and solve on the interval [0,70] starting from [0;0]. Use the following Matlab command:
```
ode45(@vanderpol_ode,[0,70],[0;0])
```
Please include this plot with your summary.
You can see the difference between a stiff solver and a non-stiff solver on a stiff equation such as stiff10000_ode by comparing ode45 with ode15s. (These are my personal favorites.) You can see both plots with the commands
```
figure(2)
ode45(@stiff10000,[0,8],1);
title('ode45')
figure(3)
ode15s(@stiff10000,[0,8],1);
title('ode15s')
```
You should be able to see that the step density (represented by the little circles on the curves) is less for ode15s. This density difference is most apparent in the smooth portions of the curve where the solution derivative is small. You do not need to send me these plots.
If you wish to examine the solution of vanderpol_ode in more detail, or manipulate it, you need the solution values, not a picture. You can get the solution values with commands similar to the following:
```
[x,y]=ode15s(@vanderpol_ode,[0,70],[0;0]);
```
If you wish, you can plot the solution, compute its error, etc. For this solution, what is the value of at x=70 (please give at least six significant digits)? How many steps did it take? (The length of x is one more than the number of steps.)
Suppose you want a very accurate solution. The default tolerance is .001 relative accuracy in Matlab, but suppose you want a relative accuracy of 1.e-8? There is an extra variable to provide options to the solver. It works in the following manner:
```
myoptions=odeset('RelTol',1.e-8);
[x,y]=ode15s(@vanderpol_ode,[0,70],[0;0],myoptions);
```
Use help odeset for more detail about options, and use the command odeset alone to see the default options. How many steps did it take this time? What is the value of at x=70 (to at least six significant digits)?

Remark: The functionality of the Matlab ODE solvers is available in external libraries that can be used in Fortran, C, C++ or Java programs. One of the best is the Sundials package from Lawrence Livermore https://computation.llnl.gov/casc/sundials/main.html or odepack from Netlib http://www.netlib.org/odepack/.

Extra credit: Backwards difference methods (8 points)

You saw the Adams-Bashforth (explicit) methods in the previous lab. The second-order Adams-Bashforth method (ab2) achieves higher order without using intermediate points (as the Runge-Kutta methods do), but instead uses points earlier in the evolution history, using the points and $y_{k-1}$ , for example, for ab2. Among implicit methods, the ``backwards difference methods'' also achieve higher order accuracy by using points earlier in the evolution history. It turns out that backward difference methods are good choices for stiff problems.

The backward difference method of second order can be written as

$\displaystyle y_{k+1}=\frac43y_k-\frac13 y_{k-1}+\frac23h f_{\text{ode}}(x_{k+1},y_{k+1}).$

(10)

It is an easy exercise using Taylor series to show that the truncation error is

per step, or

over the interval

Exercise 11: In this exercise, you will write a function m-file named bdm2.m to implement the second order backward difference method (10).

Write a function m-file with the signature
```
function [ x, y ] = bdm2 ( f_ode, xRange, yInitial, numSteps )
% [ x, y ] = bdm2 ( f_ode, xRange, yInitial, numSteps )
% ... more comments ...

% your name and the date
```
Although it would be best to start off the time stepping with a second-order method, for simplicity you should take one backward Euler step to start off the stepping. You should model the function on back_euler.m, and, with some ingenuity, you can use newton4euler without change. (If you cannot see how, just write a new Newton solver routine.)
Test your function by solving the system (1) for $\lambda=55$ over the interval $[0,2\pi]$ starting at 0. Check the function for 40, 80, 160, and 320 intervals, and show that convergence is .
Using , solve vanderpol_ode over the interval starting from using 200 points, plot and compare it with the one from trapezoid. They should be close.
Using , solve vanderpol_ode over the interval starting from using 200 points, plot and compare it with the one from trapezoid. You should observe that bdm2 does not exhibit the plus/minus oscillations that can be seen in the trapezoid solution, especially in the second component (the derivative).

Back to MATH2071 page.

kimwong 2019-01-31