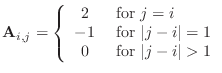
In many numerical applications, notably the ordinary and partial differential equations this semester, the single most time-consuming step is the solution of a system of linear equations. We now begin a major topic in Numerical Analysis, Numerical Linear Algebra. We assume you are familiar with the concepts of vectors and matrices, matrix multiplication, vector dot products, and the theory of the solution of systems of linear equations, the matrix inverse, eigenvalues and so on. We now concentrate on the practical aspects of carrying out the computations required to do linear algebra in a numerical setting.
This lab will take three sessions.
We begin by noting several special test matrices that we will refer to when trying out algorithms. Then we state the linear system problem and consider three methods of solution, using the determinant, the inverse matrix, or Gauß factorization. We will find that factorization into three simply-solved factors is the best way to go, and we will write a m-file to perform the factorization and another to solve systems given the factorization. We will end up with an example using our m-files as part of the numerical solution of a partial differential equation.
We will now consider a few simple test matrices that we can use to study the behavior of the algorithms for solution of a linear system. We can use such problems as a quick test that we haven't made a serious programming error, but more importantly, we also use them to study the accuracy of the algorithms. We want test problems which can be made any size, and for which the exact values of the determinant, inverse, or eigenvalues can be determined. Matlab itself offers a ``rogues' gallery'' of special test matrices through the Matlab function gallery, and it offers several special matrices. We will use our own functions for some matrices and Matlab's functions for others.
Some test matrices we will be using are:
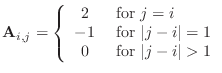
So that the matrix looks like:
![$\displaystyle \left( \begin{array}{rrrrrr}
2 & -1 & & & & \\
-1 & 2 & -1 & &...
...ddots & & [7pt]
& & & -1 & 2 & -1 \\
& & & &-1 & 2
\end{array} \right)
$](img2.png)
where blanks represent zero values. As you have seen, the matrix is positive definite, symmetric, and tridiagonal. The determinant is
Do not use the gallery('tridiag',n) form in these labs except when instructed to use it. Matlab has two forms of storage for matrices, ``sparse'' and ``full.'' Everything we have done so far has used the ``full'' form, but gallery('tridiag',n) returns the ``sparse'' form. The ``sparse'' matrix form requires some special handling.
Download the m-file, dif2.m now.
Row ![]() of the
of the ![]() Frank matrix has the formula:
Frank matrix has the formula:
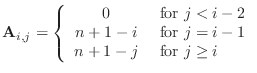
The Frank matrix for

The determinant of the Frank matrix is 1, but is difficult to compute accurately because of roundoff errors. This matrix has a special form called Hessenberg form wherein all elements below the first subdiagonal are zero. Matlab provides the Frank matrix in its ``gallery'' of matrices, gallery('frank',n), but we will use an m-file frank.m. It turns out that the inverse of the Frank matrix also has a simple formula.
Download the m-file frank.m now.
![$\displaystyle \left(\begin{array}{ccccc}
\frac11& \frac12& \frac13& \frac14& \f...
...\frac18 [5pt]
\frac15& \frac16& \frac17& \frac18& \frac19
\end{array}\right)
$](img12.png)
The Hilbert matrix arises in interpolation and approximation contexts
because it happens that
![]() . The
Hilbert matrix is at once nice because its inverse has integer elements
and also not nice because it is difficult to compute
the inverse accurately using the usual formulæ to invert a matrix.
. The
Hilbert matrix is at once nice because its inverse has integer elements
and also not nice because it is difficult to compute
the inverse accurately using the usual formulæ to invert a matrix.
Matlab has special functions for the Hilbert matrix and its inverse, called hilb(n) and invhilb(n), and we will be using these functions in this lab.
![$\displaystyle P=
\left(\begin{array}{ccccc}
\textcolor{blue}{1}&\textcolor{blue...
...0}& {35} [5pt]
\textcolor{blue}{1}& {5}& {15}& {35}& {70}
\end{array}\right)
$](img15.png)
As you can tell, the colored portion of this matrix is a Pascal triangle, written on its side.
A related lower triangular matrix can be written (for ![]() ) as
) as
![$\displaystyle L=
\left(\begin{array}{ccccc}
1& 0& 0& 0& 0 [5pt]
1& -1& 0& 0& ...
...-2& 1& 0& 0 [5pt]
1& -3& 3& -1& 0 [5pt]
1& -4& 6& -4& 1
\end{array}\right)
$](img16.png)
Except for signs, this matrix is a Pascal triangle written asymmetrically. The matrix
![$\displaystyle L_1=
\left(\begin{array}{ccccc}
1& 0& 0& 0& 0 [5pt]
1& 1& 0& 0&...
...]
1& 2& 1& 0& 0 [5pt]
1& 3& 3& 1& 0 [5pt]
1& 4& 6& 4& 1
\end{array}\right)
$](img17.png)
is truly a Pascal triangle written asymmetrically. Matlab provides a function pascal so that P=pascal(5), L=pascal(5,1), and L1=abs(L).
The Pascal matrix, like the Frank matrix, is very ill-conditioned for large values of ![]() . In addition,
the Pascal matrix satisfies the conditions
. In addition,
the Pascal matrix satisfies the conditions
More information is available in a Wikipedia article http://en.wikipedia.org/wiki/Pascal_matrix
The linear system ``problem'' can be posed in the following way. Find
an ![]() -vector
-vector ![]() that satisfies the matrix equation
that satisfies the matrix equation
You probably already know that there is ``usually" a solution if the
matrix is square, (that is, if ![]() ). We will concentrate on
this case for now. But you may wonder if there is an intelligent
response to this problem for the cases of a square but singular matrix,
or a rectangular system, whether overdetermined or underdetermined.
). We will concentrate on
this case for now. But you may wonder if there is an intelligent
response to this problem for the cases of a square but singular matrix,
or a rectangular system, whether overdetermined or underdetermined.
At one time or another, you have probably been introduced to several algorithms for producing a solution to the linear system problem, including Cramer's rule (using determinants), constructing the inverse matrix, Gauß-Jordan elimination and Gauß factorization. We will see that it is usually not a good idea to construct the inverse matrix and we will focus on Gauß factorization for solution of linear systems.
We will be concerned about several topics:
A classic result from linear algebra is the following:
Theorem The linear system problem (1) is uniquely
solvable for arbitrary ![]() if and only if
the inverse matrix
if and only if
the inverse matrix
![]() exists. In this
case the solution
exists. In this
case the solution ![]() can be expressed as
can be expressed as
![]() .
.
So what's the catch? There are a few:
In the following exercises, you will see that constructing the inverse
matrix takes time proportional to ![]() (for an
(for an ![]() matrix), as
does simply solving the system, but that solving the system is several
times faster than constructing the inverse matrix. You will also see
that matrices with special formats, such as tridiagonal matrices,
can be solved very efficiently. And you will see even simple
matrices can be difficult to numerically invert.
matrix), as
does simply solving the system, but that solving the system is several
times faster than constructing the inverse matrix. You will also see
that matrices with special formats, such as tridiagonal matrices,
can be solved very efficiently. And you will see even simple
matrices can be difficult to numerically invert.
You will be measuring elapsed time in order to see how long these calculations take. The problem sizes are designed to take a modest amount of time (less than 6 minutes) on newer computers.
WARNING: Most newer computers have more than one processor (core). By default, Matlab will use all the processors available by assigning one ``thread'' to each available processor. This procedure will mess up our timings, so you should tell Matlab to use only a single thread. To do this, you should start up Matlab with the command line
matlab -singleCompThreadIf you do not know how to start up Matlab from the command line, use the following command at the beginning of your session.
maxNumCompThreads(1);Matlab will warn you that this command will disappear in the future, but it should work fine now.
Matlab provides the commands tic and toc to measure computational time. The tic command starts the stopwatch, and the toc command stops it, either printing the elapsed time or returning its value as in the expression elapsedTime=toc;. The times are in seconds. (Note: tic and toc measure elapsed time. When a computer is doing more than one thing, the cputime function can be used to measure how much computer time is being used for this task alone.)
function elapsedTime=exer1(n)
% elapsedTime=exer1(n)
% comments
% your name and the date
if mod(n,2)==0
error('Please use only odd values for n');
end
A = magic(n); % only odd n yield invertible matrices
b = ones(n,1); % the right side vector doesn't change the time
tic;
Ainv = ??? % compute the inverse matrix
xSolution = ??? % compute the solution
elapsedTime=toc;
Time to compute inverse matrices n time ratio 161 _________ 321 _________ _________ 641 _________ _________ 1281 _________ _________ 2561 _________ _________ 5121 _________ _________ 10241 _________ _________
x=A\b;It may help you to remember this operator if you think of the A as being ``underneath'' the slash. The effect of this operator is to find the solution of the system of equations A*x=b.
The backslash looks strange, but there is a method to this madness. You might wonder why you can't just write x=b/A. This would put the column vector b to the left of the matrix A and that is the wrong order of operations.
Time to compute solutions n time ratio 161 _________ 321 _________ _________ 641 _________ _________ 1281 _________ _________ 2561 _________ _________ 5121 _________ _________ 10241 _________ _________
Comparison of times n (time for inverse)/(time for solution) 161 _________ 321 _________ 641 _________ 1281 _________ 2561 _________ 5121 _________ 10241 _________
You should be getting the message: ``You should never compute an inverse when all you want to do is solve a system.''
Warning: the ``\'' symbol in Matlab will work
when the matrix A is not square. In fact, sometimes it
will work when A actually is a vector. The results are not usually
what you expect and no error message is given. Be careful of this potential
for error when using ``\''. A similar warning is true
for the / (division) symbol because Matlab will try to
``interpret'' it if you use it with matrices or vectors and you
will get ``answers'' that are not what you intend.
Time to compute solutions Size time ratio 10240 ________ _______ 102400 ________ _______ 1024000 ________ _______ 10240000
N=10; A = dif2(N); xKnown = sqrt( (1:N)' ); b = ??? % compute the right side corresponding to xKnown xSolution = ??? % compute the solution using "\" err=norm(xSolution-xKnown)/norm(xKnown)
dif2 matrix
size error determinant cond. no.
10 _________ __________ __________
40 _________ __________ __________
160 _________ __________ __________
The dif2 matrix is about as nicely behaved as a matrix can be.
It is neither close to singular nor difficult to invert.
Hilbert matrix
size error determinant cond. no.
10 _________ __________ __________
15 _________ __________ __________
20 _________ __________ __________
The Hilbert matrix is so close to being singular that numerical approximations
cannot distinguish it from a singular matrix.
Frank matrix
size error determinant cond. no.
10 _________ __________ __________
15 _________ __________ __________
20 _________ __________ __________
The Frank matrix can be proved to have a determinant equal to 1.0 because
its eigenvalues come in
Pascal matrix
size error determinant cond. no.
10 _________ __________ __________
15 _________ __________ __________
20 _________ __________ __________
The Pascal matrix is another matrix that has a determinant of 1, with
eigenvalues occurring in
In the following sections, you will write your own routine that does the same task as the Matlab ``\'' command.
The standard method for computing the inverse of a matrix is Gaußian elimination. You already know this algorithm, perhaps by another name such as row reduction. You have seen it discussed in class and you can find a discussion on the web at, for example, http://en.wikipedia.org/wiki/Gaussian_elimination .
First, we will prefer to think of the process as having two separable parts, the ``factorization'' or ``forward substitution'' and ``back substitution'' steps. The important things to recall include:
Different methods for choosing pivots lead to different variants of Gauß factorization. Important ones include:
We now turn to writing code for the Gauß factorization. The discussion in this lab assumes that you are familiar with Gaußian elimination (sometimes called ``row reduction''), and is entirely self-contained. Because, however, interchanging rows is a source of confusion, we will assume at first that no row interchanges are necessary.
The idea is that we are going to use the row reduction operations
to turn a given matrix ![]() into an upper triangular matrix
(all of whose elements below the main diagonal are
zero)
into an upper triangular matrix
(all of whose elements below the main diagonal are
zero) ![]() and at the same time keep track of the multipliers
in the lower triangular matrix
and at the same time keep track of the multipliers
in the lower triangular matrix ![]() . These matrices will be
built in such a way that
. These matrices will be
built in such a way that ![]() could be reconstructed
from the product
could be reconstructed
from the product ![]() at any time during the factorization
procedure.
at any time during the factorization
procedure.
Alert: The fact that
![]() even before the
computation is completed can be a powerful debugging technique. If you
get the wrong answer at the end of a computation, you can test each
step of the computation to see where it has gone wrong. Usually you
will find an error in the first step, where the error is easiest to
understand and fix.
even before the
computation is completed can be a powerful debugging technique. If you
get the wrong answer at the end of a computation, you can test each
step of the computation to see where it has gone wrong. Usually you
will find an error in the first step, where the error is easiest to
understand and fix.
Let's do a simple example first. Consider the matrix
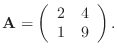
There is only one step to perform in the row reduction process: turn the 1 in the lower left into a 0 by subtracting half the first row from the second. Convince yourself that this process can be written as
If you want to write,
![]() , you need to have
, you need to have
![]() be the inverse of the first matrix on the left
in (2). Thus
be the inverse of the first matrix on the left
in (2). Thus
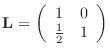
and
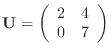
are matrices that describe the row reduction step (
Now, suppose you have a 5 by 5 Hilbert matrix (switching to Matlab notation) A, and you wish to perform row reduction steps to turn all the entries in the first column below the first row into zero, and keep track of the operations in the matrix L and the result in U. Convince yourself that the following code does the trick.
n=5; Jcol=1; A=hilb(5); L=eye(n); % square n by n identity matrix U=A; for Irow=Jcol+1:n % compute Irow multiplier and save in L(Irow,Jcol) L(Irow,Jcol)=U(Irow,Jcol)/U(Jcol,Jcol); % multiply row "Jcol" by L(Irow,Jcol) and subtract from row "Irow" % This vector statement could be replaced with a loop U(Irow,Jcol:n)=U(Irow,Jcol:n)-L(Irow,Jcol)*U(Jcol,Jcol:n); end
function [L,U]=gauss_lu(A) % function [L,U]=gauss_lu(A) % performs an LU factorization of the matrix A using % Gaussian reduction. % A is the matrix to be factored. % L is a lower triangular factor with 1's on the diagonal % U is an upper triangular factor. % A = L * U % your name and the date
It turns out that omitting pivoting leaves the function you just wrote vulnerable to failure.
A1 = [ -2 1 0 0 0
1 0 1 -2 0
0 0 0 1 -2
1 -2 1 0 0
0 1 -2 1 0]
The method should fail for this matrix, producing matrices with
infinity (inf) and ``Not a Number'' (NaN) in them.
In Gaußian elimination it is entirely possible to end up with a zero on the diagonal, as the previous exercise demonstrates. Since you cannot divide by zero, the procedure fails. It is also possible to end up with small numbers on the diagonal and big numbers off the diagonal. In this case, the algorithm doesn't fail, but roundoff errors can overwhelm the procedure and result in wrong answers. One solution to these difficulties is to switch rows and columns around so that the largest remaining entry in the matrix ends up on the diagonal. Instead of this ``full pivoting'' strategy, it is almost as effective to switch the rows only, instead of both rows and columns. This is called ``partial pivoting.'' In the following section, permutation matrices are introduced and in the subsequent section they are used to express Gaußian elimination with partial pivoting as a ``PLU'' factorization.
In general, a matrix that looks like the identity matrix but with two rows interchanged is a matrix that causes the interchange of those two rows when multiplied by another matrix. A permutation matrix can actually be a little more complicated than that, but all permutation matrices are products of matrices with a single interchanged pair of rows.
P1=[1 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1];
P2=[1 0 0 0
0 0 0 1
0 0 1 0
0 1 0 0];
You already have written gauss_lu.m to do Gauß eliminiation without pivoting. Now, you are going to add pivoting to the process. The previous section should have convinced you that pivoting is the same thing as multiplying by a permutation matrix. Just as in gauss_lu.m, where you started out with L equal to the identity matrix and saved the row operations in it, you will start off with a permutation matrix P=eye(n) and save the row interchanges in it.
function [P,L,U]=gauss_plu(A)and change the comments to describe the new output matrix P.
% First, choose a pivot row by finding the largest entry
% in column=Jcol on or below position k=Jcol.
% The row containing the largest entry will then be switched
% with the current row=Jcol
[ colMax, pivotShifted ] = max ( abs ( U(Jcol:n, Jcol ) ) );
% The value of pivotShifted from max needs to be adjusted.
% See help max for more information.
pivotRow = Jcol+pivotShifted-1;
if pivotRow ~= Jcol % no pivoting if pivotRow==Jcol
U([Jcol, pivotRow], :) = U([pivotRow, Jcol], :);
L([Jcol, pivotRow], 1:Jcol-1)= L([pivotRow, Jcol], 1:Jcol-1);
P(:,[Jcol, pivotRow]) = P(:,[pivotRow, Jcol]);
end
The reason that pivotShifted must be adjusted to get
pivotRow is because, for example, if J(jcol+1,jcol)
happens to be the largest entry in the column, then the max
function will return pivotShifted=2, not
pivotShifted=(jcol+1).
This is because (jcol+1) is the second entry in the
vector (Jcol:n).
% TEMPORARY DEBUGGING CHECK
if norm(P*L*U-A,'fro')> 1.e-12 * norm(A,'fro')
error('If you see this message, there is a bug!')
end
We have seen how to factor a matrix ![]() into the form:
into the form:
where
Let's consider the factored linear system once more.
It helps to make
up some names for variables and look at the problem in a different way:
In summary, the PLU Solution Algorithm is:
To solve
![]() after finding the factors
after finding the factors
![]() ,
, ![]() ,
, ![]() and the right hand side
and the right hand side ![]() ,
,
Ouch! I promised a simple algorithm, but now instead of having to solve one system, we have to solve three, and we have three different solution vectors running around. But things actually have gotten better, because these are really simple systems to solve:
P = [0 1 0
0 0 1
1 0 0];
L = [1 0 0
0.5 1 0
0.25 0.5 1];
U = [4 4 8
0 4 8
0 0 2];
confirm that
Step
0 b = [ 28; 18 ; 16 ]
1 z = [ __________; __________ ; __________ ]
2 y = [ __________; __________ ; __________ ]
3 x = [ __________; __________ ; __________ ]
In the following exercise, you will be writing a routine plu_solve.m, to solve the linear system (1) by solving the permutation, lower and upper triangular systems. Because this is a three stage process, we will divide it into four separate m-files: u_solve.m, l_solve.m, p_solve.m, and plu_solve.m. The plu_solve routine will look like:
function x = plu_solve ( P, L, U, b ) % function x = plu_solve ( P, L, U, b ) % solve a factored system % P=permutation matrix % L=lower-triangular % U=upper-triangular % b=right side % x=solution % your name and the date % Solve P*z=b for z using p_solve z = p_solve(P,b); % Solve L*y=z for y using l_solve y = l_solve(L,z); % Solve U*x=y for x using u_solve x = u_solve(U,y);
function z=p_solve(P,b) % z=p_solve(P,b) % P is an orthogonal matrix % b is the right hand side % z is the solution of P*z=b % your name and the date z= ???
function y=l_solve(L,z)
% y=l_solve(L,z)
% L is a lower-triangular matrix whose diagonal entries are 1
% z is the right hand side
% y is the solution of L*y=z
% your name and the date
% set n for convenience and simplicity
n=numel(z);
% initialize y to zero and make sure it is a column vector
y=zeros(n,1);
% first row is really an easy one, especially since the diagonal
% entries of L are equal to 1
Irow=1;
y(Irow)=z(Irow);
for Irow=2:n
rhs = z(Irow);
for Jcol=1:Irow-1
rhs = rhs - ???
end
y(Irow) = ???
end
function x = u_solve(U,y)
% x=u_solve(U,y)
% U is an upper-triangular matrix
% y is the right hand side
% x is the solution of U*x=y
% your name and the date
% set n for convenience and simplicity
n=numel(y);
% initialize y to zero and make sure it is a column vector
x=zeros(n,1);
% last row is the easy one
Irow=n;
x(Irow)=y(Irow)/U(Irow,Irow);
% the -1 in the middle means it is going up from the bottom
for Irow=n-1:-1:1
rhs = y(Irow);
% the following loop could also be written as a single
% vector statement.
for Jcol=Irow+1:n
rhs = rhs - ???
end
x(Irow) = ???
end
x = plu_solve(P,L,U,b)for the matrices and right side vector in the previous exercise. Double-check your work by showing
relErr = norm(P*L*U*x-b)/norm(b)is zero or roundoff.
A = rand(100,100); x = rand(100,1); b = A*x;and the rest of the code as in the previous part of this Exercise. The error relErr will usually be a roundoff sized number. There is always some chance that the randomly generated matrix A will end up poorly conditioned or singular, though. If that happens, generate A and x again: they will be different this time.
You might wonder why we don't combine the m-files gauss_plu.m
and plu_solve.m into a single routine. One reason is that there
are other things you might want to do with the factorization instead
of solving a system. For example, one of the best ways of computing a
determinant is to factor the matrix. (The determinant of any permutation
matrix is ![]() , the determinant of L is 1 because L has
all diagonal entries equal to 1, and the determinant of U is
the product of its diagonal entries.) Another reason is that the
factorization is much more expensive (i.e., time-consuming)
than the solve is, and you might be able to solve the system many
times using the same factorization. This latter case is presented
in the following section.
, the determinant of L is 1 because L has
all diagonal entries equal to 1, and the determinant of U is
the product of its diagonal entries.) Another reason is that the
factorization is much more expensive (i.e., time-consuming)
than the solve is, and you might be able to solve the system many
times using the same factorization. This latter case is presented
in the following section.
You saw how to numerically solve certain ordinary differential equations in Labs 1-4. You saw that you could solve a scalar linear ODE using the backward Euler method but for nonlinear and for systems of equations, you used Newton's method to solve the timestep equations. It turns out that linear systems can be solved using matrix solution methods without resort to Newton's method. At each time step in that solution, you need to solve a linear system of equations, and you will use plu_factor and plu_solve for this task. You will also see the advantage of splitting the solution into a ``factor'' step and a ``solve'' step.
Consider a system of ordinary differential equations.
In Matlab, we will represent the vector
![]() as
u(:,k).
as
u(:,k).
The following code embodies the procedure described above. Copy it
into a script m-file called bels.m (for Backward Euler
Linear System). This particular system, using the negative of the
dif2 matrix, turns out to be a discretization of the
time-dependent heat equation. The variable
![]() represents
temperature and is a function of time and also of a
one-dimensional spatial variable
represents
temperature and is a function of time and also of a
one-dimensional spatial variable ![]() for fixed
for fixed ![]() .
The plot is a compact way to illustrate the vector
.
The plot is a compact way to illustrate the vector
![]() with its subscript measured along the horizontal axis.
The red line is the initial shape, the green line is what the final
limiting shape would be if integration were continued to
with its subscript measured along the horizontal axis.
The red line is the initial shape, the green line is what the final
limiting shape would be if integration were continued to ![]() ,
and the blue lines are the shapes at intermediate times.
,
and the blue lines are the shapes at intermediate times.
% ntimes = number of temporal steps from t=0 to t=1 . ntimes=30; % dt = time increment dt=1/ntimes; t(1,1)=0; % N is the dimension of the space N=402; % initial values u(1:N/3 ,1) = linspace(0,1,N/3)'; u(N/3+1:2*N/3,1) = linspace(1,-1,N/3)'; u(2*N/3+1:N,1) = linspace(-1,0,N/3)'; % discretization matrix is -dif2 multiplied % by a constant to make the solution interesting A= -N^2/5 * dif2(N); EulerMatrix=eye(N)-dt*A; tic; for k = 1 : ntimes t(1,k+1) = t(1,k) + dt; [P,L,U] = gauss_plu(EulerMatrix); u(:,k+1) = plu_solve(P,L,U,u(:,k)); end CalculationTime=toc % plot the solution at sequence of times plot(u(:,1),'r') hold on for k=2:3:ntimes plot(u(:,k)) end plot(zeros(size(u(:,1))),'g') title 'Solution at selected times' hold off
You should be aware that the system matrix in this exercise is sparse, but we have not taken advantage of that fact here. Neither have we taken advantage of the fact that the matrix is symmetric and positive definite (so that pivoting is unnecessary). As you have seen, a lot of time could be saved by using gallery(tridiag,n) and sparse forms of P, L, and U.
If you happened to try Exercise 11 using the ``\'' form, you would find that it is substantially faster than our routines. It is faster because it takes advantage of programming efficiencies that are beyond the scope of the course, not because it uses different methods. One such efficiency would be the replacement of as many loops as possible with vector statements.
[ colMax, pivotShifted ] = max ( abs ( U(Jcol:n, Jcol ) ) );
pivotRow = Jcol+pivotShifted-1;
if pivotRow ~= Jcol % no pivoting if pivotRow==Jcol
U([Jcol, pivotRow], :) = U([pivotRow, Jcol], :);
L([Jcol, pivotRow], 1:Jcol-1)= L([pivotRow, Jcol], 1:Jcol-1);
P(:,[Jcol, pivotRow]) = P(:,[pivotRow, Jcol]);
end
In this section, you will write your own code to accomplish the same end.
Note: Given a projection matrix ![]() that represents
a single interchange of two rows, so that
that represents
a single interchange of two rows, so that ![]() results in two rows of
a matrix
results in two rows of
a matrix ![]() being interchanged, then the product
being interchanged, then the product ![]() represents
the interchange of two columns.
represents
the interchange of two columns.
The key to the proof of correctness of the Gauß factorization strategy is
the fact that, at each step, the equality ![]() holds, where
holds, where
Suppose you have completed several steps of the Gauß factorization,
and on the subsequent step have discovered that pivoting is necessary.
Call the pivoting matrix ![]() . Recall that
. Recall that
![]() so that you can write
so that you can write
A = [ 6 1 1 0 1 1
1 6 1 1 0 1
1 1 6 1 1 0
1 1 0 1 1 6
1 0 1 1 6 1
0 1 1 6 1 1 ];
Use your gauss_plu function on this matrix and confirm
that only a single interchange of rows four and six is the result
of the pivoting strategy.
Back to MATH2071 page.