MATH2071: LAB 8: The Eigenvalue Problem

Introduction Exercise 1
Eigenvalues and eigenvectors Exercise 2
The Power Method Exercise 3
The Inverse Power Method Exercise 4
Finding Several Eigenvectors at Once Exercise 5
Using Shifts Exercise 6
The QR Method Exercise 7
Convergence of the QR Algorithm Exercise 8
Extra Credit: Roots of polynomials Exercise 9
  Extra Credit


Introduction

This lab is concerned with several ways to compute eigenvalues and eigenvectors for a real matrix. All methods for computing eigenvalues and eigenvectors are iterative in nature, except for very small matrices. We begin with a short discussion of eigenvalues and eigenvectors, and then go on to the power method and inverse power methods. These are methods for computing a single eigenpair, but they can be modified to find several. We then look at shifting, which is an approach for computing one eigenpair whose eigenvalue is close to a specified value. We then look at the QR method, the most efficient method for computing all the eigenvalues at once. In the extra credit exercise, we see that the roots of a polynomial are easily computed by constructing the companion matrix and computing its eigenvalues.

This lab will take three sessions.


Eigenvalues and eigenvectors

For any square $ N\times N$ matrix $ A$ , consider the equation $ \det(A-\lambda I)=0$ . This is a polynomial equation of degree $ N$ in the variable $ \lambda$ so there are exactly $ N$ complex roots (counting multiplicities) that satisfy the equation. If the matrix $ A$ is real, then the complex roots occur in conjugate pairs. The roots are known as ``eigenvalues'' of $ A$ . Interesting questions include:

In textbook examples, the determinant is computed explicitly, the (often cubic) equation is factored exactly, and the roots ``fall out.'' This is not how a real problem will be solved.

If $ \lambda$ is an eigenvalue of $ A$ , then $ A-\lambda I$ is a singular matrix, and therefore there is at least one nonzero vector $ {\bf x}$ with the property that $ (A-\lambda I){\bf x}={\bf0}$ . This equation is usually written

$\displaystyle A {\bf x} = \lambda {\bf x}.$ (1)

Such a vector is called an ``eigenvector'' for the given eigenvalue. There may be as many as $ N$ linearly independent eigenvectors. In some cases, the eigenvectors are, or can be made into, a set of pairwise orthogonal vectors. If a set of eigenvectors is arranged to form the columns of a matrix $ E$ and the corresponding eigenvalues are arranged as a diagonal matrix $ \Lambda$ , then (1) is written for the whole set of eigenpairs as

$\displaystyle A E = E \Lambda$ (2)

(Notice that $ \Lambda$ appears on the right.)

Interesting questions about eigenvectors include:

In textbook examples, the singular system $ (A-\lambda I){\bf x}={\bf0}$ is examined, and by inspection, an eigenvector is determined. This is not how a real problem is solved either.

Some useful facts about the eigenvalues $ \lambda$ of a matrix $ A$ :


The Rayleigh Quotient

If a vector $ {\bf x}$ is an exact eigenvector of a matrix $ A$ , then it is easy to determine the value of the associated eigenvalue: simply take the ratio of a component of $ (A{\bf x})_k$ and $ {\bf x}_k$ , for any index $ k$ that you like. But suppose $ {\bf x}$ is only an approximate eigenvector, or worse yet, just a wild guess. We could still compute the ratio of corresponding components for some index, but the value we get will vary from component to component. We might even try computing all the ratios, and averaging them, or taking the ratios of the norms. However, the preferred method for estimating the value of an eigenvalue uses the so-called ``Rayleigh quotient.''

The Rayleigh quotient of a matrix $ A$ and vector $ {\bf x}$ is

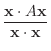$\displaystyle R(A,{\bf x})$ $\displaystyle =$ $\displaystyle \frac{{\bf x}\cdot A{\bf x}}{{\bf x}\cdot{\bf x}}$  
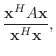  $\displaystyle =$ $\displaystyle \frac{{\bf x}^{H}A{\bf x}}{{\bf x}^{H}{\bf x}},$  

where $ {\bf x}^{H}$ denotes the Hermitian (complex conjugate transpose) of $ {\bf x}$ . The Matlab prime (as in x') actually means the complex conjugate transpose, not just the transpose, so you can use the prime here. (In order to take a transpose, without the complex conjugate, you must use the Matlab function transpose or the prime with a dot as in x.'.) Note that the denominator of the Rayleigh quotient is just the square of the 2-norm of the vector. In this lab we will be mostly computing Rayleigh quotients of unit vectors, in which case the Rayleigh quotient reduces to

$\displaystyle R(A,{\bf x})={\bf x}^{H}A{\bf x}$    for $\displaystyle \vert\vert\mathbf{x}\vert\vert=1. $

If $ \bf x$ happens to be an eigenvector of the matrix $ A$ , the the Rayleigh quotient must equal its eigenvalue. (Plug $ \bf x$ into the formula and you will see why.) When the real vector $ {\bf x}$ is an approximate eigenvector of $ A$ , the Rayleigh quotient is a very accurate estimate of the corresponding eigenvalue. Complex eigenvalues and eigenvectors require a little care because the dot product involves multiplication by the conjugate transpose. The Rayleigh quotient remains a valuable tool in the complex case, and most of the facts remain true.

If the matrix $ A$ is symmetric, then all eigenvalues are real, and the Rayleigh quotient satisfies the following inequality.

$\displaystyle \lambda_{\mbox{min}} \le R(A,{\bf x}) \le \lambda_{\mbox{max}} $

Exercise 1: :
  1. Write an m-file called rayleigh.m that computes the Rayleigh quotient. Do not assume that x is a unit vector. It should have the signature: 
    function r = rayleigh ( A, x )
% r = rayleigh ( A, x )
% comments

% your name and the date
    Be sure to include comments describing the input and output parameters and the purpose of the function.
  2. Copy the m-file eigen_test.m. This file contains several test problems. Verify that the matrix you get by calling A=eigen_test(1) has eigenvalues 1, -1.5, and 2, and eigenvectors [1;0;1], [0;1;1], and [1;-2;0], respectively. That is, verify that $ A{\bf x}=\lambda{\bf x}$ for each eigenvalue $ \lambda$ and eigenvector $ \bf x$ .
  3. Compute the value of the Rayleigh quotient for the matrix A=eigen_test(1) and vectors in the following table. 
           x          R(A,x)       
  [ 3; 2; 1]       4.5
  [ 1; 0; 1]     __________    (is an eigenvector)
  [ 0; 1; 1]     __________    (is an eigenvector)
  [ 1;-2; 0]     __________    (is an eigenvector)
  [ 1; 1; 1]     __________    
  [ 0; 0; 1]     __________
  4. Starting from the vector x=[3;2;1], we are interested in what happens to the Rayleigh quotient when you look at the sequence of vectors $ \mathbf{x}^{(1)}=\mathbf{x}$ , $ \mathbf{x}^{(2)}=\mathbf{Ax}$ , $ \mathbf{x}^{(3)}=\mathbf{A}^2\mathbf{x}$ , $ \ldots$ . Plot the Rayleigh quotients of $ \mathbf{x}^{(k)}=\mathbf{A}^{k-1}\mathbf{x}$ vs. $ k=1,\ldots,25$ . You should observe what appears to be convergence to one of the eigenvalues of $ A$ . Which eigenvalue? Please include your plot along with your summary.

    Note: The superscript $ {}^{(k)}$ in the above expressions does not refer to a power of $ x$ , or to a component. The use of superscript distinguishes it from the $ k^{\mbox{th}}$ component, $ {\bf x}_k$ , and the parentheses distinguish it from an exponent. It is simply the $ k^{\mbox{th}}$ vector in a sequence.

The Rayleigh quotient $ R(A,{\bf x})$ provides a way to approximate eigenvalues from an approximate eigenvector. Now we have to figure out a way to come up with an approximate eigenvector.


The Power Method

In many physical and engineering applications, the largest or the smallest eigenvalue associated with a system represents the dominant and most interesting mode of behavior. For a bridge or support column, the smallest eigenvalue might reveal the maximum load, and the eigenvector represents the shape of the object at the instant of failure under this load. For a concert hall, the smallest eigenvalue of the acoustic equation reveals the lowest resonating frequency. For nuclear reactors, the largest eigenvalue determines whether the reactor is subcritical ($ \lambda<1$ and reaction dies out), critical ($ \lambda=1$ and reaction is sustained), or supercritical ($ \lambda>1$ and reaction grows). Hence, a simple means of approximating just one extreme eigenvalue might be enough for some cases.

The ``power method'' tries to determine the largest magnitude eigenvalue, and the corresponding eigenvector, of a matrix, by computing (scaled) vectors in the sequence:

$\displaystyle {\bf x}^{(k)} = A {\bf x}^{(k-1)} $

Note: As above, the superscript $ {}^{(k)}$ refers to the $ k^{\mbox{th}}$ vector in a sequence. When you write Matlab code, you will typically denote both $ {\bf x}^{(k)}$ and $ {\bf x}^{(k-1)}$ with the same Matlab name x, and overwrite it each iteration. In the signature lines specified below, xold is used to denote $ {\bf x}^{(k-1)}$ and x is used to denote $ {\bf x}^{(k)}$ and all subsequent iterates.

If we include the scaling, and an estimate of the eigenvalue, the power method can be described in the following way.

  1. Starting with any nonzero vector $ \bf x$ , divide by its length to make a unit vector called $ {\bf x}^{(0)}$ ,
  2. $ {\bf x}^{(k)} = (A {\bf x}^{(k-1)})/\vert\vert A {\bf x}^{(k-1)}\vert\vert$
  3. Compute the Rayleigh quotient of the iterate (unit vector) $ r^{(k)} = ({\bf x}^{(k)}\cdot A{\bf x}^{(k)})$
  4. If not done, increment $ k$ and go back to Step 2.

Exercise 2: : Write an m-file that takes a specified number of steps of the power method. Your file should have the signature: 
function  [r, x, rHistory, xHistory] = power_method ( A, x ,maxNumSteps )
% [r, x, rHistory, xHistory] = power_method ( A, x ,maxNumSteps )
% comments

% your name and the date
   .
   .
   .
for k=1:maxNumSteps
   .
   .
   .
   r= ???  %Rayleigh quotient

   rHistory(k)=r;    % save Rayleigh quotient on each step
   xHistory(:,k)=x;  % save one eigenvector on each step
end
On exit, the xHistory variable will be a matrix whose columns are a (hopefully convergent) sequence of approximate dominant eigenvectors. The history variables rHistory and xHistory will be used to illustrate the progress that the power method is making and have no mathematical importance.

Note: It is usually the case that when writing code such as this that requires the Rayleigh quotient, I would ask that you use rayleigh.m, but in this case the Rayleigh quotient is so simple that it is probably better to just copy the code for it into power_method.m.

Using your power method code, try to determine the largest eigenvalue of the matrix eigen_test(1), starting from the vector [0;0;1]. (I have included the result for the first few steps to help you check your code out.) 

  Step     Rayleigh q.    x(1)
  0          -4           0.0               
  1         0.20455     0.12309
  2         2.19403     _____________________________
  3         __________  _____________________________
  4         __________  _____________________________
 10         __________  _____________________________
 15         __________  _____________________________
 20         __________  _____________________________
 25         __________  _____________________________
In addition, plot the progress of the method with the following commands 
plot(rHistory);      title 'Rayleigh quotient vs. k'
plot(xHistory(1,:)); title 'Eigenvector first component vs. k'
Please send me these two plots with your summary.

Exercise 3:

  1. Revise your power_method.m to a new function named power_method1.m with the signature 
    function  [r, x, rHistory, xHistory] = power_method1 ( A, x , tol )
% [r, x, rHistory, xHistory] = power_method1 ( A, x , tol )
% comments

% your name and the date

maxNumSteps=10000;  % maximum allowable number of steps
    You should have an if test with the Matlab return statement in it before the end of the loop. To determine when to stop iterating, add code to effect all three of the following criteria:

    $\displaystyle k$ $\displaystyle >1$    
    $\displaystyle {\vert r^{(k)}-r^{(k-1)}\vert}$ $\displaystyle \leq\epsilon{\vert r^{(k)}\vert}$    and    
    $\displaystyle {\Vert(x^{(k)}-x^{(k-1)})\Vert}$ $\displaystyle \leq\epsilon$    

    where the Matlab variable tol represents $ \epsilon$ . (Recall that $ \Vert x^{(k)}\Vert=1$ .) The second two expressions say that $ r$ and the eigenvector are accurate to a relative error of $ \epsilon$ (the eigenvector is a unit vector). The denominator of the relative error expression multiplies both sides of the inequality so that numerical errors do not cause trouble when $ r$ is small.
    Note: In real applications, it would not be possible to return the history variables because they would require too much storage. Without the history variables a good way to implement this stopping criterion would be to keep track only of $ r^{(k-1)}$ and $ x^{(k-1)}$ in separate variables. Just before you update the values of $ r$ and $ x$ , use Matlab code such as 
    rold=r;  % save for convergence tests
xold=x;  % save for convergence tests
    to save values for $ r^{(k-1)}$ and $ x^{(k-1)}$ .
  2. Since the method should take fewer than maxNumSteps iterations, the method has failed to find an eigenpair if it takes maxNumSteps iterations. Place the statement 
    disp('power_method1: Failed');
    after the loop. Note: normally you would use an error function call here, rather than disp, but for this lab you will need to see the intermediate values in rHistory and xHistory even when the method does not converge at all.
  3. Using your new power method code, try to determine the largest-in-magnitude eigenvalue, and corresponding eigenvector, of the eigen_test matrices by repeatedly taking power method steps. Use a starting vector of all 0's, except for a 1 in the last position, and a tolerance of 1.e-8. Hint: The number of iterations is given by the length of rHistory. If the method does not converge, write ``failed'' in the ``no. iterations'' column. 
    Matrix  Rayleigh q.    x(1)         no. iterations
  1      __________  __________      ____________
  2      __________  __________      ____________
  3      __________  __________      ____________
  4      __________  __________      ____________
  5      __________  __________      ____________
  6      __________  __________      ____________
  7      __________  __________      ____________
    These matrices were chosen to illustrate different iterative behavior. Some converge quickly and some slowly, some oscillate and some don't. One does not converge. Generally speaking, the eigenvalue converges more rapidly than the eigenvector. You can check the eigenvalues of these matrices using the eig function. Plot the histories of Rayleigh quotient and first eigenvector component for all the cases. Send me the plots for cases 3, 5, and 7.

    Matlab hint: The eig command will show you the eigenvectors as well as the eigenvalues of a matrix A, if you use the command in the form: 

    [ V, D ] = eig ( A )
    The quantities V and D are matrices, storing the n eigenvectors as columns in V and the eigenvalues along the diagonal of D.


The Inverse Power Method

The inverse power method reverses the iteration step of the power method. We write:

$\displaystyle A x^{(k)} = x^{(k-1)} $

or, equivalently,

$\displaystyle x^{(k)} = A^{-1} x^{(k-1)} $

In other words, this looks like we are just doing a power method iteration, but now for the matrix $ A^{-1}$ . You can immediately conclude that this process will often converge to the eigenvector associated with the largest-in-magnitude eigenvalue of $ A^{-1}$ . The eigenvectors of $ A$ and $ A^{-1}$ are the same, and if $ {\bf v}$ is an eigenvector of $ A$ for the eigenvalue $ \lambda$ , then it is also an eigenvector of $ A^{-1}$ for $ 1/\lambda$ and vice versa. Naturally, you should not compute $ A^{-1}$ in numerical work, but solve the system instead.

This means that we can freely choose to study the eigenvalue problem of either $ A$ or $ A^{-1}$ , and easily convert information from one problem to the other. The difference is that the inverse power iteration will find us the largest-in-magnitude eigenvalue of $ A^{-1}$ , and that's the eigenvalue of $ A$ that's smallest in magnitude, while the plain power method finds the eigenvalue of $ A$ that is largest in magnitude.

The inverse power method iteration is given in the following algorithm.

  1. Starting with any nonzero vector $ \bf x$ , divide by its length to make a unit vector called $ {\bf x}^{(0)}$ ,
  2. Solve $ A\hat{\bf x} = {\bf x}^{(k-1)}$ , and
  3. Normalize the iterate by setting $ {\bf x}^{(k)}=\hat{\bf x}/\vert\vert\hat{\bf x}\vert\vert$ ;
  4. Compute the Rayleigh quotient of the iterate (unit vector) $ r^{(k)} = ({\bf x}^{(k)}\cdot A{\bf x}^{(k)})$ ; and,
  5. If converged, stop; otherwise, go back to step 2.

Exercise 4: :
  1. Write an m-file that computes the inverse power method, stopping when

    $\displaystyle k>$ $\displaystyle 1$    
    $\displaystyle \vert r^{(k)}-r^{(k-1)}\vert \leq$ $\displaystyle \epsilon \vert r^{(k)}\vert,$    and    
    $\displaystyle \vert\vert x^{(k)}-x^{(k-1)}\vert\vert\leq$ $\displaystyle \epsilon,$    

    where $ \epsilon$ denotes a specified relative tolerance. (Recall that $ \Vert x^{(k)}\Vert=1$ .) This is the same stopping criterion you used in power_method1.m.

    Your file should have the signature: 

    function  [r, x, rHistory, xHistory] = inverse_power ( A, x, tol)
% [r, x, rHistory, xHistory] = inverse_power ( A, x, tol)
% comments

% your name and the date
    Be sure to include a check on the maximum number of iterations (10000 is a good choice) so that a non-convergent problem will not go on forever.
  2. Using your inverse power method code, determine the smallest eigenvalue of the matrix A=eigen_test(2), 
    [r x rHistory xHistory]=inverse_power(A,[0;0;1],1.e-8);
    Please include r and x in your summary. How many steps did it take?
  3. As a debugging check, run 
    [rp xp rHp xHp]=power_method1(inv(A),[0;0;1],1.e-8);
    You should find that r is close to 1/rp, that x and xp are close, and that xHistory and xHp are close. (You should not expect rHistory and 1./rHp to agree in the early iterations.) If these relations are not true, you have an error somewhere. Fix it before continuing. Warning: the two methods may take slightly different numbers of iterations. Compare xHistory and xHp only for the common iterations.

Exercise 5:
  1. Apply the inverse power method to the matrix A=eigen_test(3) starting from the vector [0;0;1] and with a tolerance of 1.e-8. You will find that it does not converge. Even if you did not print some sort of non-convergence message, you can tell it did not converge because the length of the vectors rHistory and xHistory is precisely the maximum number of iterations you chose. In the following steps, you will discover why it did not converge and fix it.
  2. Plot the Rayleigh quotient history rHistory and the first component of the eigenvector history xHistory(1,:). You should find that rHistory seems to show convergence, but xHistory oscillates in a plus/minus fashion, and the oscillation is the cause of non-convergence. Include your plots with your summary. Hint: you may find the plot hard to interpret. Either zoom in or plot only the final 50 or so values.
  3. If a vector $ x$ is an eigenvector of a matrix, then so is $ -x$ , and with the same eigenvalue. The following code will choose the sign of $ x^{(k)}$ so $ x^{(k)}$ and $ x^{(k-1)}$ point in nearly the same direction. This is done by making the dot product of the two vectors positive. If you include it in your inverse_power.m, it will still return an eigenvector, and it will no longer flip signs from iteration to iteration. 
    % choose the sign of x so that the dot product xold'*x >0
factor=sign(xold'*x);
if factor==0
  factor=1;
end
x=factor*x;
  4. Try inverse_power again. It should converge very rapidly.
  5. Fill in the following table with the eigenvalue of smallest magnitude. Start from the vector of zeros with a 1 in the last place, and with a tolerance of 1.0e-8. 
    Matrix  Rayleigh q.    x(1)         no. iterations
  1     __________  __________      ____________
  2     __________  __________      ____________
  3     __________  __________      ____________
  4     __________  __________      ____________
  5     __________  __________      ____________
  6     __________  __________      ____________
  7     __________  __________      ____________
    Be careful! One of these still does not converge. We could use a procedure similar to this exercise to discover and fix that one, but it is more complicated and conceptually similar, so we will not investigate it.


Finding Several Eigenvectors at Once

It is common to need more than one eigenpair, but not all eigenpairs. For example, finite element models of structures often have upwards of a million degrees of freedom (unknowns) and just as many eigenvalues. Only the lowest few are of practical interest. Fortunately, matrices arising from finite element structural models are typically symmetric and negative definite, so the eigenvalues are real and negative and the eigenvectors are orthogonal to one another.

For the remainder of this section, and this section only, we will be assuming that the matrix whose eigenpairs are being sought is symmetric so that the eigenvectors are orthogonal.

If you try to find two eigenvectors by using the power method (or the inverse power method) twice, on two different vectors, you will discover that you get two copies of the same dominant eigenvector. (The eigenvector with eigenvalue of largest magnitude is called ``dominant.'') Working smarter helps, though. Because the matrix is assumed symmetric, you know that the dominant eigenvector is orthogonal to the others, so you could use the power method (or the inverse power method) twice, forcing the two vectors to be orthogonal at each step of the way. This will guarantee they do not converge to the same vector. If this approach converges to anything, it probably converges to the dominant and ``next-dominant'' eigenvectors and their associated eigenvalues.

We considered orthogonalization in Lab 7 and we wrote a function called modified_gs.m. You can use your copy or mine for this lab. You will recall that this function regards the vectors as columns of a matrix: the first vector is the first column of a matrix X, the second is the second column, etc. Be warned that this function will sometimes return a matrix with fewer columns than the one it is given. This is because the original columns were not a linearly independent set. Code for real problems would need to recognize and repair this case, but it is not necessary for this lab.

The power method applied to several vectors can be described in the following algorithm:

  1. Start with any linearly independent set of vectors stored as columns of a matrix $ V$ , use the Gram-Schmidt process to orthonormalize this set and generate a matrix $ V^{(0)}$ ;
  2. Generate the next iterates by computing $ \hat V = AV^{(k-1)}$ ;
  3. Orthonormalize the iterates $ \hat V$ using the Gram-Schmidt process and name them $ V^{(k)}$ ;
  4. Adjust signs of eigenvectors as necessary.
  5. Compute the Rayleigh quotient of the iterates as the diagonal matrix with diagonal equal to the diagonal entries of the matrix $ (V^{(k)})^TAV^{(k)}$ ;
  6. If converged, exit; otherwise return to step 2.

Note: There is no guarantee that the eigenvectors that you find are the ones with largest magnitude eigenvalues! It is possible that your starting vectors were themselves orthogonal to one or more eigenvectors, and you will never recover eigenvectors that are not spanned by the initial ones. In applications, estimates of the inertia of the matrix can be used to mitigate this problem. See, for example, https://en.wikipedia.org/wiki/Sylvester%27s_law_of_inertia for a discussion of inertia of a matrix and how it can be used.

In the following exercise, you will write a Matlab function to carry out this procedure to find several eigenpairs for a symmetric matrix. The initial set of eigenvectors will be represented as columns of a Matlab matrix V.

Exercise 6:
  1. Begin writing a function mfile named power_several.m with the signature 
    function  [R, V, numSteps] = power_several ( A, V , tol )
% [R, V, numSteps] = power_several ( A, V , tol )
% comments

% your name and the date
    to implement the algorithm described above.
  2. Add comments explaining that V is a matrix whose columns represent the eigenvectors and that R is a diagonal matrix with the eigenvalues on the diagonal. Since we are assuming the matrix A to be symmetric, add code to check for symmetry and call Matlab's error function if it is not symmetric.
  3. You can use the following code to make sure the columns of D do not flip sign from iteration to iteration. 
    d=sign(diag(Vold'*V));       % find signs of dot product of columns
D=diag(d);                   % diagonal matrix with +-1
V=V*D;                       % Transform V
  4. Stop the iterations when all three of the following conditions are satisfied.

    $\displaystyle k$ $\displaystyle >1$    
    $\displaystyle \vert\vert R^{(k)}-R^{(k-1)}\vert\vert _{\text{fro}}$ $\displaystyle \leq\epsilon\vert\vert R^{(k)}\vert\vert _{\text{fro}}, \text{ and}$    
    $\displaystyle \vert\vert V^{(k)}-V^{(k-1)}\vert\vert _{\text{fro}}$ $\displaystyle \leq\epsilon\vert\vert V^{(k)}\vert\vert _{\text{fro}}.$    

  5. Add an error message about too many iterations after end of your loop, similar to the ones in power_method1.m and inverse_power.m. You can use Matlab's error function this time.
  6. Test power_several for A=eigen_test(4) starting from the vector of zeros with a 1 in the last place, and with a tolerance of 1.0e-8. It should agree with the results in Exercise 3, up to roundoff.
  7. Run power_several function for the matrix A=eigen_test(4) with a tolerance of 1.0e-8 starting from the vectors 
      V = [ 0  0
        0  0
        0  0
        0  0
        0  1
        1  0];
    What are the eigenvalues and eigenvectors? How many iterations are needed?
  8. Further test your results by checking that the two eigenvectors you found are actually eigenvectors and are orthogonal. (Test that AV=VR is approximately satisfied, where V is your matrix of eigenvectors and R is the diagonal matrix of eigenvalues.)
  9. Since this A is a small ($ 6\times6$ ) matrix, you can find all eigenpairs by using power_several starting from the (obviously linearly independent) vectors 
    V=[0  0  0  0  0  1
   0  0  0  0  1  0
   0  0  0  1  0  0
   0  0  1  0  0  0
   0  1  0  0  0  0
   1  0  0  0  0  0 ];
    What are the six eigenvalues? How many iterations were needed?


Using Shifts

A major limitation of the power method is that it can only find the eigenvalue of largest magnitude. Similarly, the inverse power iteration seems only able to find the eigenvalue of smallest magnitude. Suppose, however, that you want one (or a few) eigenpairs with eigenvalues that are away from the extremes? Instead of working with the matrix $ A$ , let's work with the matrix $ A+\sigma I$ , where we have shifted the matrix by adding $ \sigma$ to every diagonal entry. This shift makes a world of difference.

We already said the inverse power method finds the eigenvalue of smallest magnitude. Denote the smallest eigenvalue of $ A+\sigma I$ by $ \mu$ . If $ \mu$ is an eigenvalue of $ A+\sigma I$ then $ A+\sigma I-\mu I=A-(\mu-\sigma )I$ is singular. In other words, $ \lambda=\mu-\sigma$ is an eigenvalue of $ A$ , and is the eigenvalue of $ A$ that is closest to $ \sigma$ .

In general, the idea of shifting allows us to focus the attention of the inverse power method on seeking the eigenvalue closest to any particular value we care to name. This also means that if we have an estimated eigenvalue, we can speed up convergence by using this estimate in the shift. Although various strategies for adjusting the shift during the iteration are known, and can result in very rapid convergence, we will be using a constant shift.

We are not going to worry here about the details or the expense of shifting and refactoring the matrix. (A real algorithm for a large problem would be very concerned about this!) Our simple-minded method algorithm for the shifted inverse power method looks like this:

  1. Starting with any nonzero vector $ {\bf x}^{(0)}$ , and given a fixed shift value $ \sigma$ :
  2. Solve $ (A-\sigma I)\hat{\bf x} = {\bf x}^{(k-1)}$ , and
  3. Normalize the iterate by setting $ {\bf x}^{(k)}=\hat{\bf x}/\vert\vert\hat{\bf x}\vert\vert$ ; and,
  4. Adjust the eigenvector as necessary.
  5. Estimate the eigenvalue as
    $\displaystyle r^{(k)}$ $\displaystyle =$ $\displaystyle \sigma+ ({\bf x}^{(k)}\cdot (A-\sigma I){\bf x}^{(k)})$  
      $\displaystyle =$ $\displaystyle ({\bf x}^{(k)}\cdot A{\bf x}^{(k)})$  

  6. If converged, exit; otherwise return to step 2.

Exercise 7: Starting from your inverse_power.m, write an m-file for the shifted inverse power method. Your file should have the signature: 
function  [r, x, numSteps] = shifted_inverse ( A, x, shift, tol)
% [r, x, numSteps] = shifted_inverse ( A, x, shift, tol)
% comments

% your name and the date
  1. Compare your results from inverse_power.m applied to the matrix A=eigen_test(2) starting from [0;0;1] and using a relative tolerance of 1.0e-8 with results from shifted_inverse.m with a shift of 0. The results should be identical and take the same number of steps.
  2. Apply shifted_inverse to the same A=eigen_test(2) with a shift of 1.0. You should get the same eigenvalue and eigenvector as with a shift of 0. How many iterations did it take this time?
  3. Apply shifted_inverse.m to the matrix eigen_test(2) with a shift of 4.73, very close to the largest eigenvalue. Start from the vector [0;0;1] and use a relative tolerance of 1.0e-8. You should get a result that agrees with the one you calculated using power_method but it should take very few steps. (In fact, it gets the right eigenvalue on the first step, but convergence detection is not that fast.)
  4. Using your shifted inverse power method code, we are going to search for the ``middle" eigenvalue of matrix eigen_test(2). The power method gives the largest eigenvalue as about 4.73 and the the inverse power method gives the smallest as 1.27. Assume that the middle eigenvalue is near 2.5, start with the vector [0;0;1] and use a relative tolerance of 1.0e-8. What is the eigenvalue and how many steps did it take?
  5. Recapping, what are the three eigenvalues and eigenvectors of A? Do they agree with the results of eig?

In the previous exercise, we used the backslash division operator. This is another example where the matrix could be factored first and then solved many times, with a possible time savings.

The value of the shift is at the user's disposal, and there is no good reason to stick with the initial (guessed) shift. If it is not too expensive to re-factor the matrix $ A-\sigma I$ , then the shift can be reset after each iteration of after a set of n iterations, for n fixed.

One possible choice for $ \sigma$ would be to set it equal to the current eigenvalue estimate on each iteration. The result of this choice is an algorithm that converges at an extremely fast rate, and is the predominant method in practice.


The QR Method

So far, the methods we have discussed seem suitable for finding one or a few eigenvalues and eigenvectors at a time. In order to find more eigenvalues, we'd have to do a great deal of special programming. Moreover, these methods are surely going to have trouble if the matrix has repeated eigenvalues, distinct eigenvalues of the same magnitude, or complex eigenvalues. The ``QR method'' is a method that handles these sorts of problems in a uniform way, and computes all the eigenvalues, but not the eigenvectors, at one time.

It turns out that the QR method is equivalent to the power method starting with a basis of vectors and with Gram-Schmidt orthogonalization applied at each step, as you did in Exercise 6. A nice explanation can be found in Prof. Greg Fasshauer's class notes. http://www.math.iit.edu/~fass/477577_Chapter_11.pdf

The QR method can be described in the following way.

  1. Given a matrix $ A^{(k-1)}$ , construct its QR factorization; and,
  2. Set $ A^{(k)} = RQ$ .
  3. If $ A^{k}$ has converged, stop, otherwise go back to step 1.
The construction of the QR factorization means that $ A^{(k-1)}=QR$ , and the matrix factors are reversed to construct $ A^{(k)}$ .

The sequence of matrices $ A^{(k)}$ is orthogonally similar to the original matrix $ A$ , and hence has the same eigenvalues. This is because $ A^{(k-1)}=QR$ , and $ A^{(k)}=RQ=Q^TQRQ=Q^TA^{(k-1)}Q$ .

In addition, the method can be modified in a way we will not consider here so that it converges to an ``almost'' upper triangular matrix, where the main subdiagonal will have nonzero entries only when there is a complex conjugate pair of eigenvalues.

In Lab 7, you wrote the function gs_factor.m, that uses the modified Gram-Schmidt method to into the product of an orthogonal matrix, Q, and an upper-triangular matrix, R. You will be using this function in this lab. Everything in this lab could be done using the Matlab qr function or your h_factor.m function from Lab 7, but you should use gs_factor for this lab.

Exercise 8:
  1. Recover your gs_factor.m file from Lab 7, or download my copy gs_factor.m.
  2. Write an m-file for the QR method for a matrix A. Your file should have the signature: 
    function  [e,numSteps] = qr_method ( A, tol)
% [e,numSteps] = qr_method ( A, tol)
% comments

% your name and the date
    e is a vector of eigenvalues of A. Since the lower triangle of the matrix $ A^{(k)}$ is supposed to converge, terminate the iteration when

    $\displaystyle \vert\vert A_{\text{lower triangle}}^{(k)}-A_{\text{lower triangl... ...le \epsilon \vert\vert A_{\text{lower triangle}}^{(k)}\vert\vert _{\text{fro}}$

    where $ \epsilon$ is the relative tolerance. You can use tril(A) to recover just the lower triangle of a matrix. Include a check so the number of iterations never exceeds some maximum (10000 is a good choice), and use the Matlab ``error'' function to stop iterating if it is exceeded.
  3. The eigen_test(2) matrix is $ 3\times3$ and we have found its eigenvalues in exercises 3,4, and 7. Check that you get the same values using qr_method. Use a relative tolerance of 1.0e-8.
  4. Try out the QR iteration for the eigen_test matrices except number 5. Use a relative tolerance of 1.0e-8. Report the results in the following table. 
      Matrix   largest & smallest Eigenvalues   Number of steps
  1           _________ _________           _________
  2           _________ _________           _________
  3           _________ _________           _________
  4           _________ _________           _________
  skip no. 5
  6           _________ _________           _________
  7           _________ _________           _________
  5. In case 7, what is the difference between your computed largest eigenvalue and the one from the Matlab eig function? For the smallest eigenvalue? How does the size of these errors compare with the tolerance of 1.0e-8?
  6. Matrix 5 has 4 distinct eigenvalues of equal norm, and the QR method does not converge. Temporarily reduce the maximum number of iterations to 50 and change qr_method.m to print e at each iteration to see why it fails. What happens to the iterates? As with the case of changing signs, it is possible to ``handle'' this case in the code so that it converges, but we will not pursue it here. Return the maximum number of iterations to its large value and make sure nothing is printed each iteration before continuing.

Serious implementations of the QR method do not work the way our version works. The code resembles the code for the singular value decomposition you will see in the next lab and the matrices Q and R are never explicitly constructed. The algorithm also uses shifts to try to speed convergence and ceases iteration for already-converged eigenvalues.

In the following section we consider the question of convergence of the basic QR algorithm.


Convergence of the QR Algorithm

Throughout this lab we have used a very simple convergence criterion, and you saw in the previous exercise that this convergence criterion can result in errors that are too large. In general, convergence is a difficult subject and fraught with special cases and exceptions to rules. To give you a flavor of how convergence might be reliably addressed, we consider the case of the QR algorithm applied to a real, symmetric matrix, $ A$ , with distinct eigenvalues, no two of which are the same in magnitude. For such matrices, the following theorem can be shown.



Theorem Let $ A$ be a real symmetric matrix of order n and let its eigenvalues satisfy

$\displaystyle 0<\vert\lambda_1\vert<\vert\lambda_2\vert<\dots<\vert\lambda_n\vert.$

Then the iterates $ \{A^{(k)}\}$ of the QR method will converge to a diagonal matrix $ D$ whose entries are the eigenvalues of $ A$ . Furthermore,

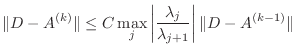
$\displaystyle \Vert D-A^{(k)}\Vert\leq C \max_j \left\vert\frac{\lambda_{j}}{\lambda_{j+1}}\right\vert \Vert D-A^{(k-1)}\Vert$



The theorem points out a method for detecting convergence. Supposing you start out with a matrix $ A$ satisfying the above conditions, and you call the matrix at the $ k^{\mbox{th}}$ iteration $ A^{(k)}$ . If $ D^{(k)}$ denotes the matrix consisting only of the diagonal entries of $ A^{(k)}$ , then the Frobenius norm of $ A^{(k)}-D^{(k)}$ must go to zero as a power of $ \rho=\max\vert\lambda_{j}\vert/\vert\lambda_{j+1}\vert$ , and if $ D$ is the diagonal matrix with the true eigenvalues on its diagonal, then $ D^{(k)}$ must converge to $ D$ as a geometric series with ratio $ \rho$ . In the following algorithm, the diagonal entries of $ A^{(k)}$ (these converge to the eigenvalues) will be the only entries considered. The off-diagonal entries converge to zero, but there is no need to make them small so long as the eigenvalues are converged.

The following algorithm includes a convergence estimate as part of the QR algorithm.

  1. Define $ A^{(0)}=A$ and $ e^{(0)}=$diag$ (A)$ .
  2. Compute $ Q$ and $ R$ uniquely so that $ A^{(k-1)}=QR$ , set $ A^{(k)} = RQ$ and $ e^{(k)}=$diag$ (A^{(k)})$ . (This is one step of the QR algorithm.)
  3. Define a vector of absolute values of eigenvalues $ \lambda^{(k)}=\vert e^{(k)}\vert$ , sorted in ascending order. (Matlab has a function, sort, that sorts a vector in ascending order.) Compute $ \rho^{(k)}=\max_j(\lambda_{j}^{(k)}/\lambda_{j+1}^{(k)})$ . Since the $ \lambda^{(k)}$ are sorted, $ \rho^{(k)}<1$ .
  4. Compute the eigenvalue convergence estimate

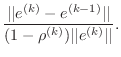
    $\displaystyle \frac{\vert\vert e^{(k)}-e^{(k-1)}\vert\vert}{(1-\rho^{(k)})\vert\vert e^{(k)}\vert\vert}.$

    Return to step 2 if it exceeds the required tolerance.
    Programming hint: Your code should not do a division for this step! If the tolerance value is $ \epsilon$ , your code should check that

    $\displaystyle \vert\vert e^{(k)}-e^{(k-1)}\vert\vert < \epsilon (1-\rho^{(k)})\vert\vert e^{(k)}\vert\vert.$

    The reason is that if $ \rho^{(k)}$ happens to equal 1, there is no division by zero and there is no need to check for that special case.

You may wonder where the denominator $ (1-\rho)$ came from. Consider the geometric series

$\displaystyle S=1+\rho+\rho^2+\rho^3+\dots+\rho^k+\rho^{k+1}+\dots=\frac{1}{(1-\rho)}.$

Truncating this series at the $ (k+1)^{\text{th}}$ term and calling the truncated sum $ S_j$ , we have

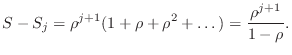
$\displaystyle S-S_j=\rho^{j+1}(1+\rho+\rho^2+\dots)=\frac{\rho^{j+1}}{1-\rho}.$

But, $ \rho^{j+1}=S_{j+1}-S_{j}$ , so

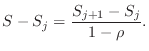
$\displaystyle S-S_j=\frac{S_{j+1}-S_{j}}{1-\rho}.$

Thus, the error made in truncating a geometric series is the difference of two partial sums divided by $ (1-\rho)$ .

Exercise 9:
  1. Copy your qr_method.m file to qr_convergence.m and change the signature line to 
    function [e, numSteps]=qr_convergence(A,tol)
% [e, numSteps]=qr_convergence(A,tol)
% comments

% your name and the date
    Modify the code to implement the above algorithm.
  2. Test your code on eigen_test(1) with a tolerance of 1.e-8. Do the three eigenvalues approximately agree with results from Exercise 8? The number of iterations required might be slightly larger than in Exercise 8.
  3. Apply your algorithm to eigen_test(8), with a tolerance of 1.0e-8. Include the eigenvalues and the number of iterations in your summary.
  4. Compare your computed eigenvalues with ones computed by eig. How close are your eigenvalues? Is the relative error near the tolerance?
  5. If you decrease the tolerance by a factor of ten to 1.0e-9, Does the relative error decrease by a factor of ten as well? This test indicates the quality of the error estimate.
  6. Apply qr_convergence to A=eigen_test(7) with a tolerance of 1.0e-8. How many iterations does it take?
  7. Use eMatlab=eig(A) to compute ``exact'' eigenvalues for eigen_test(7). The entries of eMatlab might not be in the same order, so both should be sorted in order to be compared. What is the relative error 
    norm(sort(e)-sort(eMatlab))/norm(e)
    where e is the vector of eigenvalues from qr_convergence?
  8. How many iterations does qr_method take to reach the relative tolerance of 1.0e-8 for the matrix A=eigen_test(7)? Which convergence method yields more accurate results? If your paycheck depended on achieving a particular accuracy, which method would you use?
  9. Convergence based on provable results is very reliable if the assumptions are satisfied. Try to use your qr_convergence function on the nonsymmetric matrix 
    A = [ .01  1
      -1  .01];
    It should fail. Explain how you know it failed and what went wrong.


Extra Credit: Roots of polynomials (4 points)

Have you ever wondered how all the roots of a polynomial can be found? It is fairly easy to find the largest and smallest real roots using, for example, Newton's method, but then what? If you know a root $ r$ exactly, of course, you can eliminate it by dividing by $ (x-r)$ (called ``deflation''), but in the numerical world you never know the root exactly, and deflation with an inexact root can introduce large errors. Eigenvalues come to the rescue.

Suppose you are given a monic ($ a_1=1$ ) polynomial of degree $ N$

$\displaystyle p(x) = x^N+a_2x^{N-1}+a_3x^{N-2}+\ldots+a_{N}x+\ldots a_{N+1}.$ (3)

Consider the $ N\times N$ matrix with ones on the lower subdiagonal and the negatives of the coefficients of the polynomial in the last column:

$\displaystyle A=\left(\begin{array}{cccccc} 0 & 0 & 0 & \ldots & 0 & -a_{N+1}\\... ...ts & \vdots & \vdots\\ 0 & 0 & 0 & \ldots & 1 & -a_{2}\\ \end{array}\right). $

It is easy to see that $ det(A-\lambda I)=(-1)^Np(\lambda)$ so that the eigenvalues of $ A$ are the roots of $ p$ .

Exercise 10:
  1. Write a Matlab function m-file with signature 
    function r=myroots(a)
% r=myroots(a)
% comments

% your name and the date
    that will take a vector of coefficients and find all the roots of the polynomial $ p(x)$ defined in (3) by constructing the companion matrix and using Matlab's eig function to compute its eigenvalues.
  2. To test myroots, choose at least three different vectors $ r^{(j)}$ of length at least 5. Have at least one of the vectors with complex values. Use the Matlab poly function to find the coefficients of the three polynomials whose roots are the values $ r^{(j)}$ and then use myroots to find the roots of those polynomials. You should find that your computed roots are close to the chosen values in each $ r^{(j)}$ . Please include the three sets of roots and the errors in your computed values in your summary.


Back to MATH2071 page.
kimwong 2019-03-27