parindent 2em setlengthtopmargin0.25in setlengthtextwidth6.25truein setlengthtextheight9truein setlengthoddsidemargin-0.0in setlengthevensidemargin-0.0in setlengthtopmargin-0.5truein newedcommandthmref[1]Theorem ref#1 newedcommandsecref[1]Sref#1 newedcommandlemref[1]Lemma ref#1 newedcommandbAmathbf A newedcommandbFmathbf F newedcommandbXmathbf X newedcommandbYmathbf Y newedcommandbHmathbf H newedcommandbTmathbf T newedcommandbImathbf I newedcommandbumathbf u newedcommandbvmathbf v newedcommandbffmathbf f newedcommandbKmathbf K newedcommandbCmathbf C newedcommandbcmathbf c newedcommandbxmathbf x newedcommandbymathbf y newedcommandbimathbf i newedcommandbamathbf a newedcommandrxhboxrm x newedcommandfHfrak H newedcommandBbRmathbb R newedcommandBbCmathbb C newedcommandcLmathcal L newedcommandvepvarepsilon newedcommandepepsilon newedcommandprobbf (P) newedcommandpropsmathbf S newedcommandbesbegineqnarray newedcommandeesendeqnarray newedcommandbessbegineqnarray* newedcommandeessendeqnarray* newedcommandconemathbf K newedcommandlalangle newedcommandrarangle newedcommandovoverline newedcommandrf[1](ref#1) newedcommandbqbeginequation newedcommandhhrm H^1_0(Omega) newedcommandh^h newedcommandeqendequation newedcommandvvVert newedcommandtritriangle newedcommandpapartial newedcommandnanabla newedcommandfffrac newedcommandvpvarphi newedcommandomOmega newedcommanddedelta newedcommand2rm H^2(Omega) newedcommand3rm H^3(Omega) newedcommandkkrm H^k(Omega) newedcommandalalpha newedcommandam^H newedcommandddpartial newedcommanddbbarpartial_M newedcommandimhboxim newedcommandrehboxre newedcommandisotilde= newedcommandnn[1]left|| #1 right|| newedcommandRmathbbR begintex2html_deferredrenewedcommandtheequationthechapter.arabicequationendtex2html_deferred input psfig.sty begindocument setlengthbaselineskip14pt frontmatter title Math 2950 Lecture Notes:
hspace.5in
bf AN INTRODUCTION TO
hspace0.3in
CONTROL THEORY
hspace0.3in vspace0.3in author
Xinfu Chen (textttxinfu@pitt.edu)
and
Juan Manfredi (textttmanfredi@pitt.edu) datetoday maketitle chapterMATH 2950 SYLLABUS subsection*Lecturers Professors Xinfu Chen and Juan Manfredi. subsection*Prerequisites Calculus and Linear algebra. Basic knowledge on ordinary differential equations (ODE), partial differential equations (PDE), functional analysis will be very helpful, but not mandatory. subsection*Textbooks The will be no textbook. The following will be reserved for your use in the Math library: 1. Richard Bellman, sc Introduction to the Mathematical Theory of Control Processes, Vol I. Academic Press, 1967. 2. Lev Semenovich Pontryagin et. al. it The Mathematical Theory of Optimal Processes, English translation in L.S. sc Pontryagin Selected Works, Volumn 4, Gordon and Breach Science, 1986. 3. L. C. Evans, sc Partial Differential Equations. American Math. Soc. 1998. From time to time, some (perhaps sketchy) course lecture notes will be available through the web pages textttwww.math.pitt.edu/~xfc and textttwww.pitt.edu/~manfredi. subsection*Material to be covered It will be divided into two parts; the first part contains some mathematical tools in functional analysis, ordinary and first order partial differential equations, whereas the second part attributes to the three fundamental topics in theory of optimal control: Euler's calculus of variation, Bellman's dynamic programming, and the Pontryagin's maximum principle. For more details, check the table of contents. subsection*Course requirements There will be several homework sets plus a take home final. Your final grade will be computed as followed:

$$.5\, textrm{Homework grade}+ .5\, textrm{Final grade},$$

where lqlq Homework graderqrq and lqlq Final graderqrq will be normalized to a maximum score of 100. newpage tableofcontents mainmatter setcounterchapter-1 chapterOVERVIEW sectionWhat is an optimal control ? In calculus, we learned to minimize a function with or without constrains. The problem can be stated as follows: Find a such that

ain bA, qquad J(a) = min_{alphain bA} J(alpha)

where bA is a subset of BbR^m (mgeq 1) and J is a (smooth) function from BbR^m to BbR. This minimization problem can be considered as an optimal control when we call alpha it the control, J the it cost, and bA the it admissible controls. If ainbA is a minimum, then a is called an it optimal control and J(a) it the optimal cost. The control theory we consider here generalizes the above minimization in several aspects. First of all, the control alpha will be vector valued functions of time tin[t₀,t₁] subsetBbR to BbRⁿ (ngeq 1). The admissible set will then be a subset bA in some function space bX, say L²((t₀,t₁);BbR^m). For simplicity, we assume that $bA= \{ alpha ; alpha:[t_0,t_1]to A \}$ where A is a set in BbRⁿ. Secondly, the process considered here is to control a it state function y:tin[t₀,t₁]to y(t)in BbRⁿ, say the position and speed of an aircraft at time t. The (physical) state function y is assumed to be it controlable in the sense that it is (uniquely) determined by the control (and the initlal conditions). More precisely, y=y(t) satisfies a system of ordinary differential equations, besdot y:=fracdydt = f(y,alpha)hbox forall tin(t_0,t_1), qquad y(t_0)=xlabel0.odeees where x is a (given) initial state. Typically, the control is taken such that the solution satisfies the additional condition bes y(t_1)in Pilabel0.2 ees where Pi is a (given) subset of BbRⁿ which can be a single point, a line, a polygon, or simply the whole space BbRⁿ. That is to say, it the control alpha needs to transport the state from its initial position x at t=t₀ to a specific state region Pi at a designated terminal time t=t₁ according to the control law dot y=f(y,alpha). Finally, the cost will be a functional J: alphainbXto J(alpha)in BbR. The dependence of J on alpha will be in both a direct and an indirect ways. The indirect dependence is through the state function y, which, as assumed, is uniquely determined by alpha. The dependence of y on x, Pi, t₀, and t₁ will also be an important consideration in both theoretical and practical considerations. Here we focus our attention on those functional J which can be expressed as

$$J(alpha) = J^{(x,t_0,t_1)}(alpha) = int_{t_0}^{t_1} j(y(t),alpha(t)) \, dt$$

where j(y,alpha) is a given function from BbR^n+m to BbR. bf The optimal control problem: Given x,Pi, t₀, and t₁, find an admissible control ainbA that minimize the cost J(alpha) among all alphainbA. begintheorem_type[remark][remark][chapter][][][] The optimal control problem stated is autonomous; namely, t₀ is only a reference point and only the time duration of action T=t₁-t₀ matters. Hence, without of loss, we can often assume that t₀=0. In the general case where f and j depend on t, we can easily make it autonomous by introduce an extra state variable yⁿ⁺¹=t to the original state variable y=(y¹,cdots,yⁿ), and use the differential equation dot yⁿ⁺¹=1 for yⁿ⁺¹. endtheorem_type begintheorem_type[remark][remark][chapter][][][] The functional J can also depend on the final state y(t₁) and control alpha(t₁), e.g.

$$J(alpha) = g(y(t_1),alpha(t_1)) + int_{t_0}^{t_1} j(x(t),alpha(t))\,dt.$$

endtheorem_type begintheorem_type[remark][remark][chapter][][][] When 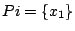$Pi=\{x_1\}$ and jequiv 1, i.e, J(alpha)= t₁-t₀, the optimal control then means to transer the state from x to x₁ in minimal time. This problem is fundamental and is often called the bf time-optimal problem. endtheorem_type When various initial state x and time interval [t₀,t₀+T] are considered, we denote by Psi(x₀,T), called the it optimal cost function, the optimal cost with time duration T and initial position x(t₀)=x; namely,

Psi(x,T) = min_alphainbA J^{(x, 0,T)}(alpha) .

In the sequel, if necessary, we shall write y(t) as y(x,t₀,t₁;t) and a(t) as a(x₀,t₀,t₁; t). Notice that a|_t=t0 is the optimal control to take at the initial time t₀. Namely,

a^*(x,T) = a(x,t₀,t₀+T;t₀)

is the instant optimal control, when the system is at state x and there is time T left. It provides the velocity dot y(t₀)=f(x,a^*) for the system at t=t₀. In control theory, the function a^*(x,T) is called it the optimal policy, which gives a law stating the best control to take when the system is at position x and there is time T left. Correspondingly, an instant control alpha^*=alpha|_t=t0 for alphain bA is called it an admissible policy. sectionAn Example Let's assume that n=1 so y:tin[t₀,t₁]to y(t)inBbR can be considered as the (signed) distance of a particle from its equilibrium position at time t. The control will be the velocity besalpha =dot y.label0.3ees The functional to minimize is bes J(alpha):= int_t_0^t_1 y^2 dt + int_t_0^t_1 alpha^2 dt.label0.4ees The optimal control is to make the best balance between keeping the direct cost low (represented by the second integral) and making the particle stable (i.e. near the equilibrium over the time interval, represented by the first integral).footnote It would be better to understand y as the velocity of a unit mass particle on the real line, and alpha as the force applied. The optimal control is to keep down both the speed y of the particle and the cost resulting from exerting the force alpha. Note that y obeys the ode dot y=alpha and the initial condition y(t₀)=x, which can be solves explicitly:

$$y = cL[alpha] := x + int_{t_0}^t alpha(tau)\, dtau.$$

Here cL is an operator maps alpha to y=cL[alpha]. Let's do not impose any condition on the terminal state y(t₁), i.e., we set Pi=BbR. (Note that part of the control is to make the square integral of y small.) Clearly, for J to be bounded, it is necessary for alpha to be square integrable. Hence, we set

A=BbR,qquad bA=bX := L² ((t₀,t₁); BbR).

We shall display three important approaches for this example. begintheorem_type[exercise][exercise][chapter][][][] Provide an example of a physical situation, which, after reasonable mathematical simplification, leads to a control problem. endtheorem_type sectionCalculus of Variations For every alpha,nuinbX, let's denote by J'[alpha;nu] the directional derivative of J at alpha in the direction of nu; namely,

J'[alpha;nu]:= lim_{vepto 0} fracJ(alpha+vep nu) - J(alpha)vep .

Now suppose that ain bX is an optimal control for the example considered. Then for every nuinbX and vep inBbR, we have a+vepnuinbA so that J(a) geq J(a+vepnu). It then follows that a necessary condition for a to be optimal is

J'[a;nu]=0quad forall nu in bX.

With the simplicity of the problem, we can calculate J'. Set y=cL[a] and $zeta= cL^0[nu]:= int_{t_0}^t nu (tau)\,dtau$. Then the states resulting from the control a and a+vep nu are respectively y and y+vep zeta. Hence, we easily derive that

J'[a;nu]=2int₀^T ( anu + y zeta) dt= 2 int_t0^t₁ ( dot ydot zeta+ y zeta).

Let's make an ansatz that the optimal control a=dot y is differentiable in t. Then, using the integration by parts and the fact that zeta(0)=0 we see that

$$J'[a;nu]= 2dot y(t_1)zeta(t_1) + 2 int_{t_0}^{t_1} ( y-ddot y)zeta \,dt .$$

By taking appropriate direction nu (namely, zeta), one then readilly sees that y=cL[alpha] satisfies the Euler's equation

$$ddot y-y=0 quad forall \, tin (t_0,t_1),qquad y(t_0)=x,quad dot y(t_1)=0.$$

If we differentiate the equation, we then obtain the equation for the optimal control a:

ddot a-a=0quadforall tin(t₀,t₁), qquad dot a(t₀)=x, quad a(t₁)=0.

These systems can be easily solved to give

y= xfrac cosh(t₁-t)cosh (t₁-t₀), qquad a= -xfracsinh(t₁-t)cosh (t₁-t₀).

Note that the solution a is differentiable, not contradicting to our ansatz. Once we find a solution formally, there are many ways to verify it. One way is to use functional analysis tools, which will be introduced in chapter 1. We note that the optimal cost and policy are given by

Psi(x,T)= x² tanh T, qquad a^*(x,T)= -x tanh T.

begintheorem_type[exercise][exercise][chapter][][][] Suppose bA is convex i.e., for every u,vinbA and vepin[0,1], (1-vep)u+vep vin bA. Show that if a is a minimizer of J in bA, then

$$J'[a; nu-a] leq 0 qquad forall\, nuin bA.$$

For the example considered, show that a minimizer, if it exists, is unique. endtheorem_type sectionDynamical Programming The dynamical programming takes a totally different point of view from the calculus of variation. In numerical computations, a continuous process is always approximated by a finite stage process. The dynamical programing originates from the following idea in solving an N+1 stage problem: (1) Pick a guess for the answer for the first stage; (2) From the guess solve the remaining N stage problem; (3) Tune the guess to make it the correct answer. The following derivation is in the continuous version. It would be easier for the reader to consider it in a discretized version. For definiteness, for any given initial position x and time interval [t₀,t₁]. we denote by a=a(x,t₀,t₁;t) and y=y(x,t₀,t₁; t), tin[t₀,t₁], the corresponding the optimal control and the resulting trajectory of the position function. The optimal policy is then given by a^*=a^*(x,T)= a(x₀,t₀,t₀+T;t₀) for all t₀ (since the system is autonomous). A policy can be understood as a decision. Let's fix t₀=0 and t₁=T. Let delta be a small positive constant. At time t=delta, the state will move to the new position hat x= y|_t=delta. It is clear to us that, restricted to tin [delta,t₁], a is an optimal control with initial position hat x and time interval [delta,T]. Indeed, this is the following bf Principle of Optimality: it whatever the initial state and initial decision are, the remaining decision of an optimal policy must constitute an optimal policy with regard to the state resulting from the first decision. In geometry, the principle of optimality can be simply stated as the following: If Q is a point of a geodesic with ending points P and R, the part of the geodesic from Q to R is also a geodesic. Hence, if we can solve a problem for time duration of T-delta for all possible initial data, and if we know hat x, then we can solve the problem for time duration T starting from x. It is important that the optimal policy a^* (initial decision) gives us the approximation

hat x=y|_t=delta=y|_t=0+dot y|_t=0delta+ O(delta²) = x+f(x,a^*) delta+O(delta²).

Now let's apply the principle of optimality, which says

$$Phi(x,T) = int_0^delta j(y,a) \,dt + Phi(hat x,T-delta).$$

Assume that all the functions involved are smooth, and denote by Psi_T and Psi_x the partial derivative of Psi(x,T). Then we can expand bess && Psi(hat x,T-delta) = Psi(x,T) - Psi_T(x,T)delta + Psi_x(x,T) f(x,a^*) delta + O(delta)^2
&& int_0^delta j(y,a)dt = j(x,a^*)delta + O(delta^2).eess Hence, sending deltasearrow 0 we obtain from the principle of optimality that

Psi_T = Psi_x f(x, a^*) + j(x,a^*).

Clearly, since a(x,0,T;cdot) is itself an optimal control, we see that the optimal policy a^* must satisfy

$$Psi_x f(x,a^*) + j(x,a^*) = max_{alphain A} \{ Psi_x f(x,alpha)+ j(x,alpha) \}.$$

In particular, when j(x,alpha)=x²+alpha², we obtain

a^* = -tfrac 12 Psi_x, qquad Psi_T = x² -tfrac 14 Psi_x².

In general, we would have bes Psi_T = H(x,Psi_x)label0.HBJ, ees where Psi_x=(fracpartial Psipartial x¹,cdots,fracpartialPsipartial xⁿ) and H(x,z) is a function from (x,z)inBbR²ⁿ to BbR and is defined by

$$H(x,z) = max_{ alphain A } \{ z cdot f(x,alpha)+ j(x,alpha) \} .$$

where cdot stands for inner product of BbRⁿ, i.e., zcdot f=sum_i=1ⁿ zⁱ fⁱ if z=(z¹,cdots,zⁿ) and f=(f¹,cdots,fⁿ). The PDE we obtained for Psi is called the Bellman or it the Hamilton-Jacobi-Bellman (HBJ) equation. The equation for Phi can be solved by supplying initial condition. Notice that when T=0, i.e., t₁=t₀, we have Psi=0. Hence, for the problem at hand, the HBJ equation is supplied by the initial condition

Psi(x,0)=0, quadforall xinBbR.

One can show that the unique solution is given by

Psi(x,T)=x² tanh T, qquad a^*(x,T)=-tfrac12 Psi_x = -x tanh T.

Clearly, this result coincides with the previous method of calculus of variation. The advantage of dynamical programing is that the vital information in control theory, the optimal cost function and the optimal policy, for all initial states and all time duration, can be obtained at once. We remark that the HBJ equation is a first order PDE whose solution can be generated from solutions to the following Hamiltonian system of odes bes left{beginarray ll dot x = -H_z(x,z)
dot z = H_x(x,z)endarray right. label0.Pees where H_z= (fracpartial Hpartial z¹, cdots, fracpartial Hpartial zⁿ), and similary for H_x. begintheorem_type[exercise][exercise][chapter][][][] Find the corresponding HBJ eqiation when the control is dotalpha=dot y+omega y and the cost density is j(y,alpha)=y²+lambda alpha², where lambda and omega are constants. endtheorem_type sectionThe Pontryagin Maximum Principle Pontryagin, independent of the work of Bellman, obtained a system of odes in essense the same as (ref0.P). To state his result, let's introduce

fH(x,z,alpha) = z cdot f(x,alpha)+ j(x,alpha), qquad H(z,x)= min_{alphain A} fH(x,z,alpha)

begintheorem_type[theorem][theorem][chapter][][][] [Pontryagin Maximum Principle] Let a:[t₀,t₁]to A be an admissable control and rx be the solution to dot rx=f(rx,alpha) with initial condition rx(t₀)=x₀ and satisfying rx(t₁)in Pi. Then in order that a be optimal, it is necessary that there exists a function z(t), t₀leq tleq t₁, such that the following holds: (i) (rx(t),z(t),a(t)), t₀<t<t₁, satisfies besleft{ beginarrayll dot rx = -fH_z(rx,z,a),
dot z = fH_x(rx,z,a),
fH(rx,z,a)=H(rx,z):= inf_alphain bA fH(rx,z,alpha)endarray right.label0.P1 ees (ii) At the end point there holds the transversality condition that z(t₁) is orthogonal to Pi. (iii) At the terminal time t₁, there holds

H(rx(t₁), z(t₁))=fH(rx(t₁),z(t₁),alpha(t₁)) geq 0.

endtheorem_type We remark that if (rx,z,a) satisfies (ref0.P1), then fH(rx(t),z(t),a(t))=H(rx(t),z(t)) is a constant function of t, so that (iii) can be verified at any point tin[t₀,t]. The derivation, even in the formal level, is a little bit technical, and hence is omitted in this overview chapter. Suppose that a is an interior point of bA, then fH_alpha(x,z,a)=0 and hence

H_z=fH_z|_{alpha=alpha^*}, quad H_x = fH_x|_{alpha=alpha^*}

It then follows that (ref0.P) and (ref0.P1) are the same. The advantage of the maximum principle is that (ref0.P1) is always true, whereas (ref0.P) which is used for solving (ref0.HBJ) may face certain difficulties at some singular cases. In application to our model problem, we can easily calculate

fH(x,z,alpha)= x²+alpha² + z alpha, quad H(x,z)= x²- tfrac 14 z².

In addition,

fH(x,z,alpha)=H(x,z)Longleftrightarrow alpha = -tfrac 12 z.

The resulting system (ref0.P1) for (rx,z,a) then becomes

dot rx = tfrac12 z, quadtfrac 12 dot z = rx, quad a= -tfrac 12 z.

Since Pi=BbR, the transversality condition says that z(t₁)=0. Altogether, we see that the solution coincides with that of the calculus of variation. Finally, we mention that the condition (iii) in the maximum principle is indeed equivalent to a second derivative test. begintheorem_type[exercise][exercise][chapter][][][] With f and j as in the example, find H(x,z) when the admissible set is given by (i) A=[-1,1] and (ii) A=[0,1]. endtheorem_type bibliographystyleamsplain bibliographychencite enddocument