Lecture 21: Trees Ch.7.4 Recursion in Linguistic Structure: Trees, Tree Traversal

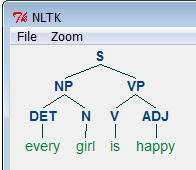
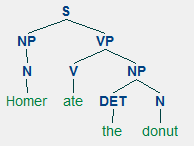
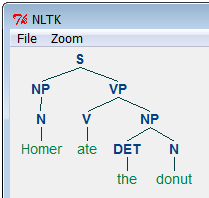
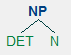
Computational Representation of Syntactic Trees A tree is a set of connected labeled nodes. In linguistics, a sentence or phrase is typically represented as a syntactic tree; "Homer ate the donut" may be syntactically represented as: How can we formally define a syntactic tree? It is important to note that a tree is recursive: a top-level tree is typically composed of multiple subtrees, which are also a tree themselves. (Question: How many subtrees constitute the whole tree above?) A smallest tree, then, looks like the following, which consists of the parent node and a list of child nodes. The individual trees correspond to a single context-free grammar rule: 'NP -> DET N' (left) and 'N -> donut' (right). A tree can also be represented linearly as a text string. In a commonly adopted tree representation scheme below, the label immediately following the opening parenthesis is understood to be the parent node, and the rest its children until the tree is completed by the closing parenthesis. (NP DET N) (N donut) Below are complex trees receiving the same linear representation: (NP DET (N donut)) (NP (DET the) (N donut)) (S (NP (N Homer)) (VP (V ate) (NP (DET the) (N donut)))) For the sake of readability, large trees are often broken down across multiple lines with indentation indicating dominance relation: (S (NP (N Homer)) (VP (V ate) (NP (DET the) (N donut)))) The Tree Object in NLTK (Refer to these NLTK sections: Ch.7.4 Recursion in Linguistic Structure: Trees, Tree Traversal) NLTK has its own implementation of syntactic tree objects called nltk.Tree (same as nltk.tree.tree.Tree). Using its .fromstring() method, you can construct a Tree object by encapsulating a tree string representation. The resulting object is an NLTK Tree object, which is defined as a pair of (1) a single parent node 'NP' and (2) a list of child nodes ['DET', 'N'].   >>> t1 = nltk.Tree.fromstring('(NP DET N)') >>> t1 Tree('NP', ['DET', 'N']) >>> type(t1) <class 'nltk.tree.tree.Tree'> You can print the tree in the form of its string representation using the print command, and as ASCII-style tree drawing with .pretty_print(). In addition, you can call a handy applet .draw() that displays a graphical representation:   >>> print(t1) (NP DET N) >>> t1.pretty_print() NP ___|___ DET N >>> t1.draw() Constructing a more complex syntactic tree can be done in the same way. Note that each of the embedded local trees is formatted as a Tree object:   >>> t2 = nltk.Tree.fromstring('(S (NP (N Homer)) (VP (V ate) (NP (DET the) (N donut))))') >>> t2 Tree('S', [Tree('NP', [Tree('N', ['Homer'])]), Tree('VP', [Tree('V', ['ate']), Tree('NP', [Tree('DET', ['the']), Tree('N', ['donut'])])])]) >>> print(t2) (S (NP (N Homer)) (VP (V ate) (NP (DET the) (N donut)))) >>> t2.pretty_print() S ________|___ | VP | _______|___ NP | NP | | ___|____ N V DET N | | | | Homer ate the donut >>> t2.draw() 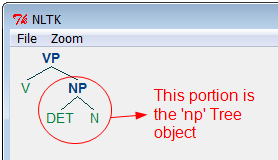Tree objects can also be constructed directly by specifying the parent and the children as two arguments. The former is a single string ('NP'), and the latter is the list data type (['DET', 'N']):   >>> np = nltk.Tree('NP', ['DET', 'N']) # two arguments: parent, children >>> np Tree('NP', ['DET', 'N']) Using this method, you can build up a tree object with smaller component trees:   >>> vp = nltk.Tree('VP', ['V', np]) # np is a Tree object >>> vp Tree('VP', ['V', Tree('NP', ['DET', 'N'])]) >>> vp.draw() 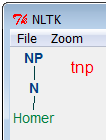Below, both tree-building methods (1. from a string representation using .fromstring(), 2. direct construction) are used.   >>> tnp = nltk.Tree.fromstring('(NP (N Homer))') >>> vpstr = """ (VP (V ate) (NP (DET the) (N donut)))""" >>> tvp = nltk.Tree.fromstring(vpstr) >>> ts = nltk.Tree('S', [tnp, tvp]) # tnp and tvp are Tree objects >>> ts Tree('S', [Tree('NP', [Tree('N', ['Homer'])]), Tree('VP', [Tree('V', ['ate']), Tree('NP', [Tree('DET', ['the']), Tree('N', ['donut'])])])]) >>> print(ts) (S (NP (N Homer)) (VP (V ate) (NP (DET the) (N donut)))) 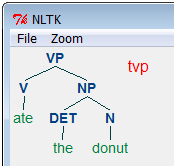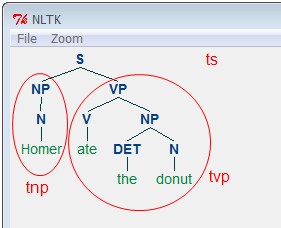NLTK's nltk.Tree is an object class, and it offers its own tree operation methods. Executing dir() on it displays the available methods:   >>> dir(ts) ['__add__', '__class__', '__contains__', '__delattr__', '__delitem__', ... 'append', 'chomsky_normal_form', 'clear', 'collapse_unary', 'convert', 'copy', 'count', 'draw', 'extend', 'flatten', 'freeze', 'fromstring', 'height', 'index', 'insert', 'label', 'leaf_treeposition', 'leaves', 'node', 'pformat', 'pformat_latex_qtree', 'pop', 'pos', 'pprint', 'pretty_print', 'productions', 'remove', 'reverse', 'set_label', 'sort', 'subtrees', 'treeposition_spanning_leaves', 'treepositions', 'un_chomsky_normal_form', 'unicode_repr'] >>> From there, you can try out various methods. Below, .leaves() returns the list of terminal nodes, .height() returns the height of the tree, and .pos() returns a list of POS-tagged words. Lastly, the .append() method appends the specified tree as the rightmost child node.   >>> ts.leaves() # returns terminal node labels, i.e. word tokens ['Homer', 'ate', 'the', 'donut'] >>> ts.height() # returns tree's height 5 >>> ts.pos() # returns word-pos tuples [('Homer', 'N'), ('ate', 'V'), ('the', 'DET'), ('donut', 'N')] >>> adv = nltk.Tree.fromstring('(ADV happily)') # a new adverb subtree >>> ts.append(adv) >>> print(ts) (S (NP (N Homer)) (VP (V ate) (NP (DET the) (N donut))) (ADV happily)) >>> Traversing a tree is done through a recursive function. The user-defined function traverse() in the NLTK section is an example of such functions. Note that the function definition includes a reference to itself. The function recursively traverses a given tree while printing out its nodes. The printed output is the string representation of a tree. Your Turn Build the following tree objects and display them using .pretty_print() and .draw().