Syntactic Ambiguity
The sentence below is ambiguous. How so?
Bart watched a squirrel with binoculars.
In the first, more dominant (or, realistic) meaning, Bart is using binoculars to watch a squirrel. In the second reading, it's the squirrel that is in possession with binoculars. These two interpretations are rooted in two different syntactic configurations:
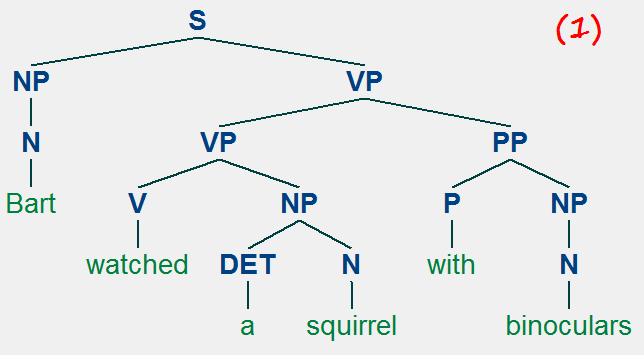
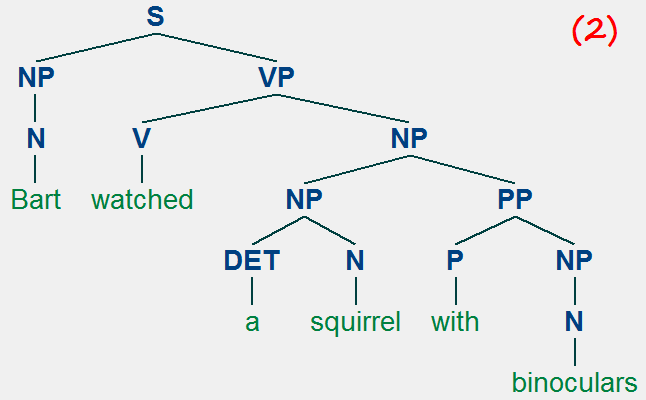
In terms of syntactic tree, reading (1) has the PP "with binoculars" modifying the VP "watched a squirrel", to the effect of "with binoculars" providing additional information on the manner of the watching action. In (2), on the other hand, the PP "with binoculars" is modifying "a squirrel" to create a larger NP "a squirrel with binoculars", meaning it's the squirrel that is in possession of binoculars.
This is a classic example of what is known as PP (preposition phrase) attachment ambiguity, which is rampant in English. As humans, we are good at intuitively screening out "unlikely" syntactic trees, like (2) here -- most of us don't even realize it's possible until we're pushed. But syntactic ambiguities like this abound, especially as sentence gets longer, compounding the job of a parser.
Context-Free Grammar
For a raw sentence to be transformed into a syntactic tree, we need to apply a grammar. Phrase-structure grammar in the form of context-free grammar (CFG) is the standard grammar formalism in many syntactic theories and also language engineering.
In formal language theory (which is coming up in a few weeks), context-free languages are a type of languages that are more complex than regular languages. The theory has three dimensions: (1) automata (FSA, Turing machine, etc.), (2) languages (regular languages, context-free languages, etc.), and finally (3) the grammar. This dimension rounds up the formal language theory, with what is known as the Chomsky Hierarchy (yes, that Chomsky).
Context-free grammar is the grammar formalism that defines the class of context-free languages. It consists of rules of the following type:
Type 2: Each rule is of the form A → ψ
where A is a non-terminal symbol
and ψ consists of any combination of terminal and non-terminal symbols.
A context-free grammar, then, is a set of such CF rules, with a special symbol (S in our case) designated as the start symbol. Below is an example of a context-free grammar:
S -> NP VP
NP -> PRO
NP -> DET N
DET -> 'the'
DET -> 'a'
N -> 'dog'
N -> 'cat'
PRO -> 'she'
VP -> V NP
V -> 'likes'
NLTK's nltk.grammar is the module for handling formal grammars. nltk.CFG, whose original location is nltk.grammar.CFG, implements the context-free grammar. You can create a grammar object using its .fromstring() method, with the grammar rules represented as a multi-line string. The parent node of the very top rule is construed as the start symbol.
| |
>>> grammar2 = nltk.CFG.fromstring("""
S -> NP VP
NP -> PRO | DET N
DET -> 'the' | 'a'
N -> 'dog' | 'cat'
PRO -> 'she'
VP -> V NP
V -> 'likes'
""")
>>> print(grammar2)
Grammar with 10 productions (start state = S)
S -> NP VP
NP -> PRO
NP -> DET N
DET -> 'the'
DET -> 'a'
N -> 'dog'
N -> 'cat'
PRO -> 'she'
VP -> V NP
V -> 'likes'
>>>
| |
Another example can be seen in NLTK's simple grammar example. Note that the grammar notation collapses multiple CFG rules that share the same lefthand-side symbol using the disjunction operator "|". You can see that the returned object grammar2 has a specific grammar object type:
| |
>>> type(grammar2)
<class 'nltk.grammar.CFG'>
|
|
grammar2 has two components: (1) a start symbol, and (2) a list of CF rules. They can be accessed via .start() and .productions():
| |
>>> grammar2.start()
S
>>> grammar2.productions()
[S -> NP VP, NP -> PRO, NP -> DET N, DET -> 'the', DET -> 'a', N -> 'dog',
N -> 'cat', PRO -> 'she', VP -> V NP, V -> 'likes']
|
|
Each item in the list of production rules is a context-free rule. Let's take a closer look. It is NLTK's own special class nltk.grammar.Production, and it comes with its own methods that let us access its inner elements:
| |
>>> srule = grammar2.productions()[0]
>>> srule
S -> NP VP
>>> srule.lhs()
S
>>> srule.rhs()
(NP, VP)
>>> type(srule)
<class 'nltk.grammar.Production'>
>>> srule.is_lexical()
False
>>> vrule = grammar2.productions()[-1]
>>> vrule.lhs()
V
>>> vrule.rhs()
('likes',)
>>> vrule.is_lexical()
True
|
|
You might be wondering: how do I create a rule from scratch? Just like with tree objects, it's a bit of an involved process. A CF rule is made up of a the lefthand side, which is occupied by a non-terminal node object; its right-hand side is occupied by a tuple of objects, each of which is either a non-terminal or a terminal node. You have to build a non-terminal node using a class constructor from the label string; the terminal node can simply be a string.
| |
>>> node1 = nltk.grammar.Nonterminal('ADV')
>>> node1
ADV
>>> type(node1)
<class 'nltk.grammar.Nonterminal'>
>>> rule1 = nltk.grammar.Production(node1, ('happily',))
>>> print(rule1)
ADV -> 'happily'
>>> type(rule1)
<class 'nltk.grammar.Production'>
|
|
Like trees, a grammar can be recursive. A grammar is recursive if a grammatical category is allowed to occur on the left side of a rule as well as on the right hand side. This NLTK section illustrates the concept.
Try Out
Build a context-free grammar called mygrammar that has a coverage sufficient for the sentences below.
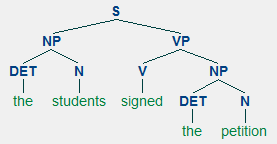
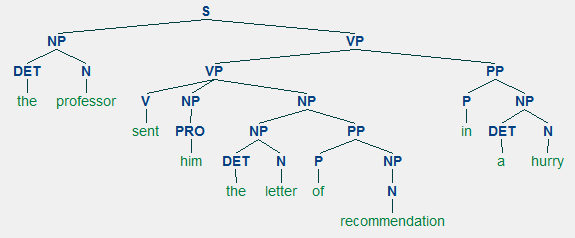
|
Parsing with Context-Free Grammar
(Refer to 8.4 Parsing With Context-Free Grammar)
Once a formal grammar has been defined as a grammar object, it can be used in creating a parser. nltk.RecursiveDescentParser() (seen here) and nltk.ChartParser() (seen here) are methods that create a parser object that utilizes a given grammar, based on two different parsing algorithms.
A parser object created with a supplied grammar can take a tokenized sentence input to produce syntactic trees. In the NLTK book examples (here and here), the .parse() method is called on a parser, which returns a list of trees.
A parser processes input sentences according to the productions of a grammar, and builds one or more constituent structures that conform to the grammar. In this sense, a parser is a procedural interpretation of the grammar applied to the input sentence, for which it utilizes a particular algorithm.
The NLTK book illustrates the following types of parsing algorithms:
- Recursive descent parsing
- top-down algorithm
- pro: finds all successful parses.
- con: inefficient. will try all rules brute-force, even the ones that do not match the input. Goes into an infinite loop when handling a left-recursive rule.
- nltk.RecursiveDescentParser()
- Interactive parsing demo: nltk.app.rdparser()
- Shift-reduce parsing
- bottom-up algorithm
- pro: efficient. only works with the rules that match input words.
- con: may fail to find a legitimate parse even when there is one.
- nltk.ShiftReduceParser()
- Interactive parsing demo: nltk.app.srparser()
- The left-corner parser
- a top-down parser with bottom-up filtering
- nltk.LeftCornerChartParser(): combines left-corner parsing and chart parsing
- Chart parsing
- utilized dynamic programming: builds and refers to well-formed substring tables (WFST)
- pro: efficient.
- con: may take up a big memory space when dealing with a long sentence.
- nltk.ChartParser()
- Interactive parsing demo: nltk.app.chartparser()
Try Out
Using the context-free grammar you built above (mygrammar), make (1) a recursive descent parser and (2) a chart parser and try parsing these sentences:
the professor signed the letter
the students sent the professor the letter in a hurry
|
Treebanks and Grammar
NLTK includes a sample section of the Penn Treebank (3914 sentences and about 10% of the entire corpus), which is a syntactically annotated corpus of English. It can be accessed by nltk.corpus.treebank.parsed_sents(). This example in NLTK book accesses a particular file in the corpus.
Below is the very first sentence of the Treebank corpus. It's possible to print it out and draw the tree diagram.
| |
>>> tr1 = nltk.corpus.treebank.parsed_sents()[0]
>>> tr1
Tree('S', [Tree('NP-SBJ', [Tree('NP', [Tree('NNP', ['Pierre']), Tree('NNP',
['Vinken'])]), Tree(',', [',']), Tree('ADJP', [Tree('NP', [Tree('CD', ['61']),
Tree('NNS', ['years'])]), Tree('JJ', ['old'])]), Tree(',', [','])]), Tree('VP',
[Tree('MD', ['will']), Tree('VP', [Tree('VB', ['join']), Tree('NP', [Tree('DT',
['the']), Tree('NN', ['board'])]), Tree('PP-CLR', [Tree('IN', ['as']), Tree('NP',
[Tree('DT', ['a']), Tree('JJ', ['nonexecutive']), Tree('NN', ['director'])])]),
Tree('NP-TMP', [Tree('NNP', ['Nov.']), Tree('CD', ['29'])])])]), Tree('.', ['.'])])
>>> print(tr1)
(S
(NP-SBJ
(NP (NNP Pierre) (NNP Vinken))
(, ,)
(ADJP (NP (CD 61) (NNS years)) (JJ old))
(, ,))
(VP
(MD will)
(VP
(VB join)
(NP (DT the) (NN board))
(PP-CLR (IN as) (NP (DT a) (JJ nonexecutive) (NN director)))
(NP-TMP (NNP Nov.) (CD 29))))
(. .))
>>> tr1.draw()
>>> tr1.pretty_print()
|
|
Also, you can get the sentence as tokenized words, extract part-of-speech tagged words, and extract the context-free rules used in the tree.
| |
>>> tr1.leaves()
['Pierre', 'Vinken', ',', '61', 'years', 'old', ',', 'will', 'join', 'the', 'board',
'as', 'a', 'nonexecutive', 'director', 'Nov.', '29', '.']
>>> tr1.pos()
[('Pierre', 'NNP'), ('Vinken', 'NNP'), (',', ','), ('61', 'CD'), ('years', 'NNS'),
('old', 'JJ'), (',', ','), ('will', 'MD'), ('join', 'VB'), ('the', 'DT'), ('board',
'NN'), ('as', 'IN'), ('a', 'DT'), ('nonexecutive', 'JJ'), ('director', 'NN'), ('Nov.',
'NNP'), ('29', 'CD'), ('.', '.')]
>>> tr1.productions()
[S -> NP-SBJ VP ., NP-SBJ -> NP , ADJP ,, NP -> NNP NNP, NNP -> 'Pierre', NNP ->
'Vinken', , -> ',', ADJP -> NP JJ, NP -> CD NNS, CD -> '61', NNS -> 'years', JJ ->
'old', , -> ',', VP -> MD VP, MD -> 'will', VP -> VB NP PP-CLR NP-TMP, VB -> 'join',
NP -> DT NN, DT -> 'the', NN -> 'board', PP-CLR -> IN NP, IN -> 'as', NP -> DT JJ NN,
DT -> 'a', JJ -> 'nonexecutive', NN -> 'director', NP-TMP -> NNP CD, NNP -> 'Nov.',
CD -> '29', . -> '.']
|
|
The syntactically annotated corpus is useful in many aspects:
- Linguistic exploration.
You can look up particular syntactic configuration. This example demonstrates how to explore the corpus for cases of a verb taking a sentential complement. This second example is about how to look up "NP VP" or "NP PP" arguments of the verb give.
- Grammar development.
Rather than hand-constructing a context-free grammar, one can simply harvest all CFG rules from the syntactic annotation, applying .productions() on every tree. (Technically, you are piggybacking on other people's work, who already developed a CFG for the annotation process.)
- Development of a weighted grammar.
In addition to the CFG rules themselves, their frequency distribution can be extracted from the annotated corpus: it is then used to induce a probabilistic (=weighted) grammar.
Linguistic Exploration of Trees
In order to explore a tree for a particular syntactic configuration, it is essential that you be able to traverse the subtrees. NLTK's tree object gives you a method for visiting its subtrees: .subtrees(). It returns a generator object, meaning outside of a loop environment you actually won't see the entire list. Using it in a for loop, however, you can reference every subtree in t0, starting with t0 itself and proceeding depth-first. (Note that generator objects are a single-use item, so after using them in a loop they will become empty.)
| |
>>> t0_str = """
(S (NP (N Homer))
(VP (V ate)
(NP (DET the)
(N donut))))
"""
>>> t0 = nltk.Tree.fromstring(t0_str)
>>> t0.subtrees()
<generator object subtrees at 0x03D9EFA8>
>>> for t in t0.subtrees():
print(t)
(S (NP (N Homer)) (VP (V ate) (NP (DET the) (N donut))))
(NP (N Homer))
(N Homer)
(VP (V ate) (NP (DET the) (N donut)))
(V ate)
(NP (DET the) (N donut))
(DET the)
(N donut)
>>>
|
|
In addition, on a tree named t0, the parent node label is accessed via t0.label(), and its child nodes as trees are accessed via t0[0], t0[1], t0[2], etc.
| |
>>> t0.label()
'S'
>>> t0[0]
Tree('NP', [Tree('N', ['Homer'])])
>>> t0[1]
Tree('VP', [Tree('V', ['ate']), Tree('NP', [Tree('DET', ['the']), Tree('N',
['donut'])])])
|
|
Now, you are able to identify all NPs in the tree by going through the subtrees and checking if their parent node is NP:
| |
>>> for t in t0.subtrees():
if t.label() == 'NP': print(t)
(NP (N Homer))
(NP (DET the) (N donut))
|
|
Alternatively, you can return only those subtrees that pass a particular filter test, which is the method used in the NLTK book's examples (here and here). After a filter function is defined on a tree, it can then be used as a parameter while calling .subtrees():
| |
>>> def is_np(t):
return t.label() == 'NP'
>>> for t in t0.subtrees(is_np):
print(t)
(NP (N Homer))
(NP (DET the) (N donut))
|
|
NLTK book has two interesting examples of linguistic exploration: (1) verbs that take a sentential complement, and (2) the verb give taking either "NP NP" ('her the book') or "NP PP" ('the book to my sister') argument. Let's take a close look at the 'give' example. Upcoming Homework 8's (s7) uses the "give NP PP" construction as shown below; the "give NP NP" construction is shown alongside.
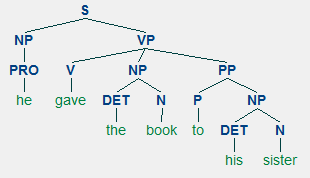
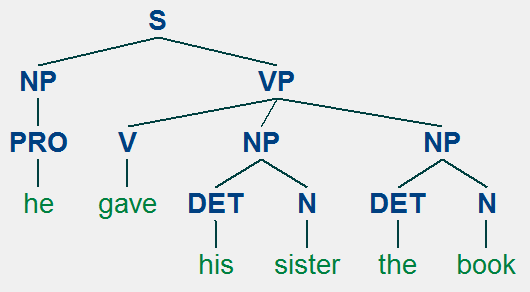
Because our grammar1 from Homework 8 uses PP and not PP-DTV (DTV is for "dative") like in the Penn Treebank, we will modify the definition of give() so it can also work with our grammar1.
| |
>>> def give(t):
return t.label() == 'VP' and len(t) >= 3\
and ('give' in t[0].leaves() or 'gave' in t[0].leaves())\
and t[1].label() == 'NP'\
and (t[2].label().startswith('PP') or t[2].label() == 'NP')
>>> print(t7)
(S
(NP (PRO he))
(VP
(V gave)
(NP (DET the) (N book))
(PP (P to) (NP (DET his) (N sister)))))
>>> for t in t7.subtrees(give):
print(t.label(), "->", end=' ')
for x in t:
print(x.label(), x.leaves(), end=' ')
VP -> V ['gave'] NP ['the', 'book'] PP ['to', 'his', 'sister']
|
|
You are now ready to explore the Penn Treebank corpus for 'give' constructions. We will use the same routine on every Treebank sentence, except for the added line break between each instance.
| |
>>> tb = nltk.corpus.treebank.parsed_sents()
>>> for sent in tb:
for t in sent.subtrees(give):
print(t.label(), "->", end=' ')
for x in t:
print(x.label(), x.leaves(), end=' ')
print()
VP -> VBD ['gave'] NP ['the', 'chefs'] NP ['a', 'standing', 'ovation']
VP -> VBP ['give'] NP ['advertisers'] NP ['discounts', 'for', '*', 'maintaining',
'or', 'increasing', 'ad', 'spending']
VP -> VB ['give'] NP ['it'] PP-DTV ['to', 'the', 'politicians']
VP -> VBD ['gave'] NP ['the', 'answers'] PP-DIR ['to', 'students']
VP -> VBD ['gave'] NP ['them'] NP ['similar', 'help']
VP -> VBP ['give'] NP ['them'] NP ['*T*-1'] PP-TMP ['in', 'the', 'weeks', 'prior',
'to', '*', 'taking', 'standardized', 'achievement', 'tests']
VP -> VB ['give'] NP ['only', 'French', 'history', 'questions'] PP-DTV ['to',
'students', 'in', 'a', 'European', 'history', 'class']
VP -> VB ['give'] NP ['federal', 'judges'] NP ['a', 'raise']
...
|
|
|
|





