


Next: Appendix A: Morris-Lecar
Up: No Title
Previous: Summary
References
- 1
- Baer, S.M., Rinzel, J., and Carrillo. H., 1995,
Analysis of an autonomous phase
model for neuronal parabolic bursting, J. Math. Biology, 33, 309-333.
- 2
- Chay, T.R. and Keizer, J.E., 1983, Minimal model for
membrane oscillations in the pancreatic
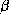 -cell, Biophys. J., 42,
181-190.
-cell, Biophys. J., 42,
181-190.
- 3
- Cole, K.S., Guttman, R., and Bezanilla, F., 1970, Nerve
excitation without threshold, Proc. Nat. Acad. Sci., 65, 884-891.
- 4
- Connor, J.A., Walter, D. and McKown,R., 1977, Neural
repetitive firing: modifications of the Hodgkin-Huxley axon suggested by
experimental results from crustacean axons Biophys.J., 18, 81-102.
- 5
- Doedel, E.J.: 1981, AUTO: A program for the automatic
bifurcation and analysis of autonomous systems, Cong. Num., 30, 265-284.
- 6
- Edelstein-Keshet, L., 1988, Mathematical Models in Biology,
Random House, NY.
- 7
- Destexhe, A., McCormick, D.A., and Sejnowski, T.J., 1993,
A model for 8-10 Hz spindling in interconnected thalamic relay and
reticular neurons, Biophys. J., 65, 2473-2477.
- 8
- Ermentrout, G.B., 1996, Type I membranes, phase
resetting curves, and synchrony, Neural Computation, (in press).
- 9
- Ermentrout, G.B. and Kopell, N., 1991,
Multiple pulse interactions and averaging in systems of coupled neural
oscillators, J. Math. Biology, 29, 195-217.
- 10
- FitzHugh, R., 1960, Thresholds and plateaus in the
Hodgkin-Huxley nerve equations, J. Gen. Physiol., 43, 867-896.
- 11
- FitzHugh, R., 1961, Impulses and physiological states in
models of nerve membrane, Biophys. J. 1, 445-466.
- 12
- FitzHugh, R., 1969, Mathematical models of excitation and
propagation in nerve, in: Biological Engineering, (ed., H.P.Schwan),
McGraw-Hill, NY.
- 13
- Glass, L. and Mackey,M.C., 1988, From Clocks to Chaos: The
Rhythms of Life, Princeton University Press.
- 14
- Goldstein, S.S. and Rall, W., 1974, Changes of action
potential shape and velocity for changing core conductor geometry, Biophys.
J., 14, 731-757.
- 15
- Guttman,R.,Lewis,S. and Rinzel,J., 1980, Control of repetitive
firing in squid axon membrane as a model for a neuroneoscillator, J.
Physiol.(London), 305, 377-395.
- 16
- Hansel, D., Mato, G., and Meunier, C., 1995,
Synchrony in excitatory neural networks, Neural Computation, 7,
307-335.
- 17
- Hayashi, H. and Ishizuka, S., 1992, Chaotic nature
of bursting discharges in the Onchidium pacemaker neuron, J. Theoret. Biol.,
156, 269-291.
- 18
- Hille, B., 1992, Ionic Channels of Excitable Membranes,
2nd edition, Sinauer, Sunderland, MA.
- 19
- Hodgkin,A.L., 1948, The local electric changes
associated with repetitive action in a non-medullated axon, J. Physiol.
(London), 107, 165-181.
- 20
- Hodgkin, A.L. and Huxley, A.F., 1952, A quantitative
description of membrane current and its application to conduction and excitation
in nerve, J. Physiol. (London) 117, 500-544.
- 21
- Kepler, T.B., Abbott, L.F. and Marder, E., 1992,
Reduction of conductance-based neuron models, Biol. Cybern. 66,
381-387.
- 22
- Kopell, N., 1988, Toward a theory of modelling central
pattern generators, in Neural Control of Rhythmic Movements in Vertebrates
(eds., A.H.Cohen, S.Rossignol, and S.Grillner), Wiley, New York.
- 23
- Morris, C. and Lecar,H., 1981, Voltage oscillations in the
barnacle giant muscle fiber, Biophysical J. 35, 193-213.
- 24
- Nagumo, J.S., Arimoto, S., and
Yoshizawa, S., 1962, An active
pulse transmission like simulating nerve axon, Proc. IRE, 50, 2061-2070.
- 25
- Perkel, D.H., Schulman, J.H., Bullock, T.H., Moore, G.P. and
Segundo, J.P., 1964, Pacemaker neurons: effects of regularly spaced synaptic
input, Science, 145, 61-63.
- 26
- Press, W.H., Flannery, B.P., Teukolsky, S.A., and
Vetterling, W.T.,1986, Numerical Recipes: The Art of Scientific Computing,
Cambridge University Press.
- 27
- Rand,R.H. and Armbruster, D., 1987, Perturbation Methods,
Bifurcation Theory, and Computer Algebra. Applied Mathematical Sciences,
65, Springer, New York.
- 28
- Rinzel, J., 1978, On repetitive activity in nerve,
Federation Proc., 37,2793-2802.
- 29
- Rinzel, J., 1985, Excitation dynamics: insights from
simplified membrane models, Federation Proc., 44, 2944-2946.
- 30
- Rinzel, J. and Lee,Y.S., 1987, Dissection of a model
for neuronal parabolic bursting, J. Math. Biol., 25,653-675.
- 31
- Rinzel, J. and Ermentrout, G.B., 1989,
Analysis of neural excitability and oscillations, in:
Methods in Neuronal Modeling: From Synapses to Networks,
(eds., C. Koch and I. Segev), MIT Press, Cambridge MA.
- 32
- Rush, M.E. and Rinzel, J., 1995,
The potassium A-current, low firing rates, and
rebound excitation in Hodgkin-Huxley models,
Bull. Math. Biol., 57, 899-929.
- 33
- Somers, D. and Kopell, N., 1993, Rapid synchronization
through fast threshold modulation, Biol. Cybern., 68, 393-407.
- 34
- Strogatz, S. H., 1994, Nonlinear Dynamics and Chaos,
Addison-Wesley, New York.
- 35
- Traub, R.D. and Miles, R., 1991, Neuronal Circuits of
the Hippocampus, Cambridge University Press, Cambridge,UK.
- 36
- Wang, X.-J. and Rinzel, J., 1995,
Oscillatory and bursting properties
of neurons, in: Handbook
of Brain Theory and Neural Networks, (ed., M.A.Arbib),
MIT Press, Cambridge, MA.
686-691.
- 37
- Wilson, H.R. and Cowan,J.D., 1972, Excitatory and inhibitory
interactions in localized populations of model neurons, Biophys. J., 12,
1-24.
- 38
- Winfree,A.T., 1980, The Geometry of Biological Time,
Biomathematics 8, Springer-Verlag, New York.
Bard Ermentrout
Mon Jul 29 17:47:46 EDT 1996
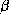 -cell, Biophys. J., 42,
181-190.
-cell, Biophys. J., 42,
181-190.
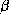 -cell, Biophys. J., 42,
181-190.
-cell, Biophys. J., 42,
181-190.