The researchers point out that mathematicians have focused their attention on two extreme types of networks: "random," where every node is haphazardly connected to a few others ; and "regular," where each node is connected only to its immediate neighbors. "Hands across America," the 1986 demonstration for the homeless in which 7 million people stood hand-in-hand across the country, would be a classic example of a regular network; it would take a long time to pass a message from the East Coast to the West Coast. In a random network all those people would be sitting together in Yankee Stadium and each one would have a telephone connected to about a dozen others scattered around the field.

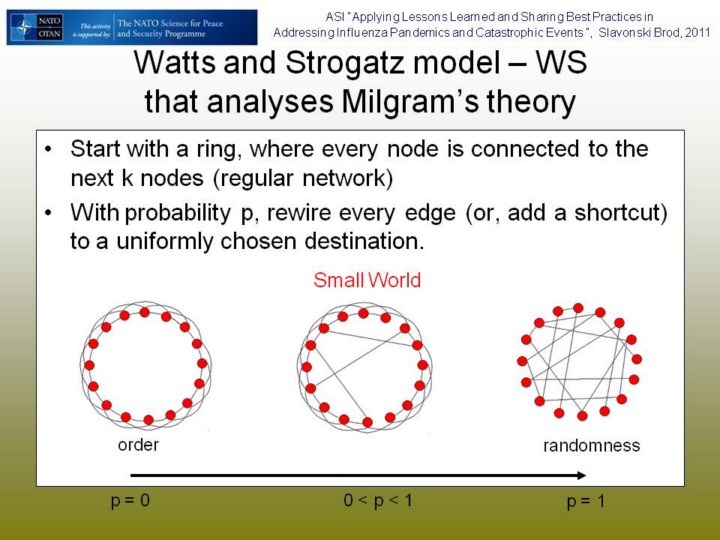
In 1998, Duncan J. Watts and Steven Strogatz from Cornell University published the first network model on the small-world phenomenon. They showed that networks from both the natural and man-made world, such as the neural network of C. elegansand power grids, exhibit the . Watts and Strogatz showed that, beginning with a regular lattice, the addition of a small number of random links reduces the diameter — the longest direct path between any two vertices in the network — from being very long to being very short. The research was originally inspired by Watts' efforts to understand the synchronization of cricket chirps, which show a high degree of coordination over long ranges as though the insects are being guided by an invisible conductor. The mathematical model which Watts and Strogatz developed to explain this phenomenon has since been applied in a wide range of different areas. In Watts' words:[8]

"I think I've been contacted by someone from just about every field outside of English literature. I've had letters from mathematicians, physicists, biochemists, neurophysiologists, epidemiologists, economists, sociologists; from people in marketing, information systems, civil engineering, and from a business enterprise that uses the concept of the small world for networking purposes on the Internet."

Generally, their model demonstrated the truth in Mark Granovetter's observation that it is "the strength of weak ties" that holds together a social network. Although the specific model has since been generalized by Jon Kleinberg, it remains a canonical case study in the field of complex networks. In network theory, the idea presented in the small-world network model has been explored quite extensively. Indeed, several classic results in random graph theory show that even networks with no real topological structure exhibit the small-world phenomenon, which mathematically is expressed as the diameter of the network growing with the logarithm of the number of nodes (rather than proportional to the number of nodes, as in the case for a lattice). This result similarly maps onto networks with a power-law degree distribution, such as scale-free networks.