EXPERIMENT 21/ Solution Kinetics
Method I: Real-time data acquisition
Modified procedure. We will perform the experiment under Condition I; the reactants are stoichiometrically linked (simple second-order kinetics). Initially and for all time, [Pip]t = 2[DNCB]t. Stock solutions of the reactants should be prepared in the following volumes: 25.0 mL of 0.620 M Pip and 100.0 mL of 0.0104 M DNCB in ethanol. Make solutions by weighing out the reagents or use micro-pipets. Dispense ethyl alcohol with syring through the cap.
Simple Second-order Kinetics (modification of procedure on pg. 355-6, Experimental Physical Chemistry by Halpern)
- Turn on the HP8453 without the thermostated cell installed for initialization of the instrument. Note: the glass absorbance cell has a capacity ~6 mL, not 3 mL.
- Set up the spectrometer for kinetics, using an appropriate time interval to not overwhelm you with data in a 45-min scan (longest). Scan Record absorbance data at a wavelength of 472 nm for determining the concentration of DNPP. Scan if different base used.
- Pipet 6.00 mL of the DNCB stock solution into the absorption cell. Turn on the magnetic stirrer and HAAKE thermostated recirculation bath, and let the solution come to thermal equilibrium at 20-25oC. Measure the temperature of the solution with the immersible digital thermometer to ensure equilibration. Use this solution to zero the instrument. Turn off the stirrer before starting the run because it generates artifacts in the data. Do not remove the cell from the holder during the experiment, it is difficult to reposition and will void your blank run. Purge cell using the suction apparatus.
- Begin data acquisition. Inject 200 m L of the Pip solution into this cell using a 0.2-mL Duopette. Notice the marks TC and TD on the Duopette.
DNPP Calibration
- You can use the absorptivity coefficient, e , of DNPP from the lab manual if you record absorbance at 472 nm wavelength.
- The absorbance cell path length must be measured (estimated) on the inside to enable calculation of the concentration of DNPP. See instructor for a micrometer.
Temperature Dependence
- Determine the activation energy and A-factor, and their respective standard deviations, for the reaction by running the above protocol at three or four more temperatures, in addition to the one above. As expected the reaction will proceed significantly faster at higher temperatures. Put a stopper over the cell to prevent evaporation (and odor!) when heating the solution to above room temperature.
Data Analysis (refer to pg. 357 in the lab manual for general discussion, the specifics of the spreadsheet analysis follows.)
- Record the data, following each experimental run, save data on a disk. To save: click on plot data point to convert data to table, under “View” select “Tabulate Selected Spectrum”, then click on “File”, “Print to File”, then save on Drive “a:” as *.txt file.
- Import the data files into Excel spreadsheet as text files, choose “Delimited”, “Space”.
- Add a time column using Series under the Edit menu, after typing in the first two values and highlighting the rest of the column.
- You will perform a nonlinear
least-squares curve fit to determine the parameters [DNPP]o and
k1 according to the nonlinear function (1), (Halpern eq. 12b):
[DNPP]calculated = [DNPP]t = [DNPP]o + [DNCB]o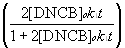
- On the spreadsheet do the above calculation of [DNPP]calculated for each time, in the next column determine the difference:
vertical deviation = [DNPP]observed - [DNPP]calculated
= yI (observed) - yi (calculated) (2)
- The least squares criterion is to find values of [DNPP]o, [DNCB]o, and k1 that minimize the sum of the squares of the vertical deviations of the points from the curve:
![]()
where n is the total number of good points.
- Temporarily assign initial values to [DNPP]o, [DNCB]o, and k1, at the right side of the spreadsheet in separate cells.
- Form a column of y (calculated) using the above equation (1) and the stored values from step 7.
- In the next column compute the vertical deviation in eq. (2).
- In another cell at the bottom of the spreadsheet, compute the sum of the squared deviations.
- The least squares criterion is to find values of [DNPP]o, [DNCB]o, and k1 that minimize the sum of squares. Save graphs as new chart under Chart Wizard.
- Use the Excel tool called Solver (on active sheet only) to find the values of the parameters that minimize the sum of squares. Highlight the cell containing the sum, then invoke Solver. "Set Target Cell" now shows the address containing the sum. Because we want to minimize this sum of squares, click on the "Min" box after "Equal to". Finally, write the cell range containing the parameters to be optimized in the area "By Changing Cells". Select the Option "Assume Non-negative" since the above parameters will be positive numbers.
- Now click the "Solve" button and the program finds the values of [DNPP]o, [DNCB]o, and k1 that minimize the sum of squares.
- If you have not chosen good initial values for the parameters, you may not locate the global minimum sum. There may be a number of local minima. We seek the set of parameters that gives the lowest minimum sum of squares. So, try using a different set of initial parameters and make sure you have found the true global minimum for the sum.
- Plot your data and calculated values on the same graph, and label the data appropriately.