This is a simulation that we did not have time for in the first class.  It illustrates conservation of energy for a case where kinetic energy and potential energy are the only kinds of energy that play a role.



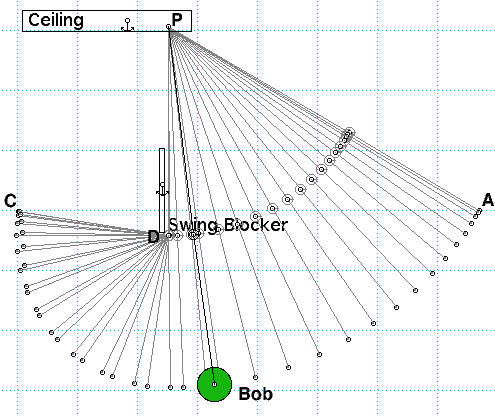
The green pendulum bob is suspended from point P on the ceiling.  It is drawn aside to point A, held at rest, and then released.  It swings down until an obstacle (labelled "Swing Blocker") at D prevents the upper  part of the string from moving any further.  In effect, this converts the pendulum, which was of length PA, into a pendulum of shorter length DC.  The bob continues to point C, and then begins its return journey to point A.  The bob is shown just after it has reached the lowest point of its return swing.  The Ceiling and the Swing Blocker are both kept stationary, as indicated by the small anchor on each of them.  The string PA (or PDC) has a negligible mass, so its kinetic energy can be taken as zero.

At A, total energy = PE + KE = mgh_A + 0   (KE = 0 because the bob is initially at rest.)
At C, total energy = PE + KE = mgh_C + 0   (KE = 0 because the bob is at rest for an instant when it reaches the top of its motion at C.)

By energy conservation, the bob must have the same total energy at C as it had at A.
Therefore    mgh_C + 0 = mgh_A + 0
Consequently     h_C = h<sub>A
The bob rises to the same height at C as it initially had at A.

This happens even though points A and C are not symmetrically related, so it is not an obvious result.  The analysis depends on the rather subtle fact that the force exerted on the bob by the string does no work, and makes no contribution to the potential energy.</sub>