


Next: The isomorphism theorems
Up: No Title
Previous: No Title
A binary operation on a set G is a function from the set product
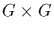 into G. The image of (x,y) is denoted in multiplicative notation
by xy. The operation is associative if
(xy)z=x(yz
) for all x,y,z in
G; it is commutative if xy=yx for all x,y in G. An identity for the
operation is an element 1 in G with the property that x1=
1x=x for
all x in G. [Since e=e1=1, an operation can have at most one
identity.] An inverse of
into G. The image of (x,y) is denoted in multiplicative notation
by xy. The operation is associative if
(xy)z=x(yz
) for all x,y,z in
G; it is commutative if xy=yx for all x,y in G. An identity for the
operation is an element 1 in G with the property that x1=
1x=x for
all x in G. [Since e=e1=1, an operation can have at most one
identity.] An inverse of 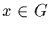 is an element
is an element 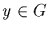 such that
xy=yx=1, provided that the operation on G has an identity. If the
operation is associative and x has an inverse than the inverse is
unique and is denoted by x-1.
such that
xy=yx=1, provided that the operation on G has an identity. If the
operation is associative and x has an inverse than the inverse is
unique and is denoted by x-1.
A group is a set G together with a binary associative operation
which possesses an identity and such that each element of G has an
inverse. The group is Abelian if its binary operation is commutative.
If 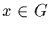 and n is a positive integer, then xn denotes the product of x
with itself n times. Associativity of the operation insures that xn
is well defined. By x-n we understand
(x-1)n. We convene to define
x0 to be 1. It is easy to verify the usual operations with exponents:
and n is a positive integer, then xn denotes the product of x
with itself n times. Associativity of the operation insures that xn
is well defined. By x-n we understand
(x-1)n. We convene to define
x0 to be 1. It is easy to verify the usual operations with exponents:
(xn)(xm)=xn+m=(xm)(xn), and
(xm)n=x
mn
for m and n integers.
A nonempty subset H of G is a subgroup if for each 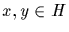 the
element xy is in H, and x-1 is in H. This makes H into a group with
the same identity as G and the same inverses. We write
the
element xy is in H, and x-1 is in H. This makes H into a group with
the same identity as G and the same inverses. We write 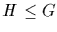 to
indicate that H is a subgroup of G. It is easy to see that
to
indicate that H is a subgroup of G. It is easy to see that
* The intersection of any set of subgroups is a subgroup.
Let S be a subset of G. Define
and call <S> the subgroup of G generated by S. It is the smallest
subgroup of G containing the subset S. An ''internal'' description of
<S> is as follows:
*
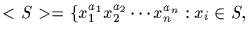 a_
i=1 or -1; n positive integer
a_
i=1 or -1; n positive integer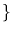
In particular, for 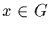 we write <x> for
we write <x> for 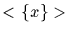 and call <x> the
group generated by the element x. Clearly
and call <x> the
group generated by the element x. Clearly
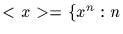 integer
integer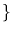 .
A group
G is cyclic if it is generated by one of its elements. The order of
the group G, denoted by
.
A group
G is cyclic if it is generated by one of its elements. The order of
the group G, denoted by
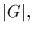 is the cardinality of the set G. For
is the cardinality of the set G. For
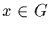 we write
we write
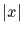 for
for
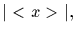 and call
and call
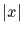 the order of x.
the order of x.
If S and T are subsets of G, we define
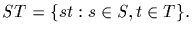 The
set ST is the product of S with T. In particular, we write xS for
The
set ST is the product of S with T. In particular, we write xS for
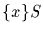 and Ty for
and Ty for 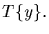 For
For 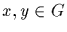 let
xy=yxy
-1. For
let
xy=yxy
-1. For
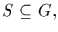
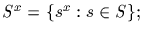 we call Sx the conjugate of set S under x. We
write SG for the set of conjugates
we call Sx the conjugate of set S under x. We
write SG for the set of conjugates
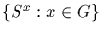 of S under G. Call
of S under G. Call
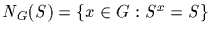 the
normalizer of S in G. The normalizer of
subset S is a subgroup of G. Call
the
normalizer of S in G. The normalizer of
subset S is a subgroup of G. Call
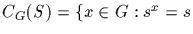 ,
for all
,
for all
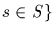 the
centralizer of S in G. The centralizer CG(S) is a
subgroup of G.
the
centralizer of S in G. The centralizer CG(S) is a
subgroup of G.
* Let H and T be subgroups of G. Then
(a) HT is a subgroup if and only if HT=TH
(b)
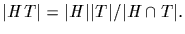
Indeed, assume that HT is a subgroup. Since 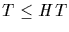 and
and
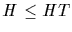 it follows that
it follows that
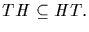 On the other hand, the
map
On the other hand, the
map
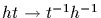 from HT to TH is a bijection showing that
HT=TH. Conversely, assume that HT=TH. Then
from HT to TH is a bijection showing that
HT=TH. Conversely, assume that HT=TH. Then
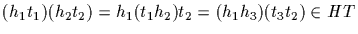 and
and
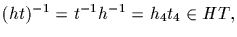 which shows that HT is a
subgroup. As for part (b), note that
h1t1=h2t2 if and
only if
which shows that HT is a
subgroup. As for part (b), note that
h1t1=h2t2 if and
only if
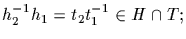 this implies
this implies
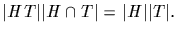
A function
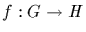 from group G to group H is a
homomorphism if it
preserves the group operations; that is, if
f(xy)=f(x)f(y) for all
from group G to group H is a
homomorphism if it
preserves the group operations; that is, if
f(xy)=f(x)f(y) for all
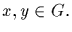 A bijective homomorphism is called an
isomorph
ism. If f is
an isomorphism then
A bijective homomorphism is called an
isomorph
ism. If f is
an isomorphism then
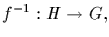 the compositional inverse of f, is also
an isomorphism. We say that G is
isomorphic to H, and write
the compositional inverse of f, is also
an isomorphism. We say that G is
isomorphic to H, and write
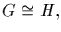 if there is an isomorphism between groups G and H.
Isomorphism is an equivalence relation. We say that H is a
homomorphic image of G if there is a surjective homomorphism from
G to H. An isomorphism of G to itself is called an
au
tomorphism.
The set of automorphisms is a group under the operation of function
composition.
if there is an isomorphism between groups G and H.
Isomorphism is an equivalence relation. We say that H is a
homomorphic image of G if there is a surjective homomorphism from
G to H. An isomorphism of G to itself is called an
au
tomorphism.
The set of automorphisms is a group under the operation of function
composition.
If 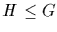 and
and 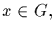 we call xH and Hx cosets of H in G. The set xH
is a left coset and Hx is a right coset. The element x in xH (or Hx)
is called a coset representative.
we call xH and Hx cosets of H in G. The set xH
is a left coset and Hx is a right coset. The element x in xH (or Hx)
is called a coset representative.
Theorem (Lagrange)
If H is a subgroup of G, then
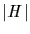 divides
divides
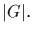
Proof: Consider two cosets of H, g1H and g2H. Observe that they
are either disjoint or identical. Indeed, if
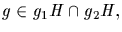 then
g=g1h1=g2h2, for some h1 and h2 in H. Consequently,
g1=gh1-1 and
g2=gh2-1, and therefore
g1H=gh1-1H=gH=gh2-1
H=g2H. We can
therefore write G as the disjoint union of cosets of H, each of
which has cardinality
then
g=g1h1=g2h2, for some h1 and h2 in H. Consequently,
g1=gh1-1 and
g2=gh2-1, and therefore
g1H=gh1-1H=gH=gh2-1
H=g2H. We can
therefore write G as the disjoint union of cosets of H, each of
which has cardinality
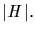 This ends the proof.
This ends the proof.
We denote by G/H the set of (left) cosets of H in G, and call it the
coset space. If
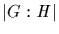 denotes the cardinality of the coset space, by
Lagrange's theorem we know that
denotes the cardinality of the coset space, by
Lagrange's theorem we know that
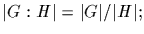 we thus conclude
that
we thus conclude
that
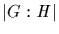 is a divisor of
is a divisor of
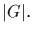 We also call
We also call
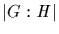 the index of H in
G.
the index of H in
G.
A subgroup H is normal (or
selfconjugate, or invariant) in
G if
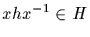 ,
for all
,
for all 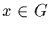 and
and 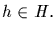 [That is, H is normal in G if
Hx=H, for all
[That is, H is normal in G if
Hx=H, for all 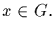 ]
We write
]
We write 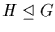 to intimate the fact that
subgroup H is normal in G. If
to intimate the fact that
subgroup H is normal in G. If
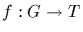 is a group homomorphism, then
the kernel of f is defined by
is a group homomorphism, then
the kernel of f is defined by
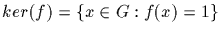 ;
ker(f) is a normal
subgroup of G. The image of f defined by
;
ker(f) is a normal
subgroup of G. The image of f defined by
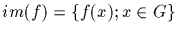 is a
subgroup of T. We also write f(G) for im(f).
is a
subgroup of T. We also write f(G) for im(f).
Observe that 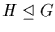 implies
xHx-1=H, or
xH=Hx; thus for a normal subgroup there is no distinction between
left and right cosets.
implies
xHx-1=H, or
xH=Hx; thus for a normal subgroup there is no distinction between
left and right cosets.
* If H is normal in G, then the coset space G/H is made into a
group under the binary operation
(xH)(yH)=xyH.
Indeed,
(xH)(yH)=(xHx-1)(xyH)=H(xyH)=(Hxy)H=xyHH=xyH. The
identity element is H, and x-1H is the inverse of xH
.
The group G/H is called the factor (or quotient) group of G by H.
There is a natural surjective homomorphism
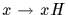 from G to G/H.
Subgroup H is the kernel of this homomorphism.
from G to G/H.
Subgroup H is the kernel of this homomorphism.
* If 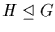 and
and
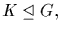 then
then
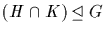 and
and
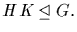 [The
proof is easy.]
[The
proof is easy.]
The direct product
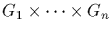 (denoted also
(denoted also
 )
of
groups
)
of
groups
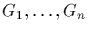 is the group defined on the Cartesian
product
is the group defined on the Cartesian
product
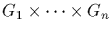 by the operation
by the operation
* Let
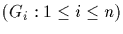 be subgroups of G. The following
statements are equivalent:
be subgroups of G. The following
statements are equivalent:
(1) The map
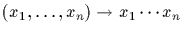 from
from
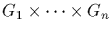 to G
is an isomorphism.
to G
is an isomorphism.
(2)
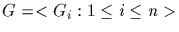 and for each i,
and for each i,
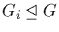 and
and
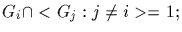
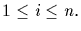
(3) For each i,
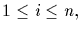
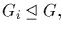 and each
and each 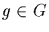 can be
written uniquely as
can be
written uniquely as
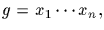 with
with
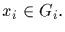
The proof of these equivalences is streightforward.
If any of the above equivalent conditions is satisfied, we
say that G is the direct product of the subgroups
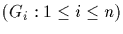 .
.
Observe that if G is the direct product of
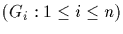 and
and 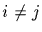 ,
then
xixj=xjxi for all
,
then
xixj=xjxi for all
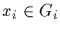 and all
and all
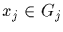 .
[Indeed,
.
[Indeed,
![$x_ix_jx_i^{-1}x_j^{-1}\in (G_i\cap
G_j)=1.]$](img74.gif)



Next: The isomorphism theorems
Up: No Title
Previous: No Title
Gregory Constantine
1998-09-01
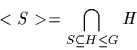
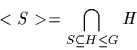
![]() be subgroups of G. The following
statements are equivalent:
be subgroups of G. The following
statements are equivalent:
![]() from
from
![]() to G
is an isomorphism.
to G
is an isomorphism.
![]() and for each i,
and for each i,
![]() and
and
![]()
![]()
![]()
![]() and each
and each ![]() can be
written uniquely as
can be
written uniquely as
![]() with
with
![]()
![]() .
.
![]() and
and ![]() ,
then
xixj=xjxi for all
,
then
xixj=xjxi for all
![]() and all
and all
![]() .
[Indeed,
.
[Indeed,
![]()