


Next: Group actions
Up: No Title
Previous: Definitions and notation
1. If
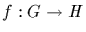 is a homomorphism, then
is a homomorphism, then
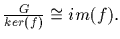
This is easy to see by identifying the image f(g) with the coset
gker(f). The map is a well defined isomorphism.
[In other words, we
identify
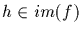 with its inverse image
with its inverse image
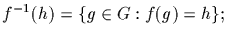 the
latter is simply gker(f), where f(g)=h. In the case of nonlinear
maps the preimage f-1(h) is usually called the level surface
corresponding to h.]
the
latter is simply gker(f), where f(g)=h. In the case of nonlinear
maps the preimage f-1(h) is usually called the level surface
corresponding to h.]
The first isomorphism theorem tells us that the factor groups of G
over its various normal subgroups are, up to isomorphism, precisely
the homomorphic images of G.
2. If 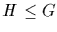 and
and 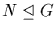 , then
, then
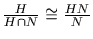 .
.
To see this, consider the restriction to H of the natural homomorphism
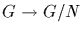 .
Its kernel is
.
Its kernel is 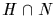 .
Its image consists of all cosets
of N having representatives in H, which is precisely the group
(HN)/N. The first isomorphism theorem allows us now to conclude
that
.
Its image consists of all cosets
of N having representatives in H, which is precisely the group
(HN)/N. The first isomorphism theorem allows us now to conclude
that
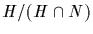 is isomorphic to (HN)/N.
is isomorphic to (HN)/N.
3. If
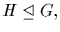
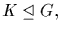 and
and 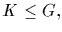 then
then
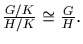
Define
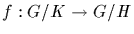 by f(xK)=xH. This is a well defined
homomorphism whose kernel is H/K and whose image is G/H.
The result follows now from the first isomorphism theorem.
by f(xK)=xH. This is a well defined
homomorphism whose kernel is H/K and whose image is G/H.
The result follows now from the first isomorphism theorem.
4. If 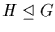 , then the map
, then the map
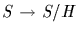 is a bijection between the set of
all subgroups containing H and the set of all subgroups of G/H.
Normal subgroups correspond to normal subgroups under this
bijection.
is a bijection between the set of
all subgroups containing H and the set of all subgroups of G/H.
Normal subgroups correspond to normal subgroups under this
bijection.
This is an important theorem that is self evident. The statement on
normality follows from the third isomorphism theorem.



Next: Group actions
Up: No Title
Previous: Definitions and notation
Gregory Constantine
1998-09-01