


Next: The Frobenius-Cauchy lemma
Up: No Title
Previous: Group actions
Denote by Sn the set of all permutations on a set with n elements,
which we take without loss to be
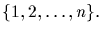 Under the composition of
permutations Sn is a group, called the Symmetric group of degree n.
Under the composition of
permutations Sn is a group, called the Symmetric group of degree n.
Let Sn act on the set of polynomials with integral coefficients;
specifically, 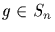 sends
sends
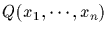 to
to
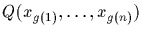 .
The orbit
of
.
The orbit
of
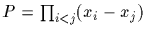 under this action is clearly
under this action is clearly
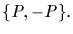 Thus the
stabilizer of P in Sn is a subgroup of index 2; call it An. Note that
the transposition (ij) sends P to -P, for all
Thus the
stabilizer of P in Sn is a subgroup of index 2; call it An. Note that
the transposition (ij) sends P to -P, for all 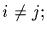 all transpositions
lie therefore outside An.
all transpositions
lie therefore outside An.
Represent Sn on the left cosets of An by left translation. Denote the
cosets by
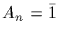 and
and
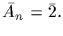 The kernel of this representation is
The kernel of this representation is
We conclude that An is normal in Sn. To summarize, this
representation sends 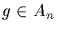 into
into
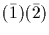 and
and
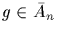 into
into
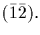
If
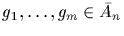 ,
then
,
then
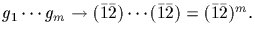 Clearly
Clearly
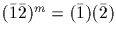 if and only if m is even. Thus
if and only if m is even. Thus
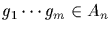 if and only if m is even.
A cycle
if and only if m is even.
A cycle
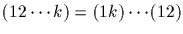 decomposes into k-1 transpositions.
Therefore a cycle of length k is in An if and only if k is odd. By
the decomposition into disjoint cycles of any element of S_
n we
conclude as follows:
decomposes into k-1 transpositions.
Therefore a cycle of length k is in An if and only if k is odd. By
the decomposition into disjoint cycles of any element of S_
n we
conclude as follows:
* A permutation belong to An if and only if it has an even number of cycles of
even length.
Elements of An are called even permutations. Elements of
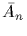 are
called odd permutations. We call An the
alternat
ing group of degree
n.
are
called odd permutations. We call An the
alternat
ing group of degree
n.
A group is simple if it has no normal subgroups other that itself and
1.
Theorem (Simplicity of
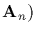 The alternating group of degree n is simple;
The alternating group of degree n is simple; 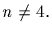
Proof: The group A3 is easily seen to be simple. When n=4 we have the
normal subgroup 1, (12)(34), (13)(24), (14)(23) in A4, so A4 is not
simple. Assume 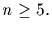
Step 1 An is generated by the 3-cycles. [In fact An is generated by
the n-2 3-cycles
![$\{ (12k):k\geq 3\}.]$](img136.gif)
Indeed, any element of An is a product of transpositions of the form
(ab)(cd) or (ab)(ac). Since
(ab)(cd)=(acb)
(acd) and
(ab)(ac)=(acb) we
conclude that An is generated by the 3-cycles. Furthermore,
(1a2)=(12a)-1,
(1ab)=(12b)(12a)-1,
(2ab)=(12b)-
1(12a), and
(abc)=(12a)-1(12c)(12b)-1(12a), which shows that every 3-cycle is
generated by a cycle of the form (12k).
Step 2 If H is a normal subgroup of An and H contains a 3-cycle,
then H=An.
Without loss
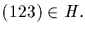 Then
Then
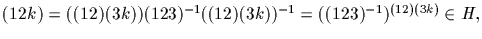 by normality.
Thus
An=<(12k): all
by normality.
Thus
An=<(12k): all
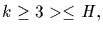 and H=An.
and H=An.
We now assume that 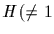 )
is normal in An. The idea is to show
that H contains a 3-cycle, necessarily. We then invoke Step 2 to
conclude the proof. Consider the exhausting possibilities examined
below.
)
is normal in An. The idea is to show
that H contains a 3-cycle, necessarily. We then invoke Step 2 to
conclude the proof. Consider the exhausting possibilities examined
below.
Case 1. Without loss assume that H contains
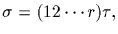 where
where
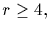 and
and 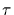 is disjoint of
is disjoint of
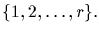 Then, by the normality of H,
H contains
Then, by the normality of H,
H contains
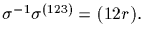 We are done by Step 2.
We are done by Step 2.
Case 2. Assume without loss that
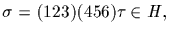 where
where 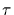 is a
product of disjoint transpositions. Then H contains
is a
product of disjoint transpositions. Then H contains
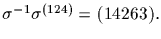 We are done by Step 1.
We are done by Step 1.
Case 3. Assume without loss that
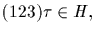 with
with 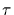 a product of
disjoint transpositions. Then H contains
a product of
disjoint transpositions. Then H contains
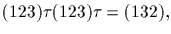 and we
are done by Step 2.
and we
are done by Step 2.
Case 4. Assume that H contains elements that are products of disjoint
transpositions. Without loss let
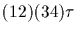 be such an element of H.
Then
be such an element of H.
Then
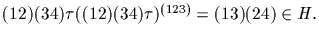 Since
Since 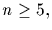 consider
consider
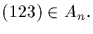 By normality H contains
(13)(24)((13)(24
))(135)=(135), and
we are done by Step 2. This ends the proof.
By normality H contains
(13)(24)((13)(24
))(135)=(135), and
we are done by Step 2. This ends the proof.



Next: The Frobenius-Cauchy lemma
Up: No Title
Previous: Group actions
Gregory Constantine
1998-09-01