


Next: Sylow's theorems
Up: No Title
Previous: Simplicity of the Alternating
Let V and W be sets, and S a subset of the Cartesian product
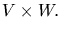 If
If
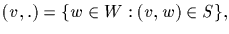
and
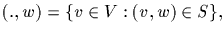
then it is self evident that
[Indeed, we are merely expressing the cardinality of S in two
different ways. First by fixing the first coordinate and
summing over the second, then by initially fixing the second and
summing over the first.] We call this two way counting.
Often the region S is rectangular, in which case we have
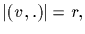 for all
for all 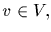 and
and
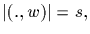 for all
for all 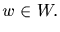 Then
Then
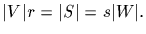
Let the group G act on a set S. Denote by
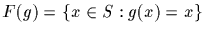 the
set of points in S fixed by the group element g. Denote by t the
number of orbits of G on S.
the
set of points in S fixed by the group element g. Denote by t the
number of orbits of G on S.
The Frobenius-Cauchy Lemma
The number of orbits of G on S is equal to the average number of
points left fixed by the elements of G.
[In symbols,
![$t={1\over {\vert G\vert}}\sum_{g\in G}\vert F(
g)\vert .]$](img164.gif)
Proof: We count in two ways the cardinality of the set of pairs
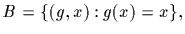 with g in G and x in S. Observe that in this case
(g,.) is simply F(g), and (.,x) is Gx, the stabilizer of x in G.
Therefore,
with g in G and x in S. Observe that in this case
(g,.) is simply F(g), and (.,x) is Gx, the stabilizer of x in G.
Therefore,
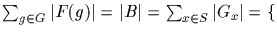
upon sorting by orbits
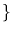
Here the xi's are representatives from distinct orbits. This ends the
proof.
Theorem (Cayley)
Every group can be faithfully represented as a regular permutation
group.
Proof: Let
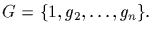 Consider the square array of
n2 letters (elements of G) formed as follows:
Consider the square array of
n2 letters (elements of G) formed as follows:
1
g2 g3 g4  gn
gn
g2 g22 g3g2 g4g2  gng2
gng2
gn g2gn g3gn g4gn  gn2
gn2
If we consider the permuatations by way of which each row in this
array is obtained from the first, we obtain a permuatation group on
n letters. Each permutation besides the identity involves all of the
n letters (i. e., it has no fixed points). The representation is
faithful since no two of the resulting permutations are the same.
Furthermore, each letter of G is replaced once and only once by
every other letter. The resulting permutation group is transitive
and regular. End of proof.
In a similar manner one can act with the group G, by multiplication
on the left, on the left cosets of a subgroup H of G. Let the set of
cosets be
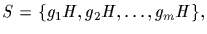 where where g1=1
and
where where g1=1
and
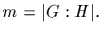 An element
An element 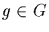 is
represented as
is
represented as
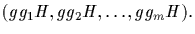 The kernel of this representation
consists of
The kernel of this representation
consists of 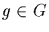 such that
ggiH=giH, for all i. In particular
gg1H=g1H, or gH=H, which shows that the kernel is in H. Generally such a
representation is not faithful. It becomes faithful,
however, if the only normal
subgroup of G contained in H is 1, since in that case the kernel of the
representation must necessarily be 1.
such that
ggiH=giH, for all i. In particular
gg1H=g1H, or gH=H, which shows that the kernel is in H. Generally such a
representation is not faithful. It becomes faithful,
however, if the only normal
subgroup of G contained in H is 1, since in that case the kernel of the
representation must necessarily be 1.



Next: Sylow's theorems
Up: No Title
Previous: Simplicity of the Alternating
Gregory Constantine
1998-09-01