


Next: Elements of a given
Up: No Title
Previous: The Frobenius-Cauchy lemma
A group of order pn, with p a prime number, is called a p-group.
We shall examine actions of p-groups on various sets.
Let H be a p-group acting on a set S. Since the length of an orbit
divides the order of the group, which is a power of p, it
follows that the length of an orbit is either 1 or is divisible by p.
Let
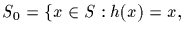 for all
for all 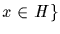 be the set of
orbits of length 1. The lengths of the orbits in S but not in S0 are
all divisible by p; their cardinalities are proper powers of p.
We thus conclude as follows:
be the set of
orbits of length 1. The lengths of the orbits in S but not in S0 are
all divisible by p; their cardinalities are proper powers of p.
We thus conclude as follows:
The mod p lemma (MPL)
If a p-group acts on S, then
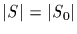 (mod p).
(mod p).
Theorem (Cauchy)
If a prime p divides the order of a group, then the group contains
elements of order p.
Proof: Denote the group by G. Let
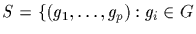 and
and
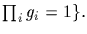 Since exactly p-1 elements can be freely selected from G
into an n-tuple
Since exactly p-1 elements can be freely selected from G
into an n-tuple
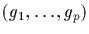 ,
and the remaining element is uniquely determined as the inverse of
the product of the elements already selected, it follows that the
cardinality of S is
,
and the remaining element is uniquely determined as the inverse of
the product of the elements already selected, it follows that the
cardinality of S is
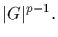 Let the cyclic group of order p, Zp, act
on S by cyclic shifts, specifically as follows:
Let the cyclic group of order p, Zp, act
on S by cyclic shifts, specifically as follows:
(Use the fact that gh=1 implies hg=1, to verify that this is indeed
a group action.)
In this case
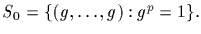 Clearly S0 is nonempty, since
Clearly S0 is nonempty, since
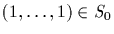 .
On the other hand, the MPL informs us that
.
On the other hand, the MPL informs us that
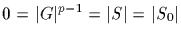
(mod
p),
since p divides
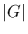 ,
by assumption . We thus conclude that
,
by assumption . We thus conclude that
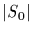 is
divisible by p.
This shows that there exist elements of order p in G. End of proof.
is
divisible by p.
This shows that there exist elements of order p in G. End of proof.
We write (a,b)=1 if integers a and b are relatively prime, that is,
when they share no common primes in their prime factorizations.
A
Sylow
p-subgroup of G is a p-subgroup of G maximal with respect
to inclusion on the p-subgroups of G.
Theorem (Sylow)
(a) If G is a group of order pnm, with p prime, 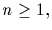 and (p,m)=1,
then G contains a subgroup of order pi for each
and (p,m)=1,
then G contains a subgroup of order pi for each
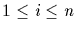 and every
subgroup of G of order pi,
and every
subgroup of G of order pi,
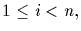 is normal in some subgroup of
order pi+1. In particular, Sylow p-subgroups exist.
is normal in some subgroup of
order pi+1. In particular, Sylow p-subgroups exist.
(b) If H is a p-subgroup of G, and P is any Sylow p
-subgroup of G,
then
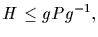 for some
for some 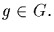 In particular, any two Sylow
p-subgroups are conjugate in G.
In particular, any two Sylow
p-subgroups are conjugate in G.
(c) The number of Sylow p-subgroups of G divides the order of G and
is equal to 1 modulo p.
Proof:
(a) We proceed by induction on i. Since p divides
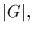 elements of
order p exist in G by Cauchy's theorem; such an element generates a
subgroup of order p. Assume that H is a subgroup of order pi,
elements of
order p exist in G by Cauchy's theorem; such an element generates a
subgroup of order p. Assume that H is a subgroup of order pi,
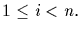 Then p divides
Then p divides
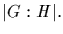 Let S be the set of right cosets of H
in G. Act with H on S by left translation, that is
h
(gH)=(hg)H.
Then S0 consists of cosets left fixed by H. Coset gH in in S0 if
and only if hgH=gH for all
Let S be the set of right cosets of H
in G. Act with H on S by left translation, that is
h
(gH)=(hg)H.
Then S0 consists of cosets left fixed by H. Coset gH in in S0 if
and only if hgH=gH for all 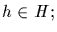 this happens if and only if
this happens if and only if
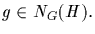 We thus conclude that S0 consists of exactly those
cosets of H that are in NG(H). By the MPL
We thus conclude that S0 consists of exactly those
cosets of H that are in NG(H). By the MPL
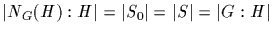 (mod p). Since
(mod p). Since
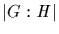 is divisible by p,
we conclude that p divides
is divisible by p,
we conclude that p divides
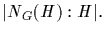 By Cauchy's theorem there is a
subgroup
By Cauchy's theorem there is a
subgroup 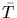 of order p in NG(H)/H. We are therefore assured the
existence of a subgroup T in NG(H),
of order p in NG(H)/H. We are therefore assured the
existence of a subgroup T in NG(H),
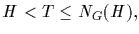 such that
such that
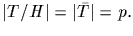 The order of T is clearly
The order of T is clearly
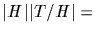 pip=pi+1. Since
pip=pi+1. Since
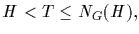 H is normal in T.
H is normal in T.
(b) Let S be the set of right cosets of P in G. Act with H on S by
left translation. Clearly
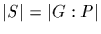 ,
and p does not divide
,
and p does not divide
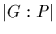 since
P is a Sylow p-subgroup. By the MPL
since
P is a Sylow p-subgroup. By the MPL
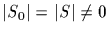 (mod p), and S0 is,
therefore, nonempty. There exists a coset gP in S0.
(mod p), and S0 is,
therefore, nonempty. There exists a coset gP in S0.
If H is a Sylow p-subgroup we necessarily have
H=gPg-
1.
(c) Let S be the set of all Sylow p-subgroups of G.
By part (b) we know that if G acts by conjugation on S,
the action is transitive, that is, there is one orbit only.
The number of Sylow p-subgroups is the length of the orbit, which in
turn divides the order of G.
Let P be a Sylow p-subgroup of G. Act with P on S by conjugation.
As Sylow p-subgroups of NG(Q), P and Q are conjugate in NG(Q).
But Q is normal in NG(Q) and therefore P=Q. Thus
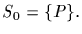 By MPL
By MPL
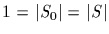 (mod p). This end the proof.
(mod p). This end the proof.



Next: Elements of a given
Up: No Title
Previous: The Frobenius-Cauchy lemma
Gregory Constantine
1998-09-01