
Back to course document list.
Interpretive Assignments
500 words
1. Lorentz Transformation of Special Relativity
(Easier)
In Ch.XI of Einstein's popular text, Relativity: The Special and the General Theory, Einstein shows that the light postulate is respected by the Lorentz transformation. A light signal moves according to x=ct. He transforms it to a new inertial frame of reference in which it turns out also be described by x'=ct'. (See the chapter for notation.)
(a) How does this vindicate the light postulate?
(b) Redo Einstein's calculation for the case of x = -
ct. (Note the "minus.")
(c) Show that a corresponding calculation for the Galilean transformation
(specified on p. 40.) fails.
OR
(Harder)
At the bottom on one of the pages of Section 3 of Einstein's special relativity paper of Einstein remarks on a simpler derivation of the Lorentz transformation

Reconstruct Einstein's derivation.
To make life a little easier, consider only the transformation that takes (t, x) to (τ, ξ). Note also that Einstein's condition is only strong enough to recover the Lorentz transformation with the arbitrary factor φ(v).
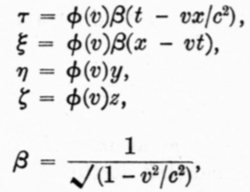
Hints: Follow these steps.
I. Assume the transformation is linear and write it in the general form
τ = φ(v)(t + bx) ξ =
ψ(x-vt)
II. Substitute these equations into ξ2 = c2 τ2
III. For this equation to reduce to x2 = c2 t2, the "xt" terms must vanish, which puts a significant constraint on the constants in the transformation equations.
IV. Keep working the algebra until you have arrived at x2 = c2 t2. You should find that the condition needed to achieve this amounts to the Lorentz transformation for the simpler case of (t, x) to (τ, ξ).
2. Principle and Constructive Theories OR E = mc2
(Critical-analytic)
Einstein's pathway to his special theory of relativity included him making use of a distinction between what he called "principle theories" and "constructive theories." The distinction is described in a 1919 article written for The Times (London), "What is the Theory of Relativity?" He also recounts the role the distinction played in his discovery of special relativity in a paragraph in his Autobiographical Notes.
(a) What is the distinction Einstein draws?
(b) How did it play a role in his thinking concerning the discovery of
special relativity?
(c) Aside from Einstein's examples, can you find an example of a principle
theory and a constructive theory? Which are they? Why are they properly
categorized so?
(d) Einstein claimed certain advantages for each type of theory in his
1919 article. Do these benefits arise in your examples? Explain.
Since this assignment requires a simple text answer, please do not handwrite it. Please type it and hand in a printed version.
OR
(mathematical, easier)
In 1946, Einstein gave "An Elementary Derivation of the Equivalence of Mass and Energy," published in his Out of My Later Years.
(a) Reconstruct the derivation.
(b) Einstein says his derivation uses the expression for the aberration of
starlight from astronomy. How is it possible to use this expression when
there are no stars talked of in the derivation?
(c) There is a typo in the derivation associated with the effect of
aberration. What is it?
(d) How does this derivation differ from the original derivation of 1905?
(e) Is it improved? How?
OR
(mathematical, harder, but I think it is easy once you see how to set it up)
In Section 1 of A. Einstein, "The Principle of Conservation of Motion of the Center of Gravity and the Inertia of Energy," (1906) Doc. 35 in Einstein Papers, Vol 2, Einstein presents a "special case" thought experiment in which he uses the conservation of the motion of the center of gravity to arrive at the inertia of energy. The thought experiment analyses a cyclic process involving very small quantities of mass and very small dislocations in space. The computation requires the selective neglecting of certain small quantities.
The basic idea of the thought experiment can be shown without using very small quantities if they are replaced by differential operators. To do this, consider a mass m that emits radiation at a steady rate s in a fixed direction. Compute the center of mass of the total system, assuming that the radiant energy emitted has inertial mass. The position of this center of mass must remain fixed. That is, its time derivative must vanish.
Use the condition of the vanishing of this time derivative at the moment of first emission of the radiation to recover the inertia of energy.
OR
(mathematical, harder, but satisfying if you can crack it!)
In Section 2 and later of A. Einstein, "The Principle of Conservation of Motion of the Center of Gravity and the Inertia of Energy," (1906) Doc. 35 in Einstein Papers, Vol 2, Einstein provides another demonstration of the inertial of energy this time using a result pertaining to the center of gravity. The proof is given in terms of field components. That is "X, Y, Z" instead of the electric field vector E.
Convert Einstein's analysis into the now standard vector notation using "div, grad, curl" etc. What precisely is the result shown?
NB.The editorial notes to the German text in Einstein Papers, Vol.2, contains corrections to typographical errors in the text. And, of course, Einstein's "V" is now our "c."
3. Orthogonal Transformations
In the opening pages of Einstein's text on relativity theory, Meaning of Relativity, Einstein introduces what are now called "orthogonal transformations." They are the analog in ordinary three dimensional Euclidean space of the Lorentz transformation in Minkowski spacetime. They are defined as the transformation of the three Cartesian coordinates (x, y, z) = (x1, x2, x3) that preserves the Euclidean line element
(Δs)2 = (Δx1)2 + (Δx2)2 + (Δx3)2 = Σν=1,2,3(Δxν)2
That is, we transform to new coordinates (x', y', z') = (x'1, x'2, x'3) such that
Σν=1,2,3(Δxν)2 = Σν=1,2,3(Δx'ν)2 (*)
Einstein shows that the transformations that preserve this Euclidean line element are given by his equation (3) on p. 7:
x'ν= aν + Σα=1,2,3 bναx'α (3)
where bνα are constants that satisfy the orthogonality condition
Σν=1,2,3 bναbνβ = δαβ (4)
(a) Show that a translation
x'ν= aν + xν
where aν = (a1, a2, a3) are three constants, is an orthogonal transformation that satisfies (4).
(b) A rotation by an angle theta around the x3 = z axis is given by bνα's that satisfy
Show that this transformation is an orthogonal transformation that
satisfies (4).
(c) Use (3) and (4) to prove that an orthogonal transformation leaves the Euclidean interval invariant; that is, orthogonal transformations satisfy (*).
(d) (Optional) On p.7, Einstein uses a power series expansion to establish that an orthogonal transformation from xν to x'ν must be linear. Supply the missing steps in his argument. (NB. This might be hard. I haven't been able to see how to answer this one.)
-------------------
Hint: If you know some matrix algebra, the three coordinates (x1, x2, x3) can be represented by a column vector x = (x1, x2, x3)T. The transformation (3) is then just
x' = a + b x
Einstein's orthogonality condition (4) can be represented as
bTb = I or, equivalently bT = b-1
Using this matrix representation simplifies the presentation of the answers.