

http://commons.wikimedia.org/wiki/File:2010-07-20_Black_windup_alarm_clock_face.jpg http://commons.wikimedia.org/wiki/File:Old_Pendulum_clock.jpg
| HPS 0410 | Einstein for Everyone |
Back to main course page
Special Theory of Relativity: Clocks and Rods
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Einstein based his special theory of relativity on two postulates, the principle
of relativity and the light postulate. If we adopt these two
principles, we already know that things cannot remain as they have been in
classical Newtonian physics. Imagine a light signal flying past us; and an
inertially moving spaceship that speeds after it. An immediate consequence
of the light postulate is that observers in the inertially moving
spaceship will not judge the light signal to have slowed, no matter how
fast they are moving past us. That is impossible according to classical
Newtonian physics.
If we are to retain both of Einstein's postulates, we will
have to make systematic changes throughout our
physics. Let us begin investigating these changes. They will
overturn our classical presumptions about space and time.
The first change we will investigate has to do with time. An inertially moving clock runs more slowly than one at rest.


http://commons.wikimedia.org/wiki/File:2010-07-20_Black_windup_alarm_clock_face.jpg
http://commons.wikimedia.org/wiki/File:Old_Pendulum_clock.jpg
| To see how this comes about, we could undertake a
detailed analysis of a real clock, like a wristwatch, a pendulum
clock or a mechanical wind-up clock. That would be difficult and
complicated--and unnecessarily so. All we need is to demonstrate the
effect for just one clock and that will be enough, as we shall see
shortly, to give it to us for all clocks. So let us pick the
simplest design of clock imaginable, one specifically
chosen to make our analysis easy. A light clock is an idealized clock that consists of a rod of length 186,000 miles with a mirror at each end. A light signal is reflected back and forth between the mirrors. Since light moves at 186,000 miles per second, the signal will require one second to traverse the length of the rod on its outward journey; and one second to make the return journey. That is, the signal requires two seconds for the round trip. The clock user is located at one end of the rod and records the successive returns of the light signal as the ticking of the clock. Thus the clock registers a tick for the user once every two seconds. |
| Why, you might ask, do we use the "round trip"
time of the light signal to define the ticks of the clock? Why
not take the ticks to be the arrivals of the light signal
at either end of the rod? Then the clock ticks once every second. The difficulty with this arrangement is that successive ticks of the light clock would be happening at different places. If one end of the rod is "near" the user and the other is "far" from the user, then the successive ticks would be: tick (near), tick (far), tick (near), tick (far), tick (near), tick (far),... In a non-relativistic world, distributing the ticks over different locations in space might be a nuisance. But it would trigger no foundational problems. Each distant tick would be associated with a definite moment at the other location. This is no longer the case in special relativity. If the ticks and other events are located in different places, complications in determining their time order will become a matter of central concern for us, in chapters to come. We avoid these problems by keeping the readings of of the clock localized to one position in space. |
Readers of earlier versions of this chapter will
notice that these earlier versions counted the ticks at either end
of the rod. I thank Balazs Gyenis for urging me to employ the localized ticking of the present version. |
| Here
are some light clocks ticking: |
Older, animated gif is here.
| You might imagine that the idea of a light clock
is so fanciful that one could never be constructed. Where can we
find a rod of length 186,000 miles? How could we arrange a light
signal to bounce back and forth along one? The curious fact,
however, is that something pretty close to a light clock has already
been built. Astronauts in the Apollo 11, 14 and 15 moon missions and
the unmanned Lunokhod 1 and 2 rovers placed reflectors
at various locations on the moon's surface. These are
corner reflectors, like reflectors on the rear of cars and bicycles.
They have the key property of reflecting a light signal directly
back to its source. Astronomers on earth fire a laser pulse through a telescope at one of the reflectors. They then measure the time for the laser pulse to return to earth. Since the average distance to the moon is 239,228 miles, the pulse takes about 2.5 seconds to return. This arrangement is almost exactly that of the light clocks described. The light clock's 186,000 mile rod is replaced by the 28% larger distance from the earth to the moon. |
The radar ranging experiments are not quite like the idealized light clocks of our thought experiments. The ends of our rod are at rest in an inertial frame of reference. There are, however, many slight movements in the earth-moon distance gauged in radar ranging. For example, the telescope on earth partakes in the daily rotation of the earth. The distance to the moon is not fixed but varies over the course of a month. |

Images: blue marble
https://eoimages.gsfc.nasa.gov/images/imagerecords/57000/57723/globe_west_2048.jpg
moon
https://commons.wikimedia.org/wiki/File:Lunar_retroreflector_locations.jpg
We use the light clocks in our thought experiments to gauge the rates of clocks, based on the known length of the clock's rod. The astronomers use the laser ranging experiments in the reversed way. They measure the timing of the ticks on earth and use that time to estimate the distance from the earth to the moon. These experiments have enabled extremely precise measurements of this distance.
What happens when a light clock is set into rapid motion, close to the speed of light? It is easy to see without doing any sums that the light clock will be slowed down. That is, it will be slowed down in the judgment of someone who does not move with the light clock.
First, we will take the simple case of a light clock whose motion is perpendicular to the rod. The light clock will function as before. But now there is an added complication. The light signal leaves one end of the rod and moves toward the other end. But since the rod is moving rapidly, the light signal must chase after the other end as it flees. As a result, the light signal requires more time to complete the round trip journey to the far end of the rod and back. That means that the moving light clock ticks more slowly than one at rest.
Remember the light postulate. It tells us that the light always travels at the same speed in any inertial frame of reference. That the rod along which it bounces is moving rapidly will not alter the speed of the light.
Here's an animation that shows a light clock at rest and a second light clock that moves perpendicular to its rod. The light signal in the moving clock chases after the rod. To reach the other end, it covers more distance and, as a result, requires more time.
Here are the older "gif" versions of the these animations,
| If you watch the animation carefully, you will see that the moving light clock ticks at exactly half the speed of the resting clock. That is because the light signal of the moving clock has to cover twice the distance to go from one end of the rod to the other. | To get this doubling of the distance takes a careful adjustment of the speed of the moving clock. It turns out that the moving clock has to be traveling at 86.6% the speed of light. |
Just how much slowing do we get for some particular speed? That question turns out to be easy to answer with a little geometry. The trick is to figure out how much distance the light signal has to travel to reach the other end of the rod. Once we know that distance, we know the time taken, since light always travels at 186,000 miles per second.
|
|
To make things interesting, let's take a very high speed: 99.5% the speed of light. (We'll write this compactly as "0.995c.") An observer traveling with the clock will still find that the light signal bounces backwards and forwards between the mirrors as before. |
This process unfolds quite differently from the perspective of an observer who stays behind and does not move with the clock. That second observer will find the light signal to depart one end of the light clock's rod and chase after the other end as it recedes rapidly at 0.995c. Once it finally manages to catch the other end of the rod and begin its return journey, it will once again be chasing after a rapidly receding rod end. The path traveled by the light signal will now be along a diagonal:
| This is a greatly elongated path. It is so because the analysis is carried out within the special theory of relativity. Light propagates in accord with the light postulate. That means that this signal must travel at c while it chases after a rod receding from it at 0.995c. | This figure is not drawn to scale. If it were to be, it would be stretched in its width to almost 20 times the height the of the figure and not fit on this screen. |
It follows that the light signal will take much more time to complete its trip to the end of the rod and back. That is, the light clock will tick much more slowly than a resting light clock. It turns out that the clock is slowed to one tenth is normal rate. That is, the light signal now takes ten second to complete the outward leg of its motion and and ten seconds to complete the return motion. The clock ticks not once each 2 seconds, but once each 20 seconds.
A little arithmetic lets us see that the clock is slowed
just this much. Over a period of ten seconds, the light clock moves
a distance:
10 x 0.995c = 10 x 0.995 x 186,000 miles
= 1,850,700 miles.
That means that path taken by the light on its outward journey is the
hypotenuse of a right angled triangle with sides 186,000 miles and
1,850,700 miles.
| Pythagoras' theorem tells us the
diagonal is 1,860,000 miles since 1,860,000 miles2 = 1,850,700 miles2 + 186,000 miles2 |
We can add the length of the hypotenuse to the figure to see the distance the light signal must travel on its outward and return journeys:
That observer at rest will agree with one that moves with the rod: a light signal leaves one end of the rod and arrives at the other end and then returns. But the observer at rest judges that the light signal must travel ten times the distance that it would have to cover if the clock were at rest. For the hypotenuse to be traversed is ten times the length of light clock's rod
1,860,000 = 10 x 186,000
This means that the signal will now take 10 seconds to reach the far end of the rod; and the same 10 seconds again to return to the near end. The ticks are now spaced 20 seconds apart.
Setting the arithmetic aside,
the result is simple. Since the light signal must travel so much farther
to traverse the rod of a moving clock, it takes much longer to do it.
Hence a moving light clock ticks slower. In this case, for a clock moving
at 99.5% the speed of light, it ticks once each twenty seconds instead of
once each two seconds.
All light clocks slow when they move rapidly. What about other clocks? You might be tempted to say that light clocks are exceptional. They slow because they depend on light; and we are learning that light does odd things. So why not just say that light clocks slow when they are set in motion and that shows that light clocks are not good clocks after all? Why not just say that other, real clocks are not slowed? It is tempting to say this, but it does not work.
| A simple application of the
principle of relativity shows that all clocks must be
slowed by motion, not just light clocks. We set a clock of any
construction next to a light clock at rest in an inertial
laboratory. We notice that they both tick at the same rate. That must remain true when we set the laboratory into a different state of inertial motion. But since the light clock has slowed with the motion, the other clock must also slow if it is to keep ticking at the same rate as the light clock. |
You might still be tempted to say that the other clock would not keep pace with the light clock. Instead, you might say, it would keep running at just the same speed as it did when at rest. But then you would have devised a device that detects absolute motion, in contradiction with the principle relativity. That device would pick out absolute rest as the only state of motion in which the two clocks run at the same rate. Whenever the light clock ran slower than the other clock, we would know we are moving absolutely and we could use the difference of rates to determine just how fast that motion is. This cannot be; the principle of relativity prohibits it.
At first this might seem too easy. How can the principle of relativity force this slowing on all possible clocks?! Recall that the principle of relativity restricts all physical laws. It says that none of them are allowed a notion of absolute rest in space. This requirement forces systematic adjustments in almost every branch of physics. These adjustments will have the overall effect of forcing every clock that we might construct to slow when it is set in motion. For example, a mechanical clock keeps time by counting the oscillations of a mass bouncing on the end of a spring. A digital watch keeps time by counting the electromagnetically induced oscillations of a crystal. The physics of all of these systems will be altered slightly by the principle of relativity and in a way that will slow these clocks by the same amount as a light clock.
Perhaps the most extreme example of a clock is a human metabolic system. I can use my pulse to check that the light clock is running roughly at one tick for each two seconds. That check must give the same result in every inertial frame of reference. Hence my metabolism must slow in concert with the slowing of the light clock. That it should do this is fully to be expected. My metabolism is governed by complex laws of biochemistry. These laws must also respect the principle of relativity. So these laws also will be adjusted in a way that ensures that our metabolic clocks slow by just the same amount as a light clock, when both move at the same speed.
The outcome is that observers who move with a clock will not discern its slowing. For the observer's metabolism is slowed exactly as much as the clock. This unobservability of the slowing is required by principle of relativity. For, as we just saw, if I use my pulse beat to measure the rate of a clock, I must get the same outcome for the experiment if it is repeated with me and the clock set into rapid, uniform motion.
So far, we have considered a light clock whose rod is perpendicular to the direction of its motion. If we now consider a light clock whose rod is oriented parallel to the direction of motion, we will end up concluding that its rod must shrink in the direction of its motion. To get this result, we proceed by reasoning just as we have before. Once again we have a light signal on a moving clock, chasing after an end of a rod that flees rapidly. We now add in the extra complication that the rod is parallel to the direction of motion of the clock. That extra complication will force us to conclude that the rod has shrunk.
Getting to this result uses no new ideas or methods. It is just more arithmetic and a little messier, so if you are not too bothered by details piling up, work through what follows. Or, if you are not so brave, you can skip to the end and just read the final result.
To get to the result, we need two steps:
1
Light clocks oriented perpendicular to one another run at the same
speed.
| |
Take the light clock considered above. Image a second, identical
light clock with its rod oriented perpendicular to the first rod.
They are both at rest in some inertial frame of reference. So, once
again the principle of relativity requires that both
clocks run at the same speed. We could just leave it at
that--an application of the earlier result. However it is reassuring
to go through it from scratch. To begin, we don't need the principle of relativity to see that the clocks at rest run at the same rate. They will run at the same rate simply because they are the same clocks oriented in different directions. That just follows from the isotropy of space. All directions in space are physically equivalent. So the orientation of the clock cannot affect its speed. |
| Now imagine that we take the entire system of the two clocks and set it into rapid motion at, say, 99.5% the speed of light or "0.995c", in the direction of one of the light clocks. |
| An observer moving with the two light clocks must find them to continue to run at the same rate. We now do need the principle of relativity to establish this. Our earlier isotropy argument does not work anymore, since the two directions of the clocks are intrinsically different. One is perpendicular to the direction of motion; the other is parallel to it. The principle of relativity requires that they run at the same rate. For, if they ran at different rates, the device would be an experiment that could detect absolute motion. | What if, contrary to the principle of relativity,
the clocks ran at different rates when set in motion together? How
would this give us a device that could detect absolute motion? If
this happened, we could detect absolute motion just by taking two
identical light clocks, oriented perpendicular to each other, and
checking if they ran at the same rate. If we found them running at
the same rate, we would have found that we are at rest absolutely.
If we find that they do not run at the same rate, we would have
found that we are moving absolutely. It this an experiment anyone would actually try to do? It turns out that this a description at the broadest level of one of the most famous experiments in physics, the Michelson Morley Experiment. We shall look at it in a later chapter. |
2
The rod oriented in the direction of motion must shrink.
We know from the earlier analysis that a light clock (indeed any clock) moving at 99.5% the speed of light is slowed, so that it ticks only once in twenty seconds. So now we know that the light clock oriented parallel to the direction of motion must tick once each twenty seconds. But that cannot happen if everything is just as we describe it. Imagine the outward journey of the light signal.
How do I get this? If you have to know, here are the details. Think about the interval of space between the light signal and the end of the rod. At one boundary is a light signal moving at c. At the other boundary is the end of the rod moving just slightly slower at 99.5%c. It follows that the distance between the two boundaries diminishes at 100%c - 99.5%c = 0.5%c, which is 930 miles per second. The distance is initially 186,000 miles, so it takes 186,000/930 = 200 seconds to shrink to zero. That is when the light signal arrives at the rod's end. |
The light signal has to go from one end to the
other of a 186,000 mile rod. The light moves at c, 186,000 miles per
second. But the rod is also moving in the same direction at 99.5%
the speed of light, 0.995c. So the light has to chase after a
rapidly fleeing end and will need much more than a second to catch
it. With a little arithmetic it turns out that the
light will need 200 seconds to make the forward trip. |
| But the light clock has to tick once every twenty
seconds! Something has gone badly wrong. What has gone wrong is our
assumption that the rod parallel to the direction of motion retains
its length. That is incorrect. That rod
actually shrinks to 10% of original length, so the moving
pair of clocks really looks more like this: (The contraction is not drawn to scale or it would be much harder to see.) |
Now the light signal has time to
complete its round trip traversal of the rod and keep the clock
ticking at once each twenty seconds as expected. The signal just has far
less distance to travel so now it can maintain the rate of ticking
expected.
There are more details in this last calculation that I don't want to bother you with. But since some of you will ask, here they are--but only for those who really want them.
Overall it will turn out that the light signal needs 20 seconds to complete the journey from the trailing end of the rod to the front and then back. That is what we expect for one "tick." The catch is that virtually all of the 20 seconds will be spent in the forward trip and virtually none of it in the rearward trip. This effect figures in the relativity of simultaneity which we will discuss at some length later.
If you want to see this for yourself you should redo the calculations. If you do, you'll need to undo my rounding off. The rod is not contracted exactly 10%--I rounded things off to keep life simple. It is 9.987%. The ticks are not exactly 20 seconds apart, but 20.025 seconds. The forward trip will take 19.9750 seconds. The rearward trip will take 0.05 seconds. They sum to give a total round trip of 20.025 seconds as expected.
Here are some simplified animations that might make it easier to see why the rod of the light clock oriented in the direction of motion must contract to the keep the two light clocks ticking at the same rate. The simplified animations are drawn for the case of light clocks moving at 0.866c or 86.6% the speed of light. In that case the rod oriented in the direction of motion must shrink to half its rest length.
Here are two light clocks oriented perpendicular to one another and at rest in our inertial frame of reference. They tick at the same rate.
We now set the light clocks in motion at 86.6% the speed of light. The light clock oriented transverse to the direction of motion slows to half its resting speed. If the rods of the two light clocks remain the same length, then the light clock oriented in the direction of motion cannot match the rate of ticking of the other light clock. Its light signal requires much more time to reach the leading edge of its rod.
The two clocks will tick at the same rate if the rod of the clock oriented in the direction of motion shrinks to half its resting length. (This half is the amount needed for the particular case illustrated of the clocks moving at 86.6% the speed of light.) With this shortening of the rod, the light signal of the clock oriented in the direction of motion has less distance to travel. It can now complete the round trip along the length of its rod in the same time as does the light signal on the other clock. The two clocks are ticking at the same rate, as the principle of relativity requires. (Once again, the light signal of the clock oriented in the direction of motion spends almost all its time propagating in the forward direction and almost none in the returne direction.)
There is a loophole in the analysis, as presented so far. The rod of the light clock oriented in the direction of motion can be unchanged in length. Instead, we extend the length of the rod of the light clock oriented perpendicular to the direction of motion. We can increase this rod's length and thereby slow its clock's ticking enough, so that the two clocks tick at the same rate.
Nothing said so far precludes this variant way of keeping the two light clocks ticking at the same rate. It fails, however, if we try to develop the theory further. We will be unable to preserve the principle of relativity. To see why, imagine two light clocks in relative inertial motion, with their rods oriented perpendicular to the common direction of relative motion. Observers on one clock must then judge the other clock's rod to be extended. The principle of relativity requires that the same is true for judgments made by observers on the other clock concerning the first clock. However, they both cannot judge the other's rod to be extended. If the first judges the second's rod to be extended, the second must judge the first's to be contracted. The requirement of the principle of relativity is violated.
Is there a similar violation of the principle of relativity arising with the original result that rods in the direction of relative motion are contracted? Can observers in relative inertial motion in this case each judge the other's rods to be contracted, as the principle of relativity requires? It turns out that they can. To see why, however, requires an understanding of the relativity of simultaneity, which will be developed in the following chapters. In brief, the relativity of simultaneity applies to events separated spatially in the direction of relative motion. It protects the principle of relativity only if we assume that rods oriented in the direction of motion are contracted. It provides no protection for the variant case considered as a loophole.
The analysis is now complete. A light clock oriented perpendicular to the direction of its motion slows by a factor of 10 when it moves at 99.5% the speed of light. A light clock oriented parallel to the direction of its motion must slow by the same amount when it moves at 99.5% the speed of light. It can do this if its rod shrinks in the direction of motion by a factor of ten.
This length contraction result is quite general. Any object--such as a spaceship placed next to the rod--must also contract by same amount. If it did not, then we could use the difference in the contraction of the light clock rod and the object to reveal our absolute motion. We would have an absolute motion detector. But that is prohibited by the principle of relativity.
The effect is different in different directions: the object is shortened in the direction of its motion, but its size remains the same in a direction perpendicular to its motion. That is, the shapes of moving bodies are distorted from their resting shapes. Here is how that that distortion goes:
Spaceship at rest:
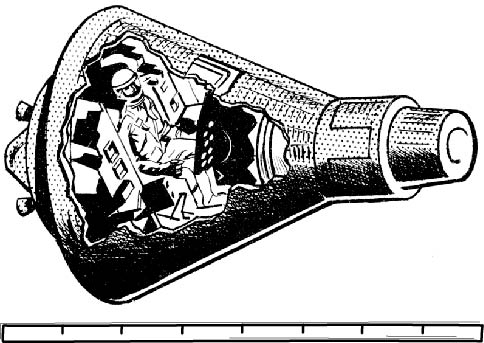
Spaceship moving rapidly:
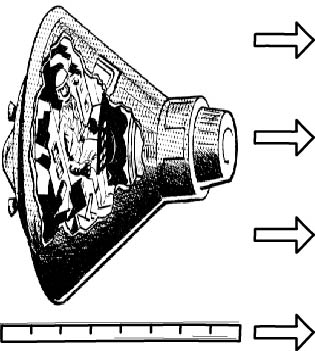
Spaceship moving even more rapidly:
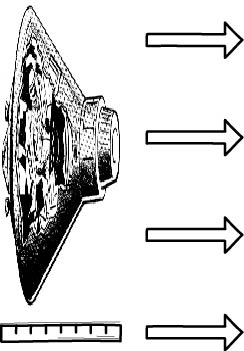
http://upload.wikimedia.org/wikipedia/commons/6/67/Spacecraft_%28PSF%29.png
The length contraction effect applies not just to ordinary mechanical objects like spaceships. It applies to living beings as well. When anything at all is set into motion, it contracts in the direction of its length.
A human at rest:
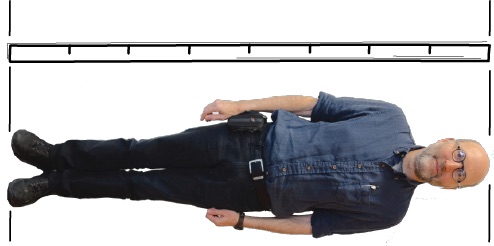
A human in rapid motion:
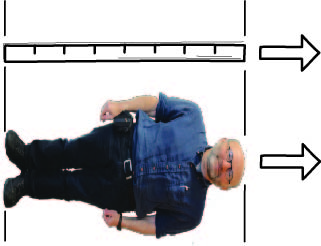
The principle of relativity assures us that, when we move, we have no direct awareness of this relativistic contraction effect. When we are at rest, every experiment can do would show us that we have our normal size. If I measure my height with a measuring rod, I will get the expected result. If I am now transported to a spaceship moving at 99.5% the speed of light, the experiments must come out the same. The principle of relativity requires it. This will be so, even though people back on earth would judge me to have shrunk by a factor of ten in the direction of my motion. And since I judge them to moving in the opposite direction, I would judge them to have shrunk correspondingly, while they have no measurement that can reveal it!
The analysis given above using light clocks is one of the simplest ways of arriving at the two effects of clock slowing and length contraction. The idea of a light clock, however, is not contained in Einstein's 1905 paper on the special theory of relativity. It is an interesting exercise to track down how the idea first came into the relativity literature.
Tracking it down is not so straightforward. The idea of tracking a light signal on its outward and return journal is already in Einstein's 1905 paper. He uses it in his procedure for synchronizing clocks and then in his derivation of the theory's basic equations ("Lorentz transformations"). Tracking reflected light signals is such a natural operation in relativistic analyses that it turns up everywhere. Einstein and many others who examine it do not identify the procedure as a "light clock."
We come a little closer to the idea of a light clock in Lewis and Tolman's early 1909 recounting of relativity theory. They gave an analysis of clock slowing and rod contraction that is very similar to the one in this chapter (and they had it first!). A figure from one page of the analysis is shown here, with my arrows superimposed to show the light paths. The light paths along the line "o-p" correspond to those of the light clock at rest, with the clock perpendicular to the direction of motion. The light paths along the lines "m-n-m'" corresponds to those of the light clock in motion, with the light clock again perpendicular to the direction of motion.
 |
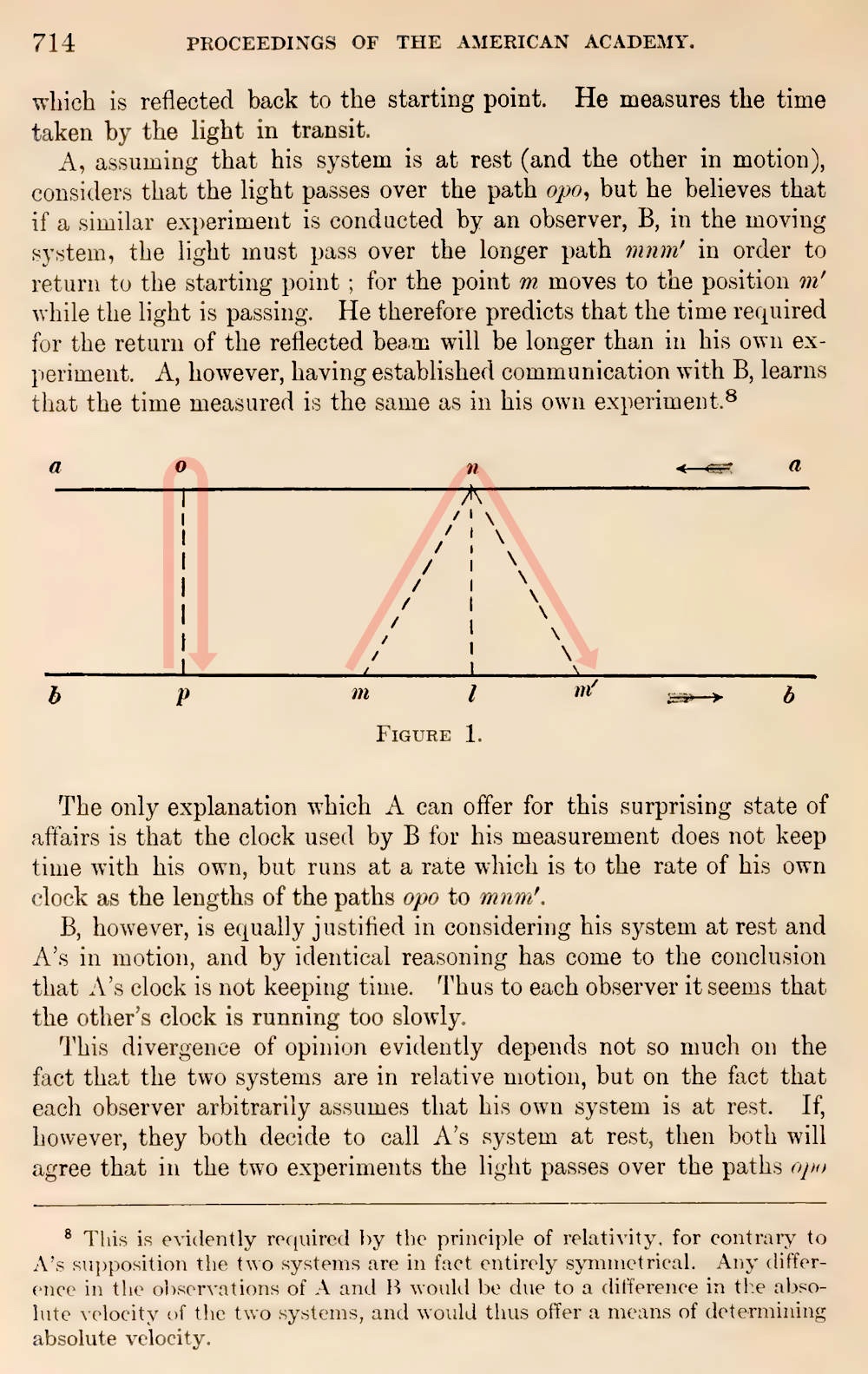 |
The earliest explicit identification I could find in Einstein's work of the use of reflected light signal as a clock is in a 1912 paper on gravity. He does not use the light clock to discern effects within special relativity. Instead it is used to discern temporal effects due to gravity in a theory that is a precursor to general relativity.
It is in his paper Albert Einstein, "Lichtgeschwindigkeit and Statik des Gravitationsfeldes," [The speed of light and static gravitational fields] Annalen der Physik 38 (1912), pp. 355-69.


Einstein says:
"Here [in regions of different gravity] we can use something like two mirrors at a distance of 1 cm as a clock by counting the number of times a light signal goes back and forth;..."
"Als Uhr können wir uns dabei etwa zweier Spiegel von der Distanz 1 cm bedienen, indem wir die Zahl der Hin- und Hergänge eines Lichtsignals zählen; ..."
The earliest identification I could find of the construction as a "light clock" by name is in Birkhoff's 1924 analysis. He uses the light clock in essentially the same way as is done in this chapter. That is, he argues that a light clock and other well-constructed clocks must run at the same rate.



Over the last couple of decades, a light clock is sometimes referred to as an "Einstein-Langevin clock." I have been unable to locate work by the French physicist Paul Langevin that would justify the name. I did find a 1911 work that replicates the Lewis and Tolman analysis of 1909.
Paul Langevin, "Le Temps, l’Espace et la Causalité dans la physique moderne," Bull. Soc. franc. Phil. Séance de 19 Oct., 1911, 1-46.
As with Lewis and Tolman, the expression "light clock" is not used. The origin, or at least an early mention of this name "Einstein-Langevin clock" is in the work of the French physicist Henri Arzeliès, well after the time of Birkhoff's usage.
Henri Arzeliès, Relativistic kinematics. Oxford, New York, Pergamon Press, 1966. The work is an English translation of texts written in French in the 1950s.
Page 21 has the first of several mentions of "Einstein-Langevin clock."
Calling it an "Einstein clock" is strained, since the notion appeared so incidentally in Einstein's writing and in a context different from special relativity. The addition of Langevin to the name would also appear to be strained, unless we can find a more secure source in Langevin's writing.
We have learned that a clock
moving at 99.5% the speed of light, slows by a factor of ten. It ticks
once each twenty seconds instead of once each two seconds. A
rod, oriented in the direction of motion, shrinks to 10% of its
length. Rods perpendicular to the direction of motion are unaffected.
These two effects have always been there. They were not
noticed until Einstein's time because they are so very, very small as long
as our speeds are far from that of light. They become marked when we get close
to the speed of light. The closer we get the the speed of light,
the closer clocks come to stopping completely and rods come to shrinking
to no length in the direction of motion. For more details of how the
effects depend on speed, see What
Happens at High Speeds.
Finally, you might imagine that a direct experimental test
of the slowing of clocks is impractical. How are we going to accelerate a
clock to a speed close to that of light and then take readings from it? It
turns out, however, that nature provides us something close enough to
count as a test. Muons, moving at close to the speed
of light, are created by cosmic rays that smash into our
atmosphere. Muons are highly unstable and should never survive long enough
to make it to the earth's surface, where we can detect them. Yet they do
survive because their internal clocks are greatly slowed by their high
speed, so they persist much longer than they would without that high
speed. For more see:
Cosmic
Rays: Evidence for special relativity happening all the time