Back to main course page

Special Theory of Relativity

Relativity of Simultaneity

John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh

When Einstein first hit upon special relativity, he thought one effect of special importance, so much so that it fills the first section of his "On the Electrodynamics of Moving Bodies." It is the relativity of simultaneity. According to it, inertial observers in relative motion disagree on the timing of events at different places. If one observer thinks that two events are simultaneous, another might not. At first this will seem like just another of the many novel effects relativity brings. However, as we explore more deeply, you will see that this is the central adjustment Einstein made to our understanding of space and time in special relativity . Once you grasp it, everything else makes sense. (And until you do, nothing quite makes sense!)

Here are the first two pages of Einstein's "On the Electrodynamics of Moving Bodies." The first section, "Definition of Simultaneity," establishes the relativity of simultaneity. It was the first step in developing the special theory of relativity.

 In 1917, Einstein wrote a popular account of relativity theory. Once again, the first step in developing the results of the special theory of relativity was to establish the relativity of simultaneity. Here is the table of contents of an English translation.  

Using Light Signals to Judge the Time Order of Events

There is a quick way to see how this comes about. Imagine a long platform with an observer located at its midpoint. At either end, at the places marked A and B, there are two momentary flashes of light. The light propagates from these events to the observer. Let us imagine that they arrive at the same moment, as they do in the animation below. Noticing that they arrive at the same moment and that they come from places equal distances away, the observer will decide that the two events happened simultaneous.

Another outcome is closely related. Imagine also that there are clocks located at A and B. If both clocks show the same reading at the events of the two flashes, then we would judge the two clocks to be properly synchronized. That is what the platform observer judges since, as the animation shows, both clocks read "0" when the flashes occur at each location.

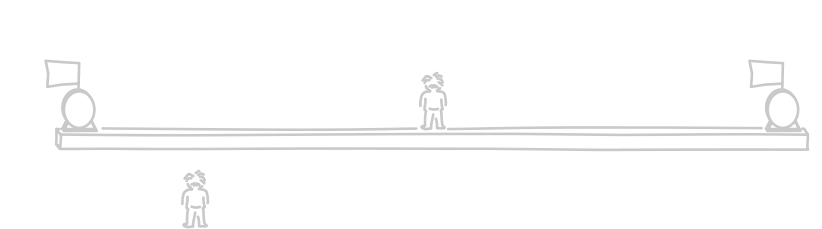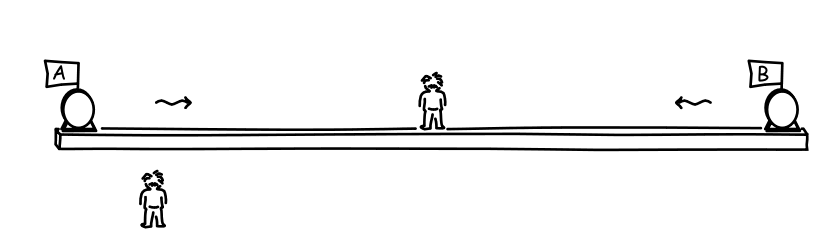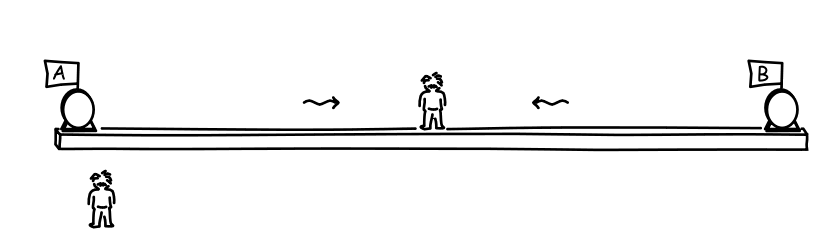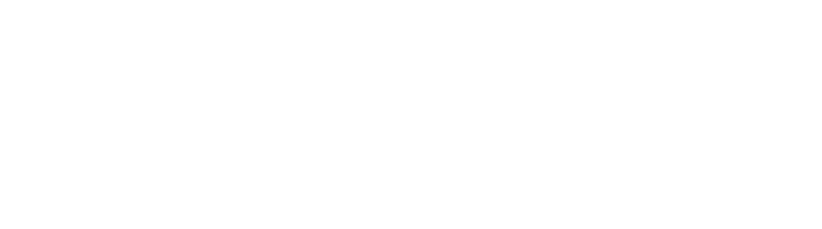
Here's a version that isn't animated. Earlier times are depicted lower in the figure.

So far, nothing remarkable has happened. That is about to change.

Now consider this process from the point of view of an observer who moves relative to the platform along its length. For that new observer, the platform moves rapidly and, in the animation, in the direction from A towards B. Once again there will be two flashes and light from them will propagate towards the observer at the midpoint of the platform. However the midpoint is in motion. It is rushing away from light coming from A; and rushing toward the light coming from B. Nonetheless, the two signals arrive at the midpoint at the same moment.

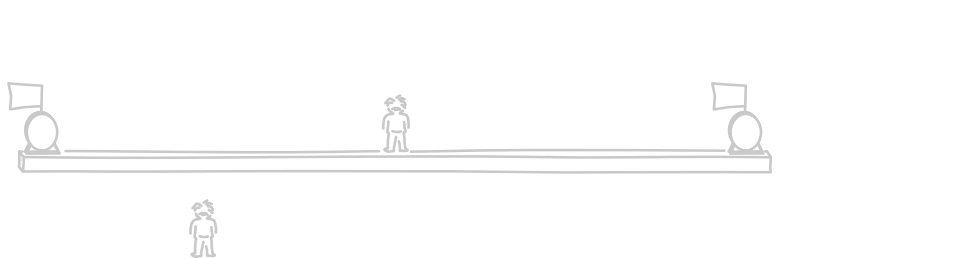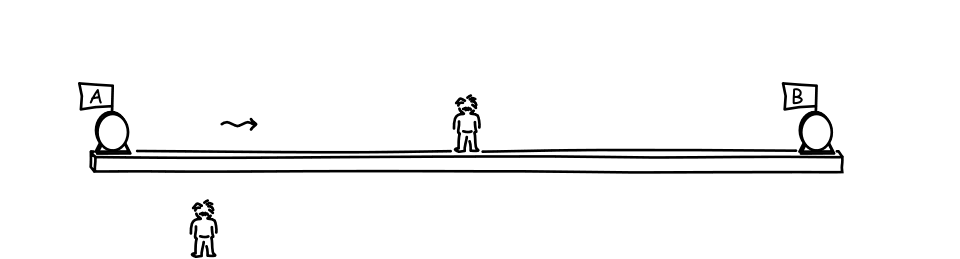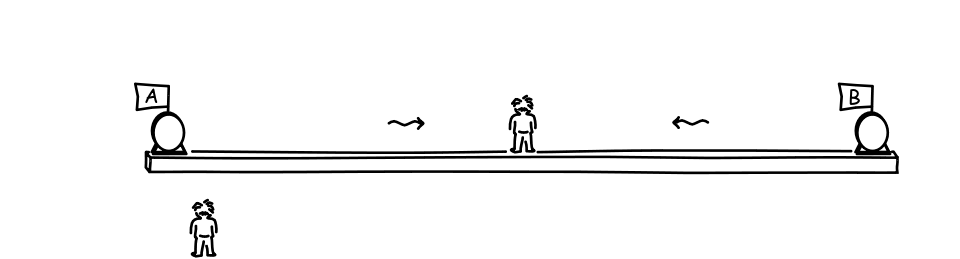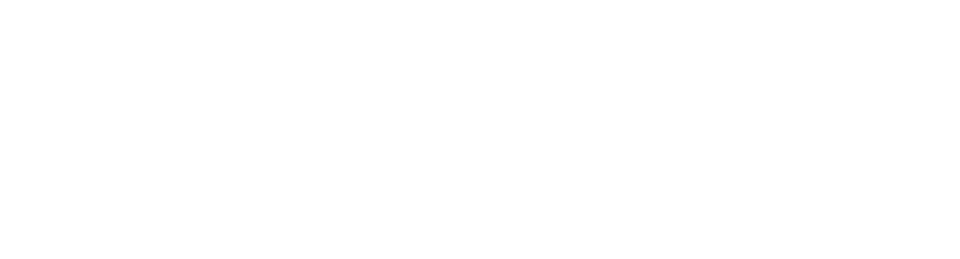
Here's a version that isn't animated. Earlier times are depicted lower in the figure.

The reasoning extends to the clocks. The clocks at A and B show the same time "0" when the flash events happen at each. These two events are not simultaneous for the new observer. Therefore the new observer will judge the clocks at A and B not to be properly synchronized. In fact clock A is set ahead of, that is, earlier than clock B, for it reads "0" earlier than clock B.

Relativity of Simultaneity without Light Signals

The effect just described is the relativity of simultaneity. The account above uses light signals merely as a means to enable the two observers to determine the time order of the events. The light signals themselves are not an essential part of the effect and they can be distracting. We can describe the effect without them as follows.

On the platform, we have two events.
The A-event at the A-end of the platform coincides with the setting of the A clock to 0.
The B-event at the B-end of the platform coincides with the setting of the B clock to 0.
So far we have said nothing about the order in time of these two events.

Two observers in relative motion disagree on the timing of the two events and on the associated synchrony of the clocks.

We shall take the case in which a platform observer judges the A- and B-events to be simultaneous and the A-clock and B-clock to be properly synchronized.

Then an observer moving relative to the platform and with motion parallel to it judges that:
-- the trailing A-event at the rear of moving platform occurs earlier; and the A-clock is set earlier than the B-clock.
-- the leading B-event at the front of the moving platform occurs later; and the B-clock is set later than the A-clock.

The simple rule to help you keep track of which event happens when in this particular situation is this:

trailing event ↔ earlier
leading event ↔ later.

We can make the result of the relativity of simultaneity more precise with a simple quantitative rule. (We will not be using this rule later, but it is included here for completeness.) Imagine that we have a long platform moving inertially with respect to some inertial rest frame. To make the result more definite, assume that there is a long ruler at rest in this moving frame with distance markers as indicated in the figure below. A clock is placed at each distance marker. If these clocks are synchronized according to the judgments of simultaneity of the moving frame, the clocks will be poorly synchronized according to an observer in the inertial rest frame.

According to the judgments from this resting frame, at some fixed moment of time in the rest frame, the trailing clocks of the moving system will read a time later than the leading clocks of the moving system. This follows since events that are simultaneous in the resting frame are judged to have happened earlier in the trailing part of the moving system and later in the leading part.

The amount of dislocation in time of the clocks from the clock at the center conforms with one of the simplest rules possible. This amount varies linearly with the distance as measured in the moving frame. That is, if you double or triple the distance of the clock from the clock at the center of the moving frame, the amounts of dislocation are doubled or trebled. The amounts also increase linearly with speed. Double or treble the speed of the moving frame with respect to the resting frame and the amounts of dislocation at similarly measured positions are doubled or trebled.

Since it is so simple, it is worth writing down the formula that captures these dependencies. It is:

Dislocation in time = — speed x distance / c²

Here "speed" is the speed of the moving frame of reference and "distance" is the distance as measured in the moving frame from the center point. Positive distances are towards the leading edge. Negative distances are towards the trailing edge.
Here are the calculations that yield this formula.

"Only Apparently Irreconcilable"

The notion of the relativity of simultaneity brought an immediate benefit for Einstein in his setting up of the special theory of relativity. He had noted in the introductory remarks in his 1905 paper that the principle of relativity and the light postulate are "only apparently irreconcilble." The relativity of simultaneity solves the problem and secures that compatibility.

To see how that works, consider how we arrived at the relativity of simultaneity. The key to the analysis above was that the speed of light is same value c in all inertial frames. That is, we found:

The constancy of the speed of light as measured by any inertially moving observer entails the relativity of simultaneity.

We can turn that around and get the reversed result. The puzzle for an inertial observer is to understand how it is possible for a moving observer to recover the same speed c for light signals, even though that observer is moving. The puzzle is solved by considering how an inertial observer judges the clocks in the moving system to be dislocated in time, according to relativity of simultaneity. That dislocation is just the right amount needed for the moving observer to determine that light signals are moving at c.

That is, we have:

The relativity of simultaneity entails that all inertial observers will measure the same speed c for light.

Who is Right?

The two observers disagree on the timing of the events and the synchrony of the clocks. It is easy to imagine that one of them has made a mistake and the other is right. That would be comfortable for it would require no adjustments to our concept of time. However, NEITHER has made a mistake or has been somehow misinformed. Rather it is that judgements of the simultaneity of spatially separated events depend on the motion of the observer, just as the rates of clocks and lengths of bodies depend on the motion of the observer in special relativity.

There is no absolute fact as to whether two spatially separated events are simultaneous. There is only a fact of simultaneity or its failure relative to an inertial frame of reference.

That a moving clock slows and moving rod shrinks is something most of us get used to with a little thought. The same is not true of the relativity of simultaneity. It is harder to get used to it, since it amounts to a more fundamental breakdown. It tells us that that there is no absolute fact about the relative timing of events at distant places. Imagine that you have candles on a birthday cake in Pittsburgh and on one in far-away Sydney. You plan to have them blown out at exactly the same moment. The relativity of simultaneity tells you that there is no absolute fact to whether you succeed. Relative to an earth-bound observer, you may succeed. But that can mean that relative to an observer on the moon, who moves relative to the earth, you did not succeed.

Image from http://en.wikipedia.org/wiki/File:Birthday_candles.jpg

The relativity of simultaneity adds to the repertoire of quantities that are relative and not absolute. There is no absolute fact to whether a spaceship is moving uniformly or is at rest. It can only be said to be at rest relative to another body. There is no absolute fact as to whether a rod is a foot long or a process lasts for one minute. They can only true with respect an observer with a definite state of motion. To this list we add that there is no absolute fact to whether two spatially separated events are simultaneous; or whether two spatially separated clocks are synchronous. These can only be true relative to an observer with a definite state of motion.

What the Relativity of Simultaneity is NOT

There is a quite benign way in which observers can disagree on the simultaneity of events. It is not the effect at issue. To see the benign way, imagine that a flash of lightning strikes some high point in a town, such as a tower or steeple. The strike comprises two events, one in light and one in sound: the flash of the lightning and the boom of the thunder. For someone in the tower or steeple, the two events are simultaneous. It would not appear so for someone standing on a distant vantage point, such as another distant tower or steeple, watching the lightning strike. That observer would see the flash and then, several seconds later, hear the boom of the thunder. For the first observer the flash and the boom are simultaneous. For the distant observer they are not simultanteous; or, more precisely, they do not appear simultaneous.

This same effect can arise in more abstruse settings. When we look at a distant galaxy 500 million light years away, we are seeing it as it appeared 500 million years ago. If we now see some cataclysmic event occurring now, such as two of these galaxies colliding, that event really happened 500 millions years ago. It will appear to us that it happened now, at the same time as the events of the present day. In fact it did not. We know that and we correct for the time the starlight took to reach us when we judge the timing of the event.

NASA reports of this image: "The collision between the two parent galaxies produced a shockwave effect that first drew matter into the center and then caused it to propagate outwards in a ring. ... Arp 148 is nicknamed Mayall's object and is located in the constellation of Ursa Major, the Great Bear, approximately 500 million light-years away." https://www.nasa.gov/multimedia/imagegallery/image_feature_2085.html image at https://www.nasa.gov/sites/default/files/images/597502main_hs-2008-16-aa-xlarge_web_full.jpg

These two examples illustrate the oddities of what we can call "appearance simultaneity." Events are simultaneous in this sense, merely if our sensations of them happen at the same moment. Or they fail to be simultaneous in this sense if our sensations of them happen at different times.

That sort of simultaneity is not the sort that is at issue in the relativity of simultaneity. The idea is that we correct for differences in appearance simultaneity. For example, when we hear the boom of the thunder coming after we see the flash of the lightning, we routinely allow for the fact that light travels very rapidly, but sound travels slowly--roughly one mile in five seconds. So even though we sense the flash and boom at different times, we judge the two originating events to be simultaneous.

Here's another case. Two lightning bolts strike at points D and E, where D is farther away from the observer. Let us imagine that the strikes are timed so that light signals from the bolts arrive at the same moment at the observer. The observer would see both flashes at the same time. The bolts would appear simultaneous. But the observer would then correct for the greater distance that the light signal from D must travel. That the observer sees the flashes at the same time would mean the observer would judge the D bolt to have struck earlier than the E bolt.

The relativity of simultaneity of relativity theory arises after we have corrected for the oddities of appearance simultaneity. Even after those corrections have been made, it turns out that observers in relative motion will not agree on the timing of spatially separated events. In the thought experiment above with the A and B clocks, it turns out that no corrections for appearance simultaneity are needed. Since the observer is located at the midpoint of the platform, the flashes of light at A and B are delayed equally. That is why the observer was placed there.

It is easy enough to see how the thought experiment would be altered if the platform observer were not located at the midpoint.  Consider, for example, the case in which the platform observer is placed 1/4th the way along the platform, on the A-clock end of the platform. As before, light signals are emitted at the same time according to the judgments of simultaneity in the platform frame of reference, as shown in the figure.

Since the platform observer is now placed closer to the A-clock, the light signal from the A-clock will reach the platform observer first; and the light signal from the B-clock will arrive later. Because the platform observer is not located at the midpoint, the observer will make corrections for the different times of flight of the two light signals.

• To reach the observer, the light signal from the B-clock must cover three times the distance compared to that which must be covered by the signal from the A-clock.

• It follows that the light signal from the B-clock will take three times as long to reach the observer as will the signal from the A-clock.

Using these different times of flight, the platform observer makes the appropriate adjustments to determine when the light signals were emitted.

• The signal from the A-clock took 1 unit of time to arrive and arrives when the A-clock reads "1." Thus, the signal was emitted when the A-clock read "0." 

• The signal from the B-clock took 3 units of time to arrive and arrives when the B-clock reads "3." Thus, the signal was emitted when the B-clock read "0."

That is, the two light signals were emitted at the same time, "0"; and the two clocks are correctly synchronized.   

What you need to know:

• What the relativity of simultaneity is.
  
• What the relativity of simultaneity is not.