
John Wheeler with Hideki Yukawa and Einstein
| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
| Black holes are some of the most interesting pathologies in space and time delivered by Einstein's general theory of relativity. They form when matter collapses gravitationally onto itself, such as when massive stars burn out. They are a region of space where the gravitational pull is so strong that nothing--not even light--can escape. Hence John Wheeler called them "black holes." There is more. They incorporate singularities in spacetime structure: points where Einstein's theory breaks down, since the curvature of spacetime becomes infinite. And they can supply bridges to new universes |  John Wheeler with Hideki Yukawa and Einstein |
We tend to associate black holes with Einstein's general theory of relativity. Yet their origins lie firmly in classical, Newtonian physics. They depend on a potentially catastrophic instability that resides merely in the fact that masses attract gravitationally and attract more strongly the closer together they are. So once gravitational collapse starts, its gets harder and harder to stop. This means that fully collapsed bodies that don't allow light to escape are already possible in Newtonian theory.
So far we only have a singular gravitational field. Newton's space and time are unaffected. Now add the idea brought by general relativity that gravity goes with a curvature of spacetime. We find that a singularity in the gravitational field corresponds to a singularity in the structure of space and time itself.
Black holes tend nowadays to be accepted as a routine part of physical theory. That certainly was not always so. Theorists of earlier decades viewed them skeptically. Peter Bergmann, one of Einstein's assistants, remarked that through such singularities, general relativity contains the seeds of its own destruction. As we shall see in the next chapter Einstein himself tried to argue (unsuccessfully) that they could not form.
Now we are so confident that there are black holes that the issue is not so much whether they exist, but where we should point our telescopes to see one. They arise either as collapsed stars or as the massive centers of galaxies. The object Cygnus X-1 has long been a strong candidate for a black hole. It is an unseen companion to a visible star that is 33 times as massive as our sun. The star HDE 226868 orbits around a second object so massive and compact that it must be a black hole. That object is Cygnus X-1, a strong candidate for a black hole.
Here is an image of HDE 226868 and its invisible companion taken with an optical telescope at the Palomar Observatory (http://imagine.gsfc.nasa.gov/YBA/cyg-X1-mass/cygX1-image.html)

Here's an artist's impression of Cygnus X-1, whose powerful gravity drags matter from its companion star into the black hole accretion disk. (http://agile.gsfc.nasa.gov/docs/objects/binaries/cygx1_artists.html)
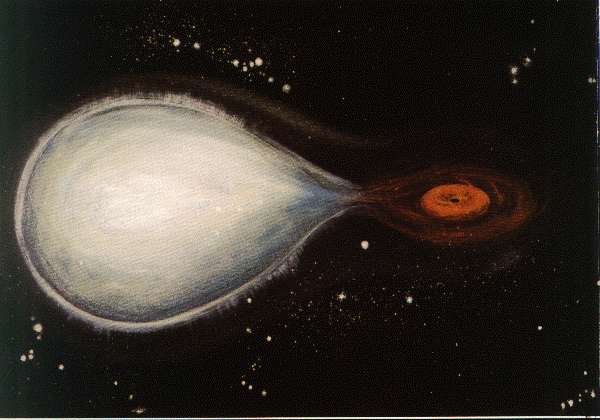
| The process is more dynamic. The two objects orbit each other with a period of 5.6 days as this sped up animation shows (http://heasarc.gsfc.nasa.gov/docs/binary.html). |  |
The images above were drawn from the NASA website, http://www.nasa.gov/, January 21, 2007. NASA provides these images copyright free subject to the restrictions on http://www.simlabs.arc.nasa.gov/copyright_info/copyright.html
The considerations above were the early steps in the identification of black holes. Since then, much has happened. We now know that there are many more black holes scattered throughout space. There is a giant black hole at the center of our galaxy. On September 14, 2015, the LIGO project ("Laser Interferometer Gravitational-Wave Observatory") detected the distinctive "chirp" in gravitational waves emitted by two black holes collapsing together. Their announcement.

This image is a still from a video simulation of what the coalescence of two black holes would look like. See video.
In April 2017, the Event Horizon Telescope combined signals from several widely spaced X-ray telescopes to produce an image of the black hole at the center of the M87 galaxy, 55 million light years from earth. The black hole is 6.5 billion times as massive as our sun. Here is their famous image. The shadow of the black hole is in the center.

Stable systems are inherently self-correcting. If something disturbs them from their equilibrium state, they naturally correct themselves and return to the equilibrium.
| Consider a heavy office desk. Lift the corner and release it. It falls back to its regular position. It's weight is so positioned that it corrects deflections from the normal position. Things do not spontaneously get hot. If we heat something, it tends to lose heat faster as it gets hotter. Heat a potato in the oven and we can only keep it hot by leaving it in the oven; it spontaneously cools once we take it out. |
An example closer to what is to come is electric charges. They naturally tend to distribute themselves. If we clump a lot of positive charges together, they repel, opposing the clumping. The more we force them together, the stronger the forces of repulsion become. The more they resist.
Unstable systems are not self-correcting under perturbations. They are the opposite. If we disturb them, their natural dynamics magnifies the disturbance.
| Consider a tall, thin bookcase. It is not stable. If we tip it away from its normal upright position sufficiently far, it will fall. Once the center of the weight passes the support, the weight no longer acts to oppose the deflection; it reinforces it. The deflection grows and the greater the deflection, the faster it grows. |
If temperature behaved similarly, our world would be very different. Imagine that, once a body got hot enough, that would somehow trigger it getting yet hotter, and so on indefinitely. We would be standing forever on the abyss of possible runaway processes that yield infinite temperatures.
Now consider gravitational collapse. As Newton first told us over 300 years ago, all bodies gravitationally attract all other bodies. So matter naturally wants to clump together in ever denser, smaller clumps. This process is gravitational collapse.
It is not a self-limiting process. The more matter clumps together, the stronger become the forces that drive the clumping. That is an immediate consequence of Newton's inverse square law. The gravitational force between bodies varies inversely with the square of the distance between them.
As two bodies near and the distance between them reduces from 3 to 2 to 1, the gravitational force pulling them together increases ninefold: from 1/9 to 1/4 to 1.
The same thing happens if we have a large sphere
of matter collapsing gravitationally.
| The figure shows the force on a unit of mass
located at the surface of the sphere. As the size of the sphere
reduces from 3 to 2 to 1, the force on the unit mass at the surface
increases ninefold: 1/9 to 1/4 to 1. For experts only: It is not immediately obvious that this follows from Newton's inverse square law since the force on the mass at the surface will be the total force due to all the other masses in the sphere. These other masses are at many different distances from the unit mass and the forces due to each must be summed. A familiar theorem in Newtonian mechanics tells us that the gravitational force of masses in a sphere on bodies outside it is the same as the force due to a point with equal mass located at the sphere's center. So we can figure out the force on the unit mass by pretending that the masses of the sphere are all located at its center. |
In short, if we have a cluster of masses that fall together under their mutual gravitational attraction, those forces of attraction will grow stronger as the masses come closer together. There is nothing in the properties of gravity to prevent the continued collapse. In this sense, gravitation forever threatens a catastrophic, runaway collapse.
The process of gravitational collapse just described is the process by which stars, galaxies and planets are formed. Cosmic debris, hydrogen or other elements, coalesce under their own gravity to produce these celestial objects. What prevents their collapsing to a point? Other forces intervene.
There are three types of forces that halt continuing collapse. Each force has its limit.
| Gravitational collapse of... | is halted by... | But that halting force can be overcome by... | |
 |
Galaxies and planetary systems. Their matter forms great, orbiting swirls as they collapse together. |
The orbital motion of stars in galaxies and planets in solar systems lead to centrifugal forces that prevent the stars and planets falling to the centers of the systems | If these motions are lost due to collisions, collapse can ensue. |
 |
Stars. They become very hot as they form from gravitationally collapsing clouds of cosmic matter. |
Their high temperatures yield high pressures that balance the continuing pull of gravity. | Stars are radiating away their heat. Even though nuclear reactions contribute more heat, eventually they will burn out and the stars will cool. |
 |
Planets. | The mechanical rigidity of the rocks and incompressibility of the molten core of rocky planets prevent further collapse. The gas pressure of gas giants prevent their collapse. | If the gravitational forces are strong enough because a lot of matter is collapsing, these mechanical forces can be overcome. |
The table summarizes how three different effects prevent complete gravitational collapse. The circumstances with stars needs a little more explanation.
Stars are huge spheres of gases, heated to very high temperatures by the energy released in gravitational collapse and then by thermonuclear reactions ignited by the rising temperatures. Those high temperatures cause the gases to expand. If those expanding gases were somehow trapped in a chamber so the expansion was halted, very high pressures would result. The gravitation of the star itself provides just such a chamber. The gravitational attraction of each part of the star for all other parts pulls back on the other parts, stopping the expansion and producing high pressure.
The stability of the star consists in a perfect balance of the outward pressure forces and the inward gravitational forces. It is a temporary balance, since the nuclear fuel of the stars will eventually burn out.
What makes black holes black is that light cannot escape
from them. In this regard, there is a simple analog
to the black holes of general relativity in Newtonian physics. It is a commonly discussed analog, but must be approached with caution since a Newtonian black hole is quite unlike relativstic black holes in many of its properties.
•
It is like a relativistic black hole in the sense that light, conceived as a Newtonian ballistic particle, cannot escape it.
• it is unlike a relativistic black hole in the sense that non-ballistic bodies, such as fueled rocket ships can in principle always escape it.
The analogy is popular since, in one of those curious accidents of physics, some of the formulae come out to the be same in the Newtonian and relativistic cases, even though their physical interpretations are very different.
So, let's get started.
One way to gauge the intensity of the gravitational field
of a collapsing body is to determine its "escape velocity." If we have an
object on the surface of one of these entities and hurl it straight up,
the escape velocity is the minimum speed it
would need in a vertical direction to escape the gravitational pull of the
entity. On the surface of our earth, that escape velocity is 11 kilometers
per second vertically--a quite prodigious speed.
That means that a body hurled directly upward at more than 11 kilometers per second would escape the pull of the earth's gravity with some speed to spare. An object hurled upward at less than 11 kilometers per second would always fall back. The closer the speed gets to 11 kilometers per second, the higher the object would rise before falling back. At 11 kilometers per second, the object has exactly the minimum velocity needed to escape the earth; once it was far away from the earth, all its velocity would be used up by the escape and it would approach rest.
|
Here is what happens when the object
is not given enough vertical speed to escape the earth. |
Here is what happens if the object
is flung more powerfully. |
The idea of being shot out of a canon as a way of escaping our earth has a venerable place in science fiction. It is how Jules Verne imagined that we might take a trip to the moon in an 1865 novel.
 |
 Click here for 7MB animation from George Melies' 1902 movie of Jules Verne's story of a trip to the moon. |
If the earth were to undergo gravitational collapse, that
escape velocity would increase as the collapsing
earth's size decreases. The increase is not as fast as you might
expect. It grows only with the square root of the change in size. The
table illustrates this growing.
| Decrease size by ratio: | Increase escape velocity by ratio: |
| 100 | 10 |
| 10,000 | 100 |
| 1,000,000 | 1,000 |
| So reduce the radius of the earth by a factor of 100 (from 6500 kilometers to 65 kilometers) and the escape velocity increases by a factor of the square root of 100; that is, by a factor of 10. So it becomes 110 kilometers per second. | The precise formula, if you want to
know, is just |
To see the formation of a Newtonian black hole, just continue this collapse process, as in the figure. The Newtonian black hole forms when the collapsing earth's radius passes 1/3". That is an astonishingly small size into which all the matter of the earth must be squeezed. But if it is done, the gravity at the surface is so strong that an object hurled upward at c=300,000 km/sec=186,000 miles/sec could only just escape. Nothing traveling any slower could escape. If the collapse continued to anything smaller than 1/3", then not even objects moving at c could escape.
| The object formed with radius 1/3" from the earth
is a Newtonian black hole. It has many properties in common with the
black holes of general relativity. Most importantly, they both have
the same size.
As the collapse proceeds, energy is released in larger and larger amounts. If the collapse continued to a point, an infinite amount of energy would be released (but would not be carried off by light moving at c!). |
For experts only. The formula for the size rbh
of a Newtonian black hole is easy to compute. The potential energy
of a mass m on the surface of a sphere of mass M and radius rbh
is negative and is just -GMm/rbh, where G is the
universal constant of gravitation. If the mass m moves at speed c
directly upwards, it has kinetic energy (1/2)mc2. If the
mass is just able to escape, these two energies must sum to zero.
Solving we find rbh = 2GM/c2 Curiously, this is the same formula as general relativity gives for the "Schwarschild radius" that designates the event horizon of a general relativistic black hole. |
The existence of the Newtonian black holes and their similarities to the black holes of general relativity is striking. However the significance of their similarities should not be overestimated.
Light cannot escape a Newtonian black hole only if a particular way of escaping is chosen and particular assumptions are made about light: that the light can only escape if it is shot directly upwards like a stone from a catapult and if the maximum speed it has when released from the catapult is c. Newtonian physics would allow things to escape the Newtonian black hole by gentler means. Imagine a rocket ship that fires its motors so as to generate an upward acceleration that is greater than the attraction of gravity. As long as that upward acceleration just exceeds that of gravity, the rocket ship would gently rise and escape. That is not possible, as we shall see, for a black hole in general relativity.
We need not fear that our planet earth will undergo gravitational collapse. The mechanical incompressibility of rock is an enduring feature.
It is not so for stars, such as our sun. The gas pressure that resists collapse depends on the high temperature of the star. Stars radiate and constantly lose the energy that sustains the high temperature. That energy is resupplied by nuclear reactions in the star. When stars form initially from collapsing clouds of hydrogen gas, the hydrogen fuses to form Helium, liberating vast amounts of energy. After that, more fusion reactions occur producing more elements.

https://images-assets.nasa.gov/image/GSFC_20171208_Archive_e001435/GSFC_20171208_Archive_e001435~large.jpg?w=1920&h=1920&fit=clip&crop=faces%2Cfocalpoint
These reactions cannot proceed indefinitely. Eventually the nuclear fuel will be spent and the gases will start to cool. When they do, the pressure produced by the high temperature will drop as well. And when that happens, the balance of inward gravitational force and outward pressure will be disrupted in favor of the gravitational forces. The star will begin to collapse in onto itself. The stability of stars is only a temporary circumstance.
What happens next is not so simple. There are many possibilities and astrophysicists have developed detailed histories of how different stars will fare under gravitational collapse.
The most important factor in deciding their fate is the mass of the star. The unit commonly used is "solar mass"--the mass of the star in relation to our sun's mass. "Two solar masses" means twice the mass of our sun. Smaller stars tend to burn out quietly, larger stars are more likely to collapse catastrophically and produce a black hole. The table summarizes some of the major trends.
| Stars of.. | In gravitational collapse... |
| Less than 1.3 solar masses. | Form black dwarves. |
| 2 to 3 solar masses. | Form neutron stars ("pulsars"); or may fragment in supernova explosions. |
| More than three solar masses | Nothing halts gravitational collapse; black holes form. |
While the eventual fate of our sun is clear, we are in no immediate danger. The times required for these processes is of the order of billions of years. Our sun has been gently burning its hydrogen for 4.5 billion years and will continue to do so for another 5 billion.
One might expect that larger stars would live longer since they have more fuel. However the reverse is true. They burn their nuclear fuel even faster so they have shorter lives.
Black holes can form in both Newtonian theory and general relativity. However there are significant differences between them.
| Newtonian black hole | Singular point of infinite matter density and field strength. | Space and time unaffected. | Infinite energy is released in the collapse that forms the black hole. |
| General relativistic black hole | Singularity in spacetime curvature. | Causal structure of space and time affected; there are causally isolated regions of space and time. | Finite energy is released in the collapse that forms the black hole. |
A Newtonian black hole is less radical than a relativistic black hole in so far as the Newtonian black hole involves no disturbance to space and time. Such a disturbance is inevitable in general relativity, since Einstein's gravitational field equations connect matter density and gravitation to spacetime geometry. So if the matter density and gravitational field becomes singular, we should expect similar pathologies in space and time.
A Newtonian black hole, however, is far more radical that a relativistic hole in another sense. In formation, a fully collapsed Newtonian black hole must shed an infinite amout of energy. While we talk of infinities all the time, we should not be casual about such an amount. The release of an infinity of energy in our neighborhood would overwhelm everything. In general relativity, the formation of a black hole does not call for an infinity of energy to be released.
Let us now trace how spacetime is affected by the formation of a black hole in general relativity. The spacetime diagram below shows a sphere of matter undergoing gravitational collapse. It is the simplest case of an uncharged, non-rotating sphere of matter and produces a so-called "Schwarzschild" black hole.
| At the bottom of the figure is a spatial slice of
a fairly ordinary spacetime, in which a sphere of matter begins its
gravitational collapse.
The collapse continues as we proceed up the figure. The sphere becomes smaller and smaller, until it eventually it is so small and dense and its gravity so strong that not even light can escape its surface. That is the formation of a black hole and it happens at a radial position known as the "Schwarzschild radius." For an object the size of the earth, we already saw that radius is 1/3". For an object the size of the sun, it is 2.95 km. (Note that neither the earth nor sun have enough mass to overcome stabilizing forces and produce a black hole.) The radial position from where light can longer escape is called the "event horizon." It is an important boundary in spacetime. Outside the event horizon, rapidly moving bodies that have strayed too close to the black hole can still escape, if they can move fast enough. Once they stray within the event horizon, no escape is possible. The fastest speed relativity theory admits, that of light, is no longer enough to allow escape. Once the collapsing matter has collapsed within the event horizon, the collapse continues all the way to zero size. What results is a point of infinite matter density and therefore a point of infinite spacetime curvature. It is a singularity. Once these two quantities have become infinite, Einstein's gravitational field equations have ceased to function; the theory breaks down. Within the event horizon, all motion of matter and light is towards that singularity. It is everyone's future. In this sense, the directions of space and time are switched within the event horizon. Time now points towards the singularity, for that is everyone's future. |
In a Minkowski spacetime, the light cones mapped out the possible motions and the possibilities for causal connections. In that spacetime, the lightcones were uniformly distributed in spacetime, with no regions of spacetime causally distinct from others. In a black hole, it is otherwise.
| In a black hole spacetime, lightcones far away
from the event horizon are oriented as expected.
As we near the event horizon, the light cones tip over to face the singularity. At the event horizon itself, the light cones have tipped over so far that only motions faster than light can escape falling into the singularity. Within the event horizon, the light cones futures are all pointed towards the singularity. |
A presumption in the literature on black holes is that nothing travels faster than light. We noted earlier that relativity theory does in principle admit faster than light motions--a particle executing them would be a tachyon. However no such particle has been detected.
When we look at these diagrams, it is clear that the event horizon marks a special boundary in spacetime. It marks the point of no return for travelers falling into the black hole. However there is nothing special, locally, at the event horizon that is different from neighboring events. As the traveler passes the event horizon, there are no special flags or markers that the traveler sees. Spacetime around the event horizon will be highly curved but otherwise no different from the spacetime on either side. In brief, the traveler "feels no bump" when the event horizon is passed.
The event horizon gets its special properties from its relation to the global structure of the spacetime and specifically to the singularity and the exterior of the black hole. For it marks the boundary past which a traveler's future must lie in the singularity and can no longer lie in the exterior of the black hole. It is something like the position computed by demographers called the "mean center of the US population." When you stand at that position, which is somewhere in Missouri, the average distance to all peoples in the US comes out to zero. Move an inch to the west and you are now on average closer to people in the west; move an inch to the right and you are now on average closer to people in the east. Of course it is nothing locally about the position in Missouri that gives it this property. It is the relation between that position and all the people spread out over the US.
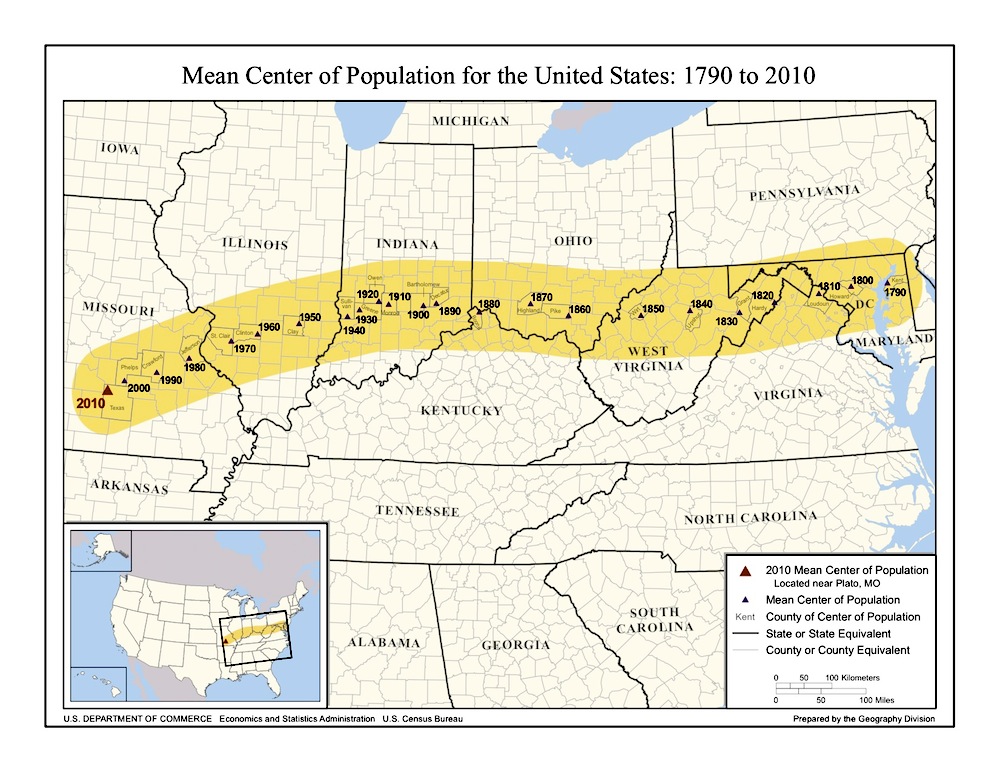
Image source: US Dept of Commerce, US Census,
http://www.census.gov/geo/www/2010census/centerpop2010/centerpop_mean2010.pdf
What would it be like to fall into a black hole? In brief, it would be a mistake one would not want to repeat--although you would not get the chance to repeat it!
The figure shows the worldline of a planet near a black hole and the worldline of a spaceship that imprudently came too close to the black hole and fell in.
The first part of the curve represents that portion of the spaceship's motion that an observer outside the black hole would see. The spaceship would fall rapidly at first towards the black hole. However, as it got closer, it would slow and eventually freeze just outside the event horizon. In the entire lifetime of the outside observer, the body would never actually reach the event horizon. That would be true even if the planet observer lived and observed indefinitely.
All this would be hard to see. Other objects falling into the black hole would be emitting bursts of radiation that would blanket the observer's view. Also, as the spaceship gets closer to the event horizon, light from it would be ever more red shifted and thus weakened and dimmed.
The view of this journey for the spaceship in would be quite different. The outside world appear to speed up and huge amounts of outside time would elapse in the short time the spaceship would take to reach the event horizon. The observer would pass the event horizon feeling no bump in spacetime at all. The final stage of the journey would be completed extremely rapidly as the spaceship reached the singularity.
The diagram is not a good representation of the journey. The spaceship's trajectory is shown in two disconnected parts. It is not that the figure is truncated at the top in a way that hides the place where the two parts connect. If we drew extensions of the figure upward, the two parts of the trajectory would never connect, no matter how great the extension. This is a seriously misleading aspect of the figure. In fact the worldline is a continuous trajectory in spacetime with no break.
A note of explanation for more expert students.
The diagram above depicts a black hole. Our discussion of it shows that the diagram is, in an important aspect, a quite poor representation of the black hole. How did this happen? The diagram arises from a direct translation of the original formula used to specify a Schwarzschild spacetime. That formula used four coordinates to label events: t for time, r for radial distance from the center and two angle coordinates θ and φ that specify the spatial direction of an event around the center. The important work is done by the t and r coordinates. The diagram arises by plotting the t coordinate up the page and r coordinate across the page. In simpler cases, such as a Minkowski spacetime, this sort of translation is benign. The direction up the page is always timelike in the spacetime geometry and the direction across the page is always spacelike.
This benign translation is no longer the case for the formula used for the Schwarzschild spacetime. It results in a diagram divided into two parts. The up direction outside the event horizon is timelike, but the up direction becomes spacelike within the event horizon. The region marked as the event horizon itself properly belongs to neither region since terms in the formula for the Schwarzschild spacetime become singular at the region marked as the event horizon.
For those who want to know it, the formula for the spacetime interval s for a black hole of mass M in suitable units is:
ds2 = (1-2M/r)dt2 - (1-2M/r)-1dr2 - r2(dθ2 + sin2θdφ2)
The event horizon is at coordinate r = 2M, also called the "Schwarzschild radius." At this coordinate value, the coefficients for the dt2 and dr2 terms go to zero and infinity respectively. Passing across the r = 2M value, these coefficients change sign, which corresponds to the switch in the timelike and spacelike directions of the spacetime geometry.
In spite of its dubious geometric credentials, versions of the diagram shown above do appear in standard relativity texts, including one that was a landmark of mathematical precision, Stephen Hawking and George Ellis' Large-Scale Stucture of Spacetime. Cambridge University Press, 1973, p. 300:
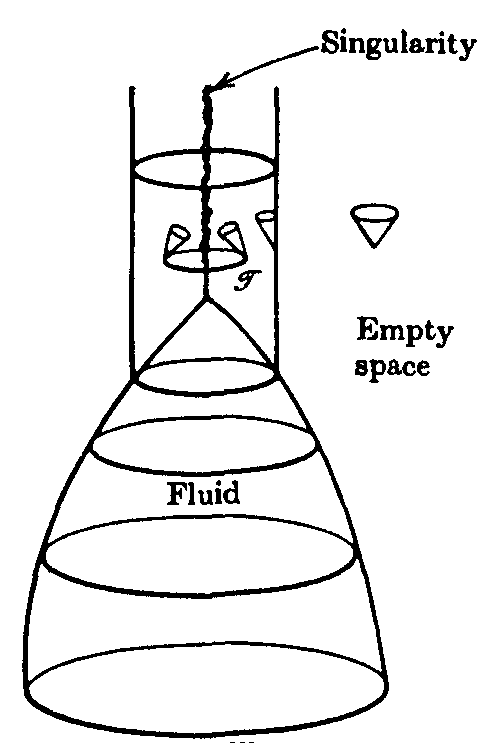
This figure is displayed as part of a critical analysis of Hawking and Ellis' text and, for this reason, is reproduced here within the scope of the fair use provision of copyright law.
We shall see in the next chapter that Einstein treated the event horizon = Schwarzschild radius as singular precisely because he took seriously the singularity in the formula above. We now discount this singularity as an artefact of a coordinate system ill-adapted to this portion of spacetime.
The experience for the occupants within the spaceship falling in would be rapid. But it would not be pleasant. The reason is tidal forces.
When we stand on the earth, our feet are slightly closer to the center than our heads. So the gravitational force on our feet is slightly greater than on our heads. These differences of forces are known as tidal forces since they also produce the earth's tides. On earth the effect is so slight that we cannot perceive it.
| If we were to fall feet first into a black hole,
it would be quite different. Once we are close to the black hole,
the gravitational pull at our feet would be very much greater than
at our heads. We would literally be pulled
apart by the difference, as cruelly as if we were placed on
a medieval torture rack that stretched our feet from our heads. In science fiction movies of spaceships falling into black holes, these tidal forces are usually represented as rather interesting optical effects, somewhat like looking at a distorted reflection in a fun house mirror. The voyagers emerge merely ruffled as if they had enjoyed a rather energetic roller coaster ride. In gruesome reality, they would be lucky to be anything other than a bloody pulp. This gruesome end would likely be painless. The time taken between the onset of painful tidal forces and termination in the singularity turns out to be independent of the mass of the black hole. A plausible computation puts it at 0.067 seconds. it is less than the time a pain nerve signal takes to propagate to the brain. The calculation is in Thomas A. Moore, A General Relativity Workbook: Instructor's Solutions Manual. University Science Books, 2013, Problem 19.9, p. 158. I thank Joshua Norton (no relation) for pointing out this calculation. |
These tidal forces may seem familiar. Recall that we gauged
the curvature of space-time sheets by the extent to which free
fallilng bodies converged or diverged. These convergences and divergences
are experienced by the falling bodies as driven by external forces and
they are the tidal forces in question here.
They are called "tidal" because they are
responsible for the ocean tides on earth. Our planet is in free fall
toward the moon. The portion of the ocean's water closer to the moon
experiences a stronger attraction than the portion furthest away. That
elongates the waters that jacket the earth into two lobes. The earth
rotates under these two lobes, once every day, producing two high tides.
