| HPS 0410 | Einstein for Everyone |
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Quantum theory has made many demands upon us. We need now to accept that physics is essentially indeterministic; that particles may be somewhere without being at any particular place; that they may have energy and momentum without having any particular value for them; and a host more non-classical oddities. Most of these ideas are simply unfamiliar conceptions and, in the end, the best thing is just to get used to the idea that world depicted by quantum theory is very different from the world delivered by our raw senses.
There are other problems in quantum theory that should not
be accommodated with this forgiving attitude. This chapter will develop
the one that it most prominent and has proven most
intractable: the measurement problem. It depends on the fact that
a quantum system can evolve in time in two ways.
One way, you will recall from the last chapter, is Schroedinger evolution,
in which the wave of the system propagates in the familiar manner of
waves.
The other way a quantum system can evolve in time is through the "collapse of the wave packet" that arises when we perform a measurement:
When will a wave packet undergo Schroedinger evolution or collapse? Earlier, we saw that there is only a rule of thumb to guide us. Schroedinger evolution arises when matter waves are left to themselves or when they interact with just a few others. Measurement arises when a matter wave interacts with a macroscopic measuring device. That means that a matter wave interacting with a photographic plate collapses. Sometimes it is said that the last collapse does not happen until an intelligent human agent actually looks at the plate. That last claim is extremely strange. Are we supposed to believe that human intelligence enters into the time evolution of fundamental particles in the same way as perturbing fields?
The lack of a precise principle to decide which evolution will arise has created a constellation of puzzles known at the "measurement problem." The best known example is "Schroedinger's cat," a thought experiment devised by Erwin Schroedinger in 1935.
To see how it arises, let us first look at how quantum theory treats radioactive decay. The radioactive element Neptunium NP23193 is extremely unstable. It will undergo radioactive decay quite quickly.
It has a "half life" of 53 minutes. That means that if we start with a lump of NP23193 and wait 53 minutes we will have only half a lump left, near enough, and lot of radioactive decay products.
At the level of an individual atom of NP23193, that means that there is a probability of 1/2 that each individual atom will decay over this 53 minutes. Now, individual atoms of NP23193 are governed by Schroedinger evolution; the probabilities only enter when we measure to see if the atom has decayed or not.
So over 53 minutes the atom evolves into a half:half superposition of undecayed and decayed atom.
The collapse into one or other of these components only arises when we take a measurement. That may happen when we use a Geiger counter to check for radioactive decay products. If we find them, then the atom collapses into the decayed component. Otherwise it collapsed into the undecayed component.
https://commons.wikimedia.org/wiki/File:Geiger_Counter_(PSF).png
So far everything seems reasonable. What Schroedinger realized was that there was quite some arbitrariness in our division between Schroedinger evolution and wave collapse. It was quite possible for that one collapse to be magnified. The decay products of the one decaying atom might trigger the collapse of others. So instead of having just one atom entering into a superposition over 53 minutes, we might have very many atoms all coupled together entering the superposed state after 53 minutes.
The cat paradox arises when we push this process of amplification to an extreme. Instead of coupling the one atom of NP23193 to a collection of other radioactive atoms, we couple it to the 1025 atoms of cat. The coupling is simple, although cruel. A Geiger counter is set up to sense the decay of the atom. If it decays, the Geiger counter will trigger the opening of a can of poison. The atom, Geiger counter, poison and cat are all enclosed in a box.
We then wait 53 minutes. In that time, the atom evolves into a superposition of undecayed and decayed atom. With it, the poison evolves into a superposition of released and unreleased poison; and the cat into a superposition of live cat and dead cat.
+
At this stage, no measurement has been performed; no human has looked at the Geiger counter or listened for its clicks. So the cat is neither alive nor dead. The evolution, as far as the cat is concerned, is something like this:
Why
"something like"? It is because the proper representation is the one given
in the earlier figure. It is really still a superposition of two states:
Live cat-undecayed atom-unopened poison can
+
Dead cat-decayed atom-opened poison can.
What finally decides whether the cat is alive or dead is our observation. After 53 minutes we open the box and observe, that is, "measure," the life state of the cat. Only then does the cat's wave collapse onto one of dead or alive.
There is a widespread sense that there is something wrong with a theory that allows observation to play such an important role. Most people have an instinctive sense that the fact of life or death for the cat is not decided merely by our observation. After 53 minutes, the cat is definitely just one of alive or dead; whether we look in the box does not change that circumstance in any way.
This instinctive reaction is surely correct. However having it really only sharpens the problem. It does not solve it. For the inference that the cat is in a superposition of alive and dead follows directly from quantum theory by merely assuming that the box contains nothing but atoms whose time evolution is governed by Schroedinger's equation.
This paradox of the Schroedinger's cat is the most vivid expression of a lingering problem in the foundations of quantum theory. In the last two decades especially, there has been a huge amount of work devoted to finding variations to standard quantum theory or just new ways to think about the same theory that avoid this problem. There is no consensus on which approach is the correct one or even if some sort of repair is needed.
| Erwin Schroedinger published his "cat" thought experiment in a lengthy paper in the November 29, 1935, issue of the journal Die Naturwissenschaften. | Erwin Schroedinger, "Die Gegenwaertigen Situation
in der Quantenmechanik," Die Naturwissenschaften, 23 (1935).
pp. 807-12, 824-28. 44-49. |

| Here's the entirety of his original account of the cat: | Translation from Arthur Fine, The Shaky Game: Einstein, Realism and the Quantum Theory. University of Chicago Press, 1986, p. 65; excepting last two sentences. |

| "One can even make quite ludicrous examples. A cat is enclosed in a steel chamber, together with the following infernal machine (which one must secure against the cat's direct reach): in the tube of a Geiger counter there is a tiny amount of a radioactive material, so small that although one of its atoms might decay in the course of an hour, it is just a probable that that none will. If the decay occurs, the counter tube fires and, by means of a relay, sets a little hammer into motion that shatters a small bottle of prussic acid. When the entire system has been left alone for an hour, one would say that the cat is still alive provided no atom has decayed in the meantime. The first atomic decay would have poisoned it. The ψ-function of the total system would yield an expression for all this in which, in equal measure, the living and the dead cat (sit venia verbo ["pardon the expression"]) blended or smeared out. |  |
  unblurred cat from http://en.wikipedia.org/wiki/File:Cat_poster_2.jpg |
The characteristic of these examples that an
indefiniteness originally limited to atomic dimensions gets
transformed into gross macroscopic indefiniteness, which can then be
reduced by direct observation. This prevents us from
continuing naively to give credence to a "fuzzy model" as a picture
of reality. In itself this contains nothing unclear or
contradictory. There is a difference between a blurred or unsharply
taken photograph and a shot of clouds and mist.
" |
We are used to thinking of Einstein as a visionary who brought new and challenging theories of physics to us. However as the new quantum theory solidified in the late 1920s and thereafter became standard physics, Einstein increasingly found himself playing a rather different role, a critic of the new. He had no doubt about the great successes of quantum theory in exploring atomic phenomena and accommodating the results of experiments. His concern, however, was that the theory was only a provisional stopping point on the path to a better theory. We shall see in a coming chapter how Einstein elaborated these worries. He concentrated on the idea that the quantum wave was not a complete description of reality, but, in some way, merely described averages.
The best known expression of these worries came in a 1935 paper Einstein co-authored with Boris Podolsky and Nathan Rosen, known universally as the "EPR" paper. (A. Einstein, B. Podolsky, and N. Rosen, "Can quantum-mechanical description of physical reality be considered complete?" Phys. Rev. 47 777 (1935), pp. 778-80. Received March 25, 1935; published May 15, 1935.)
| In the aftermath of this paper, Einstein and Schroedinger exchanged letters in which they aired their common concerns about quantum theory. In that correspondence, Einstein put to Schroedinger what we now see is an early version of the cat paradox. He outlined a "crude macroscopic example" in a letter to Schroedinger of August 8, 1935: | Translation from Arthur Fine, The Shaky Game: Einstein, Realism and the Quantum Theory. University of Chicago Press, 1986, p. 78. |
"The system is a substance in chemically unstable equilibrium, perhaps a pile of gunpowder that, by means of intrinsic forces, can spontaneously combust, and where the average life span of the whole setup is a year. In principle this can quite easily be represented quantum-mechanically. In the beginning the ψ-function characterizes a reasonably well-defined macroscopic state. But, according to your equation, after the course of a year this is no longer the case at all. Rather, the ψ-function then describes a sort of blend of not-yet and of already-exploded systems.



Through no art of interpretation can this ψ-function be
turned into an adequate description of a real state of affairs; [for] in
reality there is just no intermediary between exploded and non-exploded.
"




Gunpowder image from
http://en.wikipedia.org/wiki/File:Pyrodex_powder_ffg.jpg Last fireball
public domain image at
http://www.wpclipart.com/energy/nuclear/nuclear_fireball.jpg.html
Perhaps Einstein's remarks led Schroedinger to his cat thought experiment; or perhaps his thinking was already moving in that direction. In a letter back to Einstein of August 19, 1935, he characterized his newly-conceived cat thought experiment as "very similar to your exploding powder keg."
| In 1946, Einstein wrote a scientific biography
for a volume dedicated to him. In the volume, he repeated his
concerns over quantum theory in the vein in which he'd conceived
them in the 1935 EPR paper. The volume included a large number of
papers authored by others in Einstein's honor. In 1949, Einstein
assembled his reactions to them. These reactions included a more
mature version of the gunpowder example, now modified by
Schroedinger's formulation. He took the example of the decay of a radioactive atom: |
Albert Einstein, "Remarks Concerning the Essays Brought Together in this Co-operative Volume," (1949) in, P. A. Schilpp, ed., Albert Einstein-Philosopher Scientist. 2nd ed. New York: Tudor Publishing, 1951. |
 |
"We
consider as a physical system, in the first instance, a radioactive
atom of definite average decay time, which is practically exactly
localised at a point of the co-ordinate system. The radioactive
process consists in the emission of a (comparatively light)
particle. For the sake of simplicity we neglect the motion of the
residual atom after the disintegration process. Then it is possible
for us, following Gamow, to replace the rest of the atom by a space
of atomic order of magnitude, surrounded by a closed potential
energy barrier which, at a time t = 0, encloses the particle to be
emitted. The radioactive process thus schematised is then, as is
well known, to be described — in the sense of elementary quantum
mechanics — by a ψ-function in three dimensions, which at the time
t=0 is different from zero only inside of the barrier, but which,
for positive times, expands into the outer space. This ψ-function
yields the probability that the particle, at some chosen instant, is
actually in a chosen part of space (i.e., is actually found there by
a measurement of position). On the other hand, the ψ-function does
not imply any assertion concerning the time instant of the
disintegration of the radioactive atom.
" |
| Here Einstein considered the quantum wave of a particle that will be emitted by a radioactive atom in its decay. The wave is confined inside the atom by a potential well. |
|
|
|
The potential well is not infinitely deep, so a part of the wave escapes and is outside the atom. If we measure the position of the particle outside the atom in this escaped part of the wave, we will with some probability detect the particle outside the atom. Radioactive decay will then have occurred. |
Einstein first diagnosed the difficulty as arising from a mistaken assumption that the quantum mechanical wave function, the ψ-function, gives a complete description of the one case, as opposed to an average over the descriptions of many cases. A few pages later, he then develops the example in the direction of Schroedinger's cat thought experiment as a response to the idea that we cannot ascertain a definite time of decay without making measurements that interfere essentially with the experiment:
"As far as I know,
it was E. Schrödinger who first called attention to a modification of this
consideration, which shows an interpretation of this type to be
impracticable. Rather than considering a system which comprises only a
radioactive atom (and its process of transformation), one considers a
system which includes also the means for ascertaining the radioactive
transformation — for example, a Geiger-counter with automatic
registration-mechanism. Let this latter include a registration-strip,
moved by a clockwork, upon which a mark is made by tripping the counter.
True, from the point of view of quantum mechanics this total system is
very complex and its configuration space is of very high dimension. But
there is in principle no objection to treating this entire system from the
standpoint of quantum mechanics. Here too the theory determines the
probability of each configuration of all its co-ordinates for every time
instant. If one considers all configurations of the coordinates, for a
time large compared with the average decay time of the radioactive atom,
there will be (at most) one such registration-mark on the paper strip. To
each coordinate configuration corresponds a definite position of the mark
on the paper strip. But, inasmuch as the theory yields only the relative
probability of the thinkable co-ordinate-configurations, it also offers
only relative probabilities for the positions of the mark on the paper
strip, but no definite location for this mark.
"
The single mark on the recording chart identifies a definite time of decay, analogous to the definite survival or death of Schroedinger's cat.
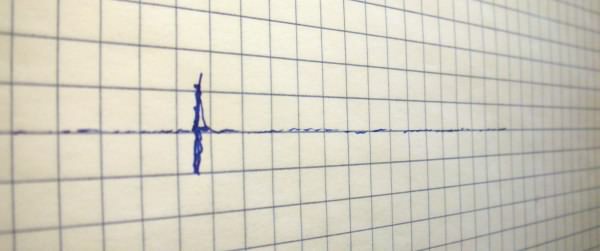
Yet the quantum mechanical formalism yields no single mark, but many marks, weighted probabilistically.

Einstein continued to explain that he regarded the standard quantum account of the mark as one for which "there is hardly likely to be anyone who would be inclined to consider it seriously."
"If we attempt [to
work with] the interpretation that the quantum-theoretical description is
to be understood as a complete description of the individual system, we
are forced to the interpretation that the location of the mark on the
strip is nothing which belongs to the system per se, but that the
existence of that location is essentially dependent upon the carrying out
of an observation made on the registration-strip. Such an interpretation
is certainly by no means absurd from a purely logical standpoint, yet
there is hardly likely to be anyone who would be inclined to consider it
seriously. For, in the macroscopic sphere it simply is considered certain
that one must adhere to the program of a realistic description in space
and time; whereas in the sphere of microscopic situations one is more
readily inclined to give up, or at least to modify, this program.
One of the largest of the recent literatures in philosophy of quantum theory has sought to resolve the measurement problem and we can only have the briefest glimpse of them here. Generally speaking, most of those responses fall into five groups.
1. Accept the standard account.
This response essentially urges that the standard treatment is adequate.
It is intelligible only in so far as it repeats the rule of thumb for
deciding when quantum systems evolve according to Schroedinger evolution:
Or when measurement collapse occurs:
This rule of thumb is adequate, perhaps, for practical physics. There is no doubt that a massive detector in a particle accelerator will engage in a measurement process. But a rule of thumb is less than the unambiguous rule that univocal theorizing requires. If you have a real interest in the foundations of quantum theory, you should not rest easy with this response.
| 2. Complementarity.
Sometimes the standard treatments try to go further and assure us
that all is well with things just the way they are. There is talk of
the necessity of using classical language to describe quantum
occurrences. And we are told that different measurements on
complementary quantities cannot be made simultaneously because the
apparatus for measuring one precludes setting up the apparatus for
the other. We then descend into a darkness where we are teased by
dim lights with names like "complementarity" that are so distant as
to remain obscure. These ideas derive from the writings of Niels Bohr, Einstein's adversary in the great debates over the foundations of quantum theory from its early years. For more see, "Einstein on the Completeness of Quantum Theory." |
 http://commons.wikimedia.org/wiki/File:Two_silhouette_profile_or_a_white_vase.jpg http://commons.wikimedia.org/wiki/File:Two_silhouette_profile_or_a_white_vase.jpg |
The consistent histories
approach is a development of this complementarity tradition. According to
it, there is no distinct process of measurement collapse. Rather there are
different frames in which fully consistent, probabilistic accounts can be
given of the aspects of the systems belonging to them. In the case of
Schroedinger's cat, there is a frame in which a superposition of live and
dead cat state can be found. However the frame does not allow us to
ascribe definite states of living or dead to the cat. That requires us to
move to different incompatible frames.
For more, see https://plato.stanford.edu/entries/qm-consistent-histories/#SchCat
3. Hidden variable theory.
In this response, we are told that the probabilities of quantum theory are
(as Einstein wanted) merely expressions of our ignorance. The best known
and best elaborated of these approaches is the de Broglie-Bohm pilot wave
theory. In it, in addition to its quantum wave, the particle also has a
definite position at all times. We just do not know that position. The
wave guides or pilots the motion of the particle, represented by changes
in this position property. The probabilities of measuring different
positions result from ignorance of the definite value of the position, not
from its lacking a definite value. While the theory gives an elegant
treatment of the simplest case of non-relativistic quantum mechanics, it
is strained to accommodate the later forms of quantum theory that emerged
in the decades following the 1920s.
| Quantum waves in a two slit experiment |
 Possible trajectories of particles in the two slit experiment according to the pilot wave theory. Only one of them is the true trajectory. http://commons.wikimedia.org/wiki/File:Doppelspalt.svg |
4. New dynamics.
In this approach, we suppose that the laws governing matter change when we
move from considering just a few particles to the very many that comprise
macroscopic bodies. It turns out that only very slight changes are needed
to eradicate the measurement problem completely and to give macroscopic
bodies properties that are very different from their microscopic
constituents.
The best known of these is the Ghirardi–Rimini–Weber theory, or "GRW." In
it, a quantum system will spontaneously undergo wave collapse purely of
its own accord, without any need to engage in the mysterious measurement
interaction. The probability of this collapse for a single quantum
particle is very small, so we do not notice the process on the atomic
scale. However, once we assemble many particles, then all it takes is for
just one to collapse. That then triggers collapse among the remaining
particles. While it is unlikely that any specific particle in a
macroscopic body will collapse, it is very likely that one of the very
many in the body will collapse. Thus, macroscopic bodies, consisting of
very many particles, are extremely unlikely to persist in superpositions.
They are almost certainly always in their collapsed states.
The principal difficulty with this approach is that no one is able to say just which of the many possible slight changes is the correct one.
5. No collapse theories, "many
worlds."
These theories propose that Schroedinger evolution is perfectly admissible
for both macroscopic and microscopic bodies. It denies that wave packet
collapse is a real process like Schroedinger evolution. The most popular
version of this approach employs the notion that all results of a
measurement are realized. When we see a radioactive atom decay at a
definite moment, we ourselves are really in a superposition of observers,
each observing a different time of decay. This is sometimes described
figuratively as if we are split into many observers who inhabit many
parallel worlds, all equally real.

This view describes the Schroedinger cat experiment as a process in which an observer, initially observing a live cat, splits into a superposition of observers, one that ends up observing a live cat and one that ends up observing a dead cat.
This simple splitting of the world is just one of a huge number of splittings that are happening all the time. The world of our common experience turns out to be one slender branch in an immense and ever-growing tree-like structure in which the world is splitting into branches and splitting again and splitting again, and so on inexorably for ever.
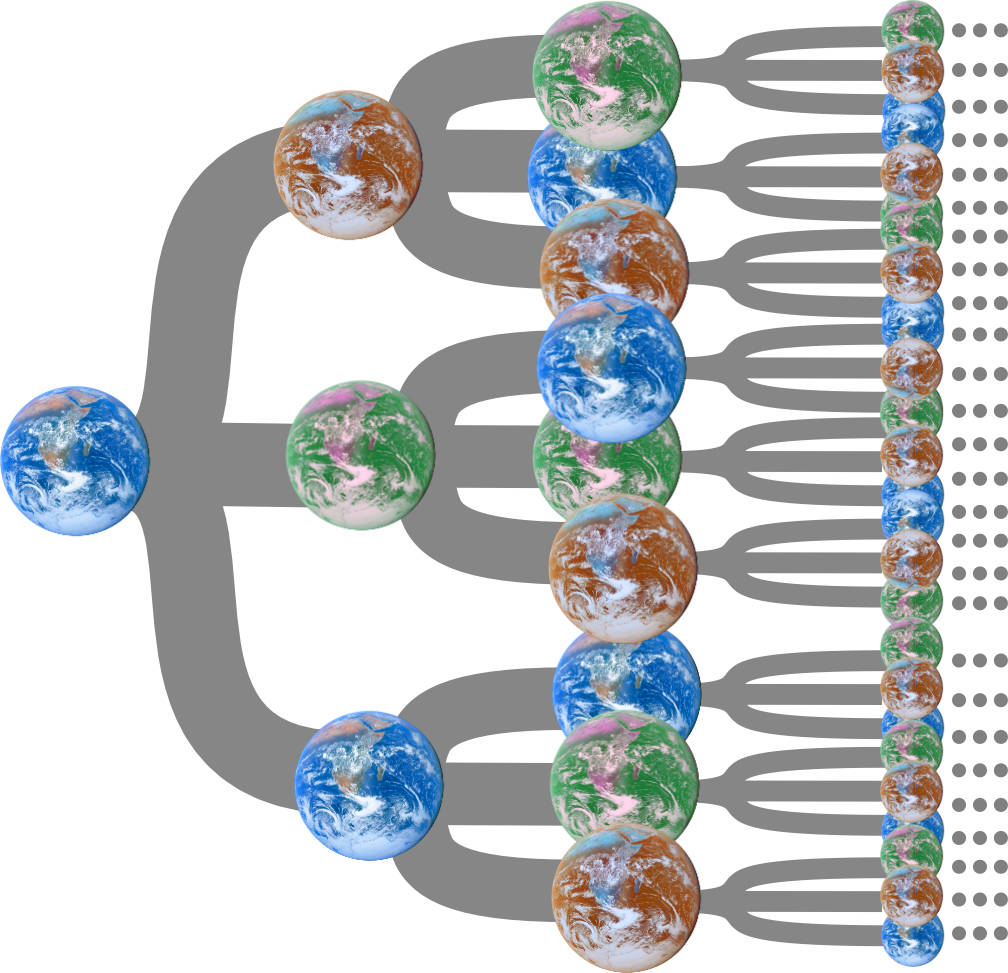
This approach requires some dedication. We must be quite committed to the idea that a theory devised for tiny particles applies unchanged to macroscopic bodies. For it requires us to give up the most fundamental aspect of our laboratory experience, that experiments have single, definite results.
There are still further accounts
whose complications cannot easily be developed here. "Decoherence" is a
process in which a quantum particle becomes entangled with the many
particles of a much larger environment. There was, for a while, some hope
that the details of the physics of this entanglement alone might be enough
to explain how the particle wave collapses on measurement.
More extreme accounts try to resolve the problem by changing quite basic
ideas of ordinary science. One idea is that quantum systems conform to a
different logic--"quantum logic." Another is
that the information held in quantum systems is of a different type from
that in ordinary classical systems. These differences are investigated in
the study of "quantum information." While
interesting ideas have come from all these investigations, they have yet
to provide a clear solution to the measurement problem, in spite of hopes
that they might.
My own feeling is that none of
these responses is satisfactory. The least defective is the fourth.
However, if there are new physical laws that would resolve the measurement
problem, we can be pretty sure that they are quite exotic and not produced
by a small adjustment in our existing theories. For, if these small
adjustments are there to be found, eight decades of work by many of the
brightest minds in quantum physics has failed to find them.
Nonetheless, this "new, as yet unknown, physics" response is the one that
all the other responses have to beat. Ask each of them, is this response
more plausible than the "new physics" response? In each case, I answer no.
Copyright John D. Norton. April 2001; March 16, August 22, December 1, 2008; March 7, 2010; April 13, 2015. Minor addition, July 31, 2020. February 6, April 19, 2022. April 16, 2024.