
| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
In past chapters we have seen how unusual spacetimes can permit time travelers to travel back in time and visit their past and their ancestors. We have also seen how quantum mechanics opens the possibility of superpositions of incompatible states. We have seen cats that are both alive and dead at the same time. This chapter explores a way that both of these oddities can be combined into a single problem. It's "time travels with Schrödinger's cat."
Let us recall briefly the grandfather paradox from an earlier chapter. A time traveler goes back in time and kills his own grandfather. A contradiction ensues. For if the grandfather is killed; the grandson is never born; there is no time traveler and the grandfather is not killed.

The earlier chapter outlined what seemed to be the only possible solution. Since a successful assassination leads to a contradiction and contradictory situations are impossible, the assassination cannot succeed. The assassin must fail.
Here we will see if there is a way to make sense of what would happen in a universe in which the grandson assassin succeeds.
The standard form of the grandfather paradox is both macabre and ill-suited to the sort of analysis that will follow. In its place, we will proceed with a benevolent version of the grandfather paradox. Instead of the time traveling grandson trying to kill the grandfather, he seeks to convince him to undertake a life of celibacy, devoted to good works of charity benefiting all people.
A paradox will still ensue if we assume that the grandson succeeds in his persuasion. For if the grandfather adopts a life of celibacy, he will have no children and no grandchildren. There will no time traveler and thus no one to persuade him to adopt a life of celibacy. As before we have:
| Time traveler goes back in time. |  |
Grandfather adopts a life of celibacy. |  |
Time traveler does not go back in time. | |
| Time traveler does not go back in time. |  |
Grandfather does not adopt a life of celibacy. |  |
Time traveler goes back in time. |
Once again, it seems that the only escape from the paradox is conclude that the time traveling grandson must fail to convince the grandfather to adopt a life of celibate benevolence.
This escape is based on a presumption that one would normally never think to challenge:
At any one time, only one thing can happen.
That is, at the time of their meeting, the grandfather either adopts a life of celibacy or a life of procreation. He can do only one of these. And the only one that leads to overall consistency is that he adopts a life of procreation. Then his time traveling grandson can appear, but the time traveling grandson must fail to convince him to adopt celibacy. For only one thing can happen; and that failure has already happened.
Quantum mechanics leads us to think of things that are not normal. The problem of Schrödinger's cat leads us to entertain seriously that a cat can evolve into a single state in which it is both alive and dead. The state is a superposition of the live and dead states.
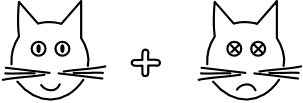
The notion of a superposition is a technical notion in quantum mechanics. In the theory, the states of the cat form a vector space, something like the space of directions mapped out by a compass. Typical directions include NORTH and EAST. We find nothing remarkable in forming a sum--a superposition--of the two:
NORTHEAST = NORTH + EAST
It is equal parts NORTH and EAST.
The superposition of live and dead states is, in quantum terms, no more remarkable. We can add the states to produce a superposition. We will write it as:
| cat > = | live > + | dead >
The "-ket" notation "| something >" was introduced by a founding figure of modern quantum theory, Paul Dirac. It tells us that the "something" state is a vector in the sort of vector space employed by quantum theory.
Let us treat the states in the benevolent grandfather paradox as quantum states. We hope the paradox will be resolved, so we will not call it a paradox but a process. We will consider two possible states at the time that the time traveling grandson meets his grandfather:
| celibate > = the grandfather is convinced to adopt a life of benevolent celibacy
| procreative > = the grandfather lives an ordinary life in which he has children and grandchildren.
We will assume the interesting case in which the time traveling grandson convinces his grandfather to adopt a celibate life. In this case, a contradiction arises in the non-quantum case since each of these states evolves in time into the other.
Let us try to implement these states in a time travel universe. We will consider the "cylinder universe" described earlier. In it, one can travel in time merely by living long enough. Eventually, someone who lives long enough will completely traverse all time and end up at their starting event.
For the implementation of the quantum benevolent grandfather process to succeed in this universe, we assume that the time traveling grandson survives long enough to meet his grandfather.
If we treat the two states individually, the paradox remains. The initial state "| procreative >" evolves through time to become "| celibate >". For the arrival of the grandson leads the grandfather to adopt a life of celibacy.
(1) | procreative > -----> | celibate >
However that evolved state | celibate > fails to match the initializing state | procreative >.
Correspondingly, if we start with the initial state "| celibate >", it will evolve in time to become | procreative >. For now there is no time traveling grandson to lead the grandfather to a life of celibacy.
(2) | celibate > -----> | procreative >
Once again the evolved state fails to match its initializing state.
If these were the ordinary states of classical physics, we would be trapped in a contradiction. However since these are by supposition quantum states, we can form a superposition:
| procreative > + | celibate >
How will this superposition evolve in time? Under the natural assumption that the essential physics of the time evolution is captured by the simple green-red oscillator model below, this superposition can evolve in time back to itself.
(3) | procreative > + | celibate > -----> | procreative > + | celibate >
The linearity of quantum theory allows us to pass from time evolutions (1) and (2) to (3) merely by "adding them up." The linearity of the theory permits us to form new states by adding them together. That same linearity permits us to add their time evolutions as well. There is a complication however that means that we need several steps to complete the adding up. For those who are interested in the details, they are described below in the section "How to Add Up the Evolutions in Time of the Benevolent Grandfather Process."
We now have a consistent physics in which the present state | procreative > + | celibate > evolves in time to a state that matches its initial state after it travels through all of time to return to the initialing moment.
Fussy details, for those who want them.
There is complication in adding up the time evolutions (1) and (2) to arrive at (3). The complication is that the two evolutions (1) and (2) will, in general, take different amounts of time. (We can see this effect is the simplified example of green and red lights below.) If the processes start at the same time, their end states will arise at different times. That means that the end states cannot be summed to give a single end state at one time.
The problem is resolved by paying a little more attention to the timing. Let us say that time evolutions (1) and (2) need times σ and τ, respectively, where σ + τ are, in general, unequal. We will write this as:
| procreative > --- σ ---> | celibate
>
| celibate > ------ τ ---> | procreative >
Since the first process ends in the start state of the second; and the second process ends in the start state of the first, we can extend each with the subsequent steps to recover:
| procreative > --- σ ---> | celibate >
------ τ ---> | procreative >
| celibate > ------ τ ---> | procreative >
--- σ ---> | celibate >
In each of these two extended processes, the intermediate states arise at different times. For the first, the intermediate state | celibate > arises after time σ. For the second process, the intermediate state | procreative > arises after a different time τ. However the end states of both processes arise at the same time
σ + τ = τ + σ
We can simplify our description of these two extended processes by omitting mention of the intermediate states. We have two processes that take the same time σ + τ:
| procreative > --- σ + τ ---> | procreative
>
| celibate > -------- τ + σ ---> | celibate >
Since they take the same time, the linearity of quantum theory does allow us to add them up. We then get the result (3) sought:
| procreative > + | celibate > --- σ + τ ---> | procreative > + | celibate >
A weakness of this last analysis is that the systems involved are extremely complicated. We are tracking the evolution in time of human beings in human environments. How exactly are we to imagine that the totality of the human society presumed can be wrapped around a cylinder universe so that its evolved state matches its initial state? Might there be some sticking point in the analysis that we overlook simply because these systems are too complicated to fully comprehend?
A standard way to alleviate this concern is to devise a "toy model" whose physics is fully comprehensible, but which still manifests the effect of interest. I will describe such a model here.
The model is a very simple quantum system that has just two states. We will picture them as lights. The system in state | green > lights as a green light; and the system in state | red > lights as a red light. Superpositions of these states are possible (and essential for what is to follow).
We can define a simple dynamics in which the system oscillates between the two states | green > and | red >. This is achieved by supposing that the two states interact as follows:
| green > "on" tends to suppress | red >
| red > "on" tends to suppress | green >
If we set up these suppression processes appropriately, the system will oscillate indefinitely between the two states | green > and | red >.
In the analysis in the linked document (for experts!), A Simple Quantum Mechanical Oscillator, it turns out that the time period needed for this oscillation to complete depends upon the energy associated with the interaction. The greater the energy, the smaller the period and the faster the oscillations. (Generating Word doc linked here.)
If you care to see it, there is a simple relationship that connects the period "T" of oscillation and the energy:
T = h / energy
where h is just Planck's constant of quantum theory.
There is a simple way to visualize the states and also the dynamics of the oscillator. The two states | green > and | red > form a vector space, something like the vector space of directions formed by NORTH and EAST.
The superposition | green > + | red > occupies the intermediate position corresponding to Northeast.
| The dynamics simply consists of the vector state
rotating uniformly through all quadrants of the vector
space. To picture this, imagine that the compass needle in the space of directions simply rotates uniformly from East --> North --> West --> etc. The analogous rotation in the red-green vector space is the evolution of the two state quantum system over its states. A full cycle will require time T above. |
This picture properly portrays a
quantum complication. The state will evolve from | green > to - | green > (read "minus | green >") in the time half T. For external purposes this minus state is indistinguishable from the original | green > state. However, internally, in terms of the relations to the | red > state, the minus matters. We need the full cycle time of T to eliminate it and to restore the system to its original state. We can also see from the figure that the oscillator will required time T/4--a quarter turn--to evolve from | green > to | red >. However it will need a longer time of 3T/4 to evolve from | red > back to | green >. A quarter turn of just T/4 is not enough. It takes |red> only to -|green>. |
To employ this system in our efforts to address the time travel paradox, we need first to find a time travel cylinder universe tuned to the dynamics of the two state quantum system. Each cylinder universe will have a recurrence time, the time that elapses for a being in the universe while completing one full cycle and returning to its initial state. The tuning requires that this recurrence time match exactly the time of process of interest. Those times will differ from case to case and thus require different universes. The process times considered below are: time for | green > to evolve to | red >, time for | red > to evolve to | green > and finally the time T for the superposition to evolve back to itself. With that match achieved, we can explore which initial conditions will yield non-contradictory time evolutions in the time travel universe.
If the initial state is | green >, the oscillator evolves to | red > in completing one cycle of time in the cylinder universe. We have a failure of the evolved state to match the initial state.
If the initial state is | red >, the oscillator evolves to | green > in completing one cycle of time in the cylinder universe. We have a failure of the evolved state to match the initial state.
However, if the initial state is the superposition | green > + | red >, then over time T the initial state evolves back into itself. The evolved state matches its initial state. We have a consistent time evolution with the time travel universe.
Paradox resolved!
Paradox resolved? Or is it? Below I sketch problems whose import is that we have gained little, but have raised a host more of problems
1. Global Constraints Persist
Recall the original problem. We chafed under the imposition of global constraints. They meant that the assassinating grandson must fail; or the pleading grandson of the benevolent version of the paradox must fail. Yet the reasons for the failures are invisible locally. We can only understand them by recalling the global circumstances of the time travel.
We will have that same problem. The time to traverse the cylinder universe must match exactly the period of oscillation of the two state oscillator. The slightest mismatch of the two times and the evolved state will no longer coincide with the initial state. Yet there will be no reason visible locally for why we must have an oscillator whose period matches some constant value with no local meaning.
To get a sense of how awkward that is, imagine that we have two oscillators side by side. The period T of the first, we suppose, matches the cosmic recurrence time. A very slight variation in the manufacture of the second oscillator, we now suppose, means that its recurrence time is 1% longer, that is, 1.01T. After time T, the first oscillator will have evolved to match its original state as it completes one cosmic cycle. The second however will not have completely returned to its original state. We will have a contradictory mismatch of the initial and evolved state of the second oscillator. The slightest mismatch of oscillator period and cosmic recurrence time is fatal to the quantum resolution, which now fails.
We are still in the malign grip of global constraints.
2. Most Quantum Systems are not Exactly Periodic in Time
The green-red oscillator is a simple quantum system whose state recurs exactly with period T. This exact recurrence is exceptional. Most quantum systems of any complexity might come arbitrarily close to recurrence if we wait a very, very long time. However most will never return exactly to their original states. Hence most superpositions cannot be used in the resolution of the paradoxes proposed.
To get a sense of how this comes about, consider the two oscillators above with periods T and 1.01T. If we find a universe with recurrence time 101T, then the pair of oscillators will return to their original states in completing once cosmic cycle.
• The first oscillator with period T will complete 101T/T
= 101 of its cycles.
• The second oscillator with period 1.01T will complete 101T/1.01T = 100
of its cycles.
It might seem, then, that just waiting long enough will always secure exact periodicity. That is not so. This last case is special. T and 1.01T are rational multiples of each other: 100:101. If the ratio of periods were irrational, then, no matter how long we wait, exact periodicity would never arise.
(For experts.) These last considerations are close to those that apply quite generally to the recurrence of quantum system. If a system is in an energy eigenstate with energy E, then it evolves with a unitary time evolution operator U(t) = exp(iEt/ℏ). This system will recur after Et/ℏ = 2π, that is, t = h/E. Generic systems will be in a superposition of energy eigenstates, with energies E1, E2, E3, ... Each will cycle with a period t1 = h/E1, t2 = h/E2, t3 = h/E3, ... Exact recurrence of the superposition can only come about if all these periods are rational multiples of one another. That is a circumstance that will not arise generically. It will appear only in highly contrived special cases.
The benevolent grandfather process has been set up above to be one of the exceptional cases that are exactly periodic in time. That it is periodic is enforced by the assumptions of the time evolution (1) and (2). If we chain them together, we see that, over time, each of the states | procreative > and | celibate > evolve back into themselves exactly.
It is easy to see that this exact periodicity is exceptional even among benevolent grandfather processes. To see why, imagine that there are many variant ways, differing only in tiny details, that a grandfather can be in the procreative state and the celibate state. Call them
| procreative1 >, | procreative2
>, | procreative3 >, ...
| celibate1 >, | celibate2 >, | celibate3
>, ...
Then we implement the essential narrative for the benevolent grandfather process if we have time evolutions:
| procreative1 > -----> | celibate1 > -----> | procreative2 > -----> | celibate2 > -----> ...
However this evolution will not in general admit any periodicity.
There will be exceptional cases in which periodicity is recoverable. I believe that such periodicity can arise only if eventually one of the states repeats. For example, periodicity is restored if, say, | procreative1 > = | procreative100 >.
3. Why Can We Replace a Macroscopic Contradiction with a Quantum Superposition?
The quantum solution to the time travel paradoxes depends on a supposition: that the contradiction of a grandfather in two incompatible states can be replaced by a quantum superposition of these two states.
Quantum theory is a physical theory whose laws tell us when superpositions arise. The do so often at the atomic scale. A particle momentarily localized in space rapidly evolves to a state that is a superposition of many positions. That is just the evolution of the particle under the Schrödinger equation.
Now we have a time traveling grandson seeking to convince his grandfather to adopt a life of celibacy. As far as we know, the grandfather may adopt one of the two courses. What specifically in the laws of quantum theory tells us that this particular interaction is somehow to be associated with a superposition? The interaction is macroscopic and, it would seem, covered by non-quantum physics. There is nothing specifically quantum mechanical about these two possibilities that would require us to represent the two possibilities as a quantum superposition.
To sharpen the last worry, imagine that the grandfather
and son are not human systems but intricate
mechanical robots, governed by ordinary Newtonian mechanics. Then
there is nothing in the interaction of the robotic grandfather and the
robotic son that would call for quantum superpositions.
4. Are there Macroscopic Quantum Superpositions?
Of course all these systems are ultimately quantum systems in the sense that they are composed of atoms and the like. However we have to suppose that the peculiar linear superpositions of quantum scales persists without the slightest alteration when we deal with macroscopic systems. That is, we have to assume that there really is a superposition of dead and alive cat in Schrödinger's famous thought experiment. To accept this possibility, we have to explain away why it is that we macroscopic humans do not see these superpositions at the macroscopic scale. Were we to do the macabre experiment, we would open the box to find either a live cat or a dead cat. If one imagines that our observing the cat is sufficient to collapse the superposition, then the same must happen to the grandfather superposition when someone happens to glance at it. That glance would destroy the quantum resolution of the paradox.
5. What is it to Experience a Superposition?
Set these last two worries aside. Without them we still have to make assumptions about what it is like to be in a superposition. In the narrative, the grandfather is in both the procreative and celibate states. We might just accept that, if he adopts this intermediate state, he would know it. He would sense that he is somehow both and neither at the same time. Analogously, if our course in space is Northeast, we know that it is neither purely North nor East but something that has elements of both.
If this conception is unappealing, we might ask for some account of a superposition in which each component of the superposed grandfather state would be unaware of the other component. Such an account is offered by the Everett "many worlds" interpretation of quantum theory through the process of decoherence. This account remains under debate in the philosophy of physics community. I side with the skeptics. If we accept the account, however, we find that it still provides little comfort for the resolution of the time travel paradoxes. We saw above that the quantum resolution can only succeed with systems that are exactly periodic. This interpretation makes it even harder to secure such systems. The decoherence mechanism that isolates the components of a superposition disrupts the periodicity of even the simple green-red oscillator.
(For the more expert.) The issues are technically messy, so they are relegated here to smaller type. In the Everett "many worlds" interpretation, each component of the superposition becomes entangled quantum mechanically with the many degrees of freedom of the environment. The procreative grandfather becomes entangled with his environment. The celibate grandfather becomes entangled with his environment. The key fact is that these two environments are almost completely disjoint from one another. The outcome is that each component of the grandfather superposition evolves "for all practical purpose," that is "very nearly enough," as if it were independent of the other component.
If we now assume that the consciousness of the grandfather is fully fixed by his physical state, it is plausible that whatever slight residual entanglement one component has with the other becomes invisible to the consciousness of the component. That is, one component grandfather is not conscious of the other and so experiences the superposition state as if it were just one of the components in isolation.
Recurrence is now all but impossible to secure for all practical purposes. This happens even in the simple case of the green-red oscillator. Once we assume that the component green or red states of the superposition become entangled with their environments, they no longer revert to their initial superposition after the time period T. Instead the best we can hope for is recurrence in the combined system of oscillator and its hugely complicated environment. For reasons given in 2. above, this rarely happens.
(Proponents of the Everett interpretation will have to forgive me for interjecting a note of incredulity. Our goal is to provide an understanding of the quantum character of the world. It is a fundamental physical theory grounded in the behavior of atoms, particles and radiation. We now find that, to ensure the viability of this particular interpretation of the theory, we have to venture into speculation about our consciousness. We must do that in human systems that are at a scale many orders of magnitude larger than those in which quantum theory was established. Worse, we have to find reasons in those ventures for why the vast majority of all that exists is invisible to our consciousness. What is invisible are not benign things like atoms too small to see or radio waves outside the visible spectrum. The invisible existents are duplicates of ourselves, all the people and objects around us, the buildings that house them, the buses, trains, and planes we travel in, moons, planets, stars, galaxies, and so on; and all that in an unimaginably complicated myriad of variant forms. What requires all these existents is not the quite reasonable assumption that quantum theory applies to macroscopic systems in some good approximation. It is that a particular feature of quantum theory, its linearity, persists for all interactions without the slightest modification as we migrate from atomic to macroscopic scales.)
The idea the quantum mechanics can alleviate the paradoxes of time travel is best known from work by David Deutsch. See: David Deutsch and Michael Lockwood, "The Quantum Physics of Time Travel," Scientific American, March 1994, pp. 68-74.
Their construction involves a worm hole. That is, instead of wrapping the totality of spacetime back onto itself, the traveler falls into a hole in spacetime that wraps back in time to deliver the traveler at an earlier time. This construction raises many more technical issues than the simpler construction used above.
With the wormhole construction we are left uncertain of just what the character of space and time is around the tears. How do they come about? How does matter behave in their vicinity?
With the simpler construction used here of the cylinder universe, these issues do not arise. We simply take the physics of an ordinary Minkowski spacetime of special relativity and wrap it up.
Deutsch's proposal has been subject to telling criticism by Frank Arntzenius and Tim Maudlin. See Section 9 of:
Arntzenius, Frank and Maudlin, Tim, "Time Travel and Modern Physics", The Stanford Encyclopedia of Philosophy (Winter 2013 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/win2013/entries/time-travel-phys/>.
More recently, Seth Lloyd and his collaborators have devised a variation that employs quantum teleportation. See Seth Lloyd et al., "The quantum mechanics of time travel through post-selected teleportation," https://arxiv.org/abs/1007.2615 Their exposition is quite technical and forbidding to non-experts.
Copyright John D. Norton. September 3, 5, 7, 2018.