| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
| Before we turn to pursue the spacetime that best resembles our own in the next chapter, it is interesting to review how Einstein's theory allows us to describe universes in which time travel is possible. | The analysis of this chapter is classical in the sense of being relativistic, but not quantum. Are you wondering what would happen if we add quantum mechanics to time travel? Then look at the later chapter "Time Travels with Schrödinger's Cat." |
The easiest type of time travel universe looks like a trick that is stipulated into existence. However there is nothing illicit about it. And its great simplicity enables us to refine our intuitions about just how time travel can arise.
Einstein showed us through the Einstein universe that we can curve space back onto itself and thus produce a closed space.
That construction proved a little complicated for Einstein since there are three dimensions of space that need to be accommodated. If we want to do it in the time direction, it is much easier. There is only one dimension of time. The simplest case arises if we wrap up the time direction of a Minkowski spacetime. As before, if we consider only one dimension of space, we recover a cylinder. The spacetime is on the surface of the cylinder. For the new case the cylinder is wrapped up in the timelike direction.
|
You might wonder if a trick like this is really allowed by Einstein's gravitational field equations. It is. Recall that Einstein's gravitational field equations merely fix how each little patch of spacetime must look. A solution is admissible if each patch connects properly with those next to it. That will happen in this spacetime. In any not too big piece, this cylinder universe is exactly the same as our original Minkowski spacetime; each piece connects with the one next to it just as they do in a Minkowski spacetime. That is all that is needed for the spacetime to count as a solution of Einstein's gravitational field equations. It is only when we look at the spacetime as a whole that we see that the spacetime is no longer the same as our original Minkowski spacetime. |
The timelike curve on the spacetime represents the life of a traveler who stays at one point in space, but passes through time merely by being. Eventually that worldline will wrap all the way around the spacetime and reconnect. At that point, the traveler will meet his or her former self.
| The simple picture of a cylinder above suppresses the full, four dimensional structure of the spacetime. We can describe what is missing, but it is very hard to visualize. Each horizontal line in the cylinder actually represents an infinite, three-dimensional Euclidean space, which is the same as the ordinary Euclidean space of our original Minkowski spacetime at one instant of time. The figure on the right adds in one extra dimension of space for such a line to give some indication of what has been omitted. However there is much more that is not shown. The two-dimensional space indicated is actually infinite in both its spatial directions; and the third, infinite dimension of space is not shown at all. |
The traditional "grandfather" paradox of time travel arises if the latest stage of the traveler (now imagined to be the grandson of the original traveler) were to kill the original one (the grandfather). A contradiction would ensue. With the assassination complete, there would be no traveler to pass through time and commit it. So the assassination happening entails that it doesn't happen.
We have already discussed the difficulties raised by such a paradox in the discussion of tachyons earlier. The difficulty is that we would visit a logical contradiction on our physical theory and that is unsustainable in any cogent physical theory.
| Time traveler goes back in time. |  |
Time traveler kills grandfather |  |
Time traveler does not go back in time. | |
| Time traveler does not go back in time. |  |
Time traveler does not kill grandfather |  |
Time traveler goes back in time. |
So we have a contradiction:
| Time traveler goes back in time. | if
and only if |
Time traveler does not go back in time. |
Contradictions may be fine in science fiction or when we are writing a screen play for a time travel movie. However contradictions are a mortal threat to a physical theory. From time to time, we will work with an inconsistent theory. We shall see that this happened in the early years of quantum theory. However this tolerance has to be temporary. For an inconsistent theory cannot reliably tell you what is the case. It assures you that some assertion is both true and false at the same time.
The possibility of such paradoxes has led some to conclude that time travel universes are logical impossibilities. That is too hasty. There is an obvious loophole in the paradox. If the assassination attempt fails, then there is no contradiction.
So that is what must happen in a time travel universe. The grandson's bullet must miss; or the gun misfire; or the grandfather ducks; or who knows what. For if the assassination attempt didn't fail, there would be no assassin to attempt it.
To put it another way, when the grandson arrives to assassinate his grandfather, the failure of the assassination has already happened in the grandson's past. It has already happened and so cannot be undone by whatever the grandson may try to do.

That resolution is, as far as I know, admissible. Many find it objectionable since there seems to be no reason in the physics itself that forces the failure of the assassination attempt. What if the grandson takes all due care, aims carefully with a new gun, and so on? How can we be so sure that the attempt will fail.
We can. The intuitions that tell us it will not fail are honed in a type of universe that is quite different from a time travel universe. In the ordinary time travel free universes, such as we presume we inhabit, local constraints prevail. If the gun misfired, for example, it was because something in the state of the gun immediately prior to to the assassination attempt intervened. Perhaps the grandson passed through a rain shower and a component of the gun began to rust.
In a time travel universe, in addition to these sorts of local constraints, we have a new type: global constraints. These are extra constraints to which all processes must conform in order that distant future and distant past mesh when they meet. These global constraints do not arise in time-travel-free universes. They are what assures us that the assassination attempt must fail.
We can get an idea of how they work from the jigsaw puzzle analogy for solving Einstein's equations.
| First consider a universe without time travel. We
start with a row of pieces that represents space in the present
instant. Then we add successive rows that correspond with space in
successive future times. The pieces we add are constrained
only by the local requirement that each piece mesh with
those immediately before and after it in time; and those around it
in space. These pieces specify the local condition of spacetime: the curvature of its geometry and its matter content. So one piece will have a grandfather; and the successive pieces fitted to it will have the grandfather engendering children, aging and so on. There will also be pieces in which assassins shoot their victims. |
| Now take the case of a time travel universe. All
these constraints apply. But, in addition, as we keep adding the
successive rows, we will eventually end up going all the way round
the space and then the new and powerful constraint will come into
force. The last row we add has to be so perfectly built that it
meshes with the past edge of the first row we put in place. That is
a global constraint. It means that in our planning of which pieces
to lay down, we had to worry about the local meshing of the pieces;
and, in addition, we had to select pieces now so that eventually the
final meshing of last and first row
would work out. If that last piece that we add contains the time traveler attempting to assassinate his grandfather, then that piece must mesh with the past. Those past pieces would contain the time traveler loading his gun and walking down the street to the house of his grandfather. It must also mesh with the future pieces. Those future pieces will contain a live grandfather who survives, for those pieces will in turn develop forward to give us the time traveler. That meshing with the future pieces can only happen if the time traveler fails in the assassination attempt. |
Here's a simple example in a different arena of how these
sorts of global constraints can work. It is the arithmetic
puzzle, "99." In the puzzle, you are to start at zero and may add
or subtract any number you like between 0 and 10, as many times as you
like, provided that the numbers that you are adding or subtracting are
always even numbers. Is there some combination of additions and
subtractions that will get you to 99?
Locally, there is no obstacle to getting to
99. If you could somehow get your sum to 97 or to 95, you could complete
the task by adding 2 or 4. Just looking locally at the numbers around 99
reveals no problems.
..., 87, 95, 91, 97, 99.
Globally, however, there is a constraint that
necessarily defeats your attempts to arrive at 99. Since you start with
zero and may add or subtract even numbers only, your sum must always be an
even number. So you can never get to 97 or 95 or any other number that is
an even number removed from 99. This global constraint assures your
failure to solve the puzzle.
0, 8, 4, 12, 16, 24, 22, 30, ...
That is how things would work also for the time-traveling would-be assassin. The assassin can get to states very close to the successful assassination--the "99" of the puzzle. However those close states would always be the even states, "94," "96", "98," ... They look close to the assassination sought, but physical laws preclude them developing into the successful assassination.
Another simple illustration shows just how powerful these global restriction on a spacetime can be. Consider just about the simplest possible time travel universe: a universe empty of all matter excepting just one mass. Now pick some time slice. What configurations of the particle are possible?
In an ordinary time-travel free universe, at some initial moment of time, we can have the worldline of the mass with any initial velocity.
If the spacetime is a time-travel, cylinder universe, we are strangely restricted in the possibilities for this time slice. We could choose a mass at rest. That corresponds to the case of a single worldline that eventually wraps back onto itself. But if we have the mass initially moving, then we must also stipulate that clone masses be distributed in space at uniform intervals. These will be the repeated returns of the single mass as it travels all the way round spacetime and back to the present.
The global constraint says that if we have a moving mass here and now, we must also have a moving mass there and now; and there and now; and so on. That sort of constraint would be incomprehensible in a universe without time travel. What reason of physics, we would exclaim, requires it--just as we ask, what reason of physics requires the grandson's assassination attempt to fail!
The cylindrical Minkowski spacetime described above is a spacetime admitted by Einstein's general theory of relativity. It is possible to feel a little discomfort at the way that time travel was introduced. Because the spacetime is, in all its parts, just like an ordinary Minkowski spacetime of special relativity, the wrapping up that produces time travel can seem contrived. There is no reason to be found, we might say, in any of the parts for why something odd should happen.
| This example has been explored in some detail in my "A Simple Minkowskian Time-Travel Spacetime." | It might be nice if we could point to some specific pathology in the spacetime that we could blame for the possibility of time travel. Here is one of the simplest ways to modify a Minkowski spacetime with a pathology, so that time travel is possible, yet the spacetime remains in all its parts but one just like the ordinary spacetime of special relativity. The difference is the presence of a single pathology, a "conical singularity," whose nature will be explained shortly. The overall structure of the spacetime is shown in the figure below. The figure below suppresses two dimensions of space and shows only one dimension of space and one of time. |
On the left of the figure, the spacetime is like a familiar Minkowski spacetime. The timelike direction is horizontal in the figure. The pathology is on the right where we find the conical singularity. The trajectories shown are timelike geodesics, that is, the worldlines of bodies in inertial states of motion. They can be instantiated by bodies to which no forces are applied, so that they do not accelerate. An example would be a spaceship that has turned off its rocket motors and is just lying idle in space.
On the right of the figure above, in the vicinity of the conical singularity, the timelike geodesics, which approach from the left of the figure, are diverted and returned to the left of the figure. The effect is that a traveler, whose wordline is one of these geodesics, will return to part of the spacetime in the traveler's past. The traveler does not have to do anything special for the return to happen. An idling spaceship just has to sit and wait. Merely persisting in time is enough. Such travelers will eventually come to a part of the spacetime in which their timelike geodesics are directed into the past. Such travelers will encounter their former selves and may, for example, exchange light signals with their former selves.
If we consider travelers that are accelerated, they may even collide with thier past selves, as shown below. (To maintain consistency and avoid "grandfather" type paradoxes,, we assume that the collision is a "near miss" that does not destroy the older version of the time traveler.)
| A note on terminology: time-travel universes are commonly described as those that harbor "closed timelike curves." An example is the worldline of a single mass in a cylinder universe, shown at right. The distinctive property is that the mass traverses the entirety of the worldline, repeatedly, without ever coming to and end and without ever having to reverse its direction in time. The self-intersecting worldline of the traveler in the universe with a conical singularity is not like this. At the intersection with the past self, the traveler cannot continue in the loop without reversing its direction in time. That is, its trajectory is not a closed timelike curve. |
What makes this time travel universe even stranger than the cylinder universe is that it is not time orientable. That is, elsewhere, in the cylinder universe and many others, it is always possible to designate which is the future light cone and which is the past light cone, such that there is a uniform sense over the whole spacetime of which direction in time is the future and which is the past. It is evident from the figure that this is no longer possible in his new spacetime. The traveler and the traveler's future returning self will disagree when they meet on which direction is the future and which is the past. This disagreement is shown by the conflicting directions of the arrows in the figure below, where the arrows attempt to indicate the future direction in time.
We come to the lingering question. Just what is a conical singularity? It is a class of singularities that gets its name from the simplest case. That case arises when we take a sheet of paper and cut out a wedge. The figure below shows a quarter of the sheet cut out. We then connect the edges to form a cone.
As long as we consider regions of the cone that do not include or enclose the apex, the geometry intrinsic to the surface is just the ordinary flat Euclidean geometry of original piece of paper. It takes no special insight to see that something has gone awry at the apex. Diagnosing exactly what has gone awry is a little complicated. We shall see in later chapters that singularities that commonly arise in general relativity have a different character. They are "curvature singularities." They signal their presence by a disturbance in the curvature of spacetime in their vicinity. That is, as we approach the singularity, we find the curvature of spacetime growing without limit. Physics in their vicinity becomes distorted by extreme gravitational effects.
A conical singularity is unlike these curvature singularities. The space of the conical surface remains quite ordinary, no matter how closely we come to the apex. It is only at the apex itself that there is pathology. One manifestation of the pathology is shown by circles that enclose the apex. The figure shows a circle centered on the apex with radius r. The construction shows that the circle does conform with the familiar Euclidean result that its circumference is 2π r. It is (3/4)2π r.
The conical singularity in the time-travel Minkowski spacetime is produced by essentially the same construction. We start with an ordinary Minkowski spacetime and excise one half as shown in the figure. We then connect the edges in the same way as we connected the edges of the paper to form a cone. The portion excised has to be carefully chosen so that the spacetime geometry remains regular at the join of the edges. Excising exactly half the spacetime as shown conforms with this requirement.
That's it. We now have the time-travel spacetime of this section. The conical singularity is at the apex, which is the event in spacetime that serves as the axis around which we connected the exposed edges of spacetime. Consider a timelike geodesic in the original, unexcised spacetime. After the excision and joining of the edges, this timelike geodesic becomes a curve that loops around the apex, which is where the conical singularity resides. It is this looping that gives us the time-travel behavior. As with the simple cone, all regions of the spacetime that do not enclose this singular apex remain ordinary and flat, just like a familiiar Minkowski spacetime. Since we have not disturbed the spacetime through which the timelike geodesic passes, the curve remains a timelike geodesic of the new spacetime.
In the case of the paper cone, the singular apex has the character of a point. It has two dimensions less that the two dimensions of the cone's surface. Similarly, the conical singularity in the Minkowski is not a point, but something like a two-dimensional surface that has two dimensions less than the four dimensions of the spacetime. We have to say "something like" since strictly speaking, the singularity itself is not a proper part of Minkowski spacetime. There is no way, for example, to ascribe a metrical structure to it that is consistent with the rest of the spacetime. (For more details, see my paper )
Finally, I must issue a disclaimer. I have suggested that this example of a time-travel universe is somehow more congenial since we can identify a cause for the pathological behavior. In my view, that it is more congenial is simply a matter of our psychological comfort. I resist any suggestion that this new spacetime now conforms the time-travel behavior with some prior requirement of causal order in the universe, such as might be demanded by a causal metaphysics. Such metaphysics, I have argued, can provide no factual restriction on the content of our physical theories. For a recent analysis, see my "The Metaphysics of Causation: An Empiricist Critique." in Yafeng Shen, ed., Alternative Approaches to Causation. Oxford University Press, forthcoming.
The cases of the cylinder universe and the spacetime with a conical singularity indicate that "cut and paste" techniques can easily deliver spacetimes in which time travel is possible. An example that is often mentioned in popular literature is a "wormhole." Such a structure can be constructed by cut and paste methods as follows.
In such a structure, two cuts are made in the spacetime so that the later one can be connected to one that is temporally earlier in some manner. The figure shows the connection implemented by adding a new portion of the spacetime. It might also be done just by attaching the appropriate exposed edges directly to each other. (That is hard to draw, so I have not tried.) Then a traveler can enter the first region at the later cut and reappear earlier in time at the earlier cut.
The sorts of time travel issues that arise in this wormohole universe are pretty much the same as those that arise in the cylinder universe. However the wormhole calls up considerably more complicated physics. The cylinder universe is just a Minkowski spacetime of ordinary special relativity wrapped up in its entirety at some instant back onto itself. Thus the physics on the cylinder universe is everywhere locally just that of ordinary special relativity. In the wormhole universes, however, we have the complication of making sense of something that looks like a tear in spacetime where each wormhole connects with the main spacetime. Making these wormholes conform with general relativity can require exotic physics.
There is something that looks just a little fishy about the way time travel is arrived at by these cut and past methods. They do not arise from the physics of the spacetime. They come from stipulations on our part that lead to the future wrapping back onto past. Einstein's theory seems only to get involved in so far as it raises no objection. There is nothing wrong with this way of introducing time travel, of course.
It is nice to know, however, that time travel also can arise more naturally without any "cut and paste." The Goedel universe is one such example. This solution to the Einstein equations was arrived at by the famous logician, Kurt Goedel, in the 1940s, when he was a colleague of Einstein's at the Institute for Advanced Study in Princeton, and published in 1949.

The Goedel universe is a solution of Einstein's equations with the cosmological term. Its signature property is that it contains closed timelike worldlines. As a result, it is hard to pick out a single timelike direction globally in the spacetime. Rather, we can get a feel for its spacetime properties by taking just a single two dimensional slice of it. It will become clear that this is not a spacelike slice.
If we consider some observer in the middle of this slice, the observer will find all the matter in a great cosmic rotation around them. (For this reason, the Goedel universe cannot be ours. We don't see such rotation.) The reason for the rotation lies with the structure of spacetime itself. As we consider positions in the slice further away from the observer, the light cones start to tip over. So if we consider a large enough chunk of the slice, we can find a timelike curve that loops back onto itself. It forms a closed timelike curve, the hallmark of universes that admit time travel.
The timelike curve is not a geodesic; it represents the trajectory of an accelerating spaceship. To achieve time travel, the spaceship would need to accelerate quite considerably. Most interestingly, the Goedel universe uses no stipulations about past wrapping back onto the future to achieve the possibility of time travel.
There are other universes that admit time travel. Often rotation is involved. Spacetime around an infinitely long, very dense, rapidly rotating tube of matter admits closed timelike curves, for example. Some of the most fascinating of the time travel universes are those in which one part of spacetime is connected to another by a wormhole. That is just a tunnel of spacetime that provides an alternative route from one part of spacetime to another.
What did Einstein think of time travel universes? He almost never wrote on them. We might never have found out anything of what he thought, except for a fortunate coincidence. Goedel was Einstein's colleague and friend in Princeton at the Institute for Advanced Studies. Goedel wrote a paper describing his Goedel universe for a volume of papers honoring Einstein, Albert Einstein--Philosopher Scientist. Einstein wrote a "Reply to Criticisms" at the end of the volume. It includes his reaction to Goedel's proposal.
 |
Einstein's overall reaction was one of discomfort
but not outright dismissal. He pointed out that the notion of before
and after is messed up in Goedel's universe. That is, if we
have events A and B such that B comes temporally before A we normally think of that as precluding the reverse possibility A comes temporally before B. |
Both can be true in a Goedel universe. Why should we think that only one can hold? Einstein gives only one reason. If B comes before A temporally, then it is possible to send a signal from B to A. Any real signaling process is subject to the the laws of thermodynamics. Therefore it must be unidirectional in time. Its thermodynamic entropy always increases as the signal propagates. A reversed propagation would require that the signal's entropy decreases, in violation of the second law of thermodynamics.
That is all Einstein says. His reference to thermodynamics does call to mind a larger objection that he may have intended us to infer. In a time travel universe, processes travel "all the way round spacetime" and come back to their original states. That contradicts the second law of thermodynamics. Entropy increases along all real processes. That means that the returning states cannot have the same entropy as the initial states to which they must match.
| Here is a picture to give some sense of what this means. At its simplest, the second law of thermodynaics tells us that all systems evolve to states of higher entropy. If, for example, we have lots of energy tied up in our fuels. When we use the fuels to drive our cars, all the energy eventually gets turned into heat. Part of that happens in the burning of the fuel. Part of it happens when we apply the brakes to a fast moving car. The car's energy of motion turns to heat. In a universe without time travel, we might represent this as a gradual warming of the universe. The universe shown at right is colder in earlier times and warmer in later times. This universe is not an expanding universe such as we will see shortly in cosmology. Those universes are expanding and always cooling. |
| If we now try to implement this universal entropic increase in a time travel universe, we will run into trouble. The figure shows a time travel universe that is in a relatively cooler state in the year 2000. As time passes, the entropies of its systems increases and the systems overall grow warmer. These processes evolve all the way back to the present in a much warmer state than they started. The warmed, evolved state arriving in the year 2000 will not match the cooler states that we started with in the year 2000. The mismatch is a failure of the physics that rules out this as a physically possible world. |
| What are we to make of this? Einstein's remark highlights something we already know. A consistent physics in a time travel universe will be unlike our familiar one. A grandfather assassin must fail, even though locally there is no obstacle. Thermal processes must eventually reverse and restore to their original low entropy states, even though the second law of thermodynamics forbids it. Perhaps, at its most liberal, we can read Einstein's hesitation as an affirmation that there is no problem logically in time travel universes, but that their physics would be so different from the one we know that someone interested in understanding our world will pass over them. |
The idea that systems can reduce their entropy is
possible in a statistical physics in which thermodynamic
behavior is recovered as the bulk behavior of very many molecules in
random motion. A gas expands to fill a container because the molecules of the gas scatter as a result of their random motions. The molecules of this gas might just, in an extremely
unlikely coincidence, all collect on one side of a chamber in exactly the same configuration as they had in the past, thereby
spontaneously compressing themselves back to their initial state. Einstein concluded his remarks by wondering whether Goedel's universe might be "excluded on physical grounds." I presume Einstein was alluding to these thermodynamic problems; and to the non-zero value of the cosmological constant Λ, which he then believed should have a value of zero; and perhaps he was alluding to both. |
Here is the full text of Einstein's remarks:
"Kurt Gödel's essay constitutes, in my opinion, an important contribution to the general theory of relativity, especially to the analysis of the concept of time. The problem here involved disturbed me already at the time of the building up of the general theory of relativity, without my having succeeded in clarifying it. Entirely aside from the relation of the theory of relativity to idealistic philosophy or to any philosophical formulation of questions, the problem presents itself as follows:
|
If P is a world-point, a "light-cone" (ds2= 0) belongs to it. We draw a "time-like" world-line through P and on this line observe the close world-points B and A, separated by P. Does it make any sense to provide the world-line with an arrow, and to assert that B is before P, A after P? Is what remains of temporal connection between world-points in the theory of relativity an asymmetrical relation, or would one be just as much justified, from the physical point of view, to indicate the arrow in the opposite direction and to assert that A is before P, B after P? |
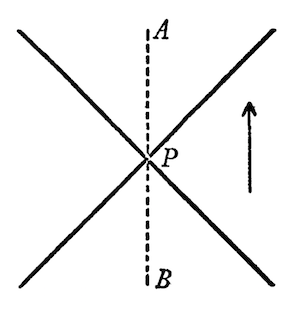 |
In the first instance the alternative is decided in the negative, if we
are justified in saying: If it is possible to send (to telegraph) a signal
(also passing by in the close proximity of P) from B
to A, but not from A to B, then the
one-sided (asymmetrical) character of time is secured, i.e., there exists
no free choice for the direction of the arrow. What is essential in this
is the fact that the sending of a signal is, in the sense of
thermodynamics, an irreversible process, a process which is connected with
the growth of entropy (whereas, according to our present knowledge,
all elementary processes are reversible).
If, therefore, B and A are two, sufficiently
neighbouring, world-points, which can be connected by a time-like line,
then the assertion: "B is before A," makes physical
sense. But does this assertion still make sense, if the points, which are
connectable by the time-like line, are arbitrarily far separated from each
other? Certainly not, if there exist point-series connectable by time-like
lines in such a way that each point precedes temporally the preceding one,
and if the series is closed in itself. In that case the
distinction "earlier-later" is abandoned for world-points which lie far
apart in a cosmological sense, and those paradoxes, regarding the direction
of the causal connection, arise, of which Mr. Gödel has spoken.
Such cosmological solutions of the gravitation-equations (with not
vanishing Λ-constant) have been found by Mr. Gödel. It will be interesting
to weigh whether these are not to be excluded on physical grounds."
"Reply to Criticisms" in Albert
Einstein-Philosopher Scientist. P. A. Schilpp, ed. Open Court,
1951. pp. 687-88.
The spacetime diagram above is taken from Einstein's text. Einstein did not generally use spacetime diagrams in his writing. This is one of the few cases in which he did.
Copyright John D. Norton. March 2001; January 2007; February 16, October 15, 27, 2008. March 6, 2013, March 4, 2015. March 15, 2017. September 1, 5, 2018. Link to "Time Travel with Schoedinger's Cat" added July 23, 2020. February 5, 2022. February 10, 2024. October 22, 2024.