Impossible trident
https://commons.wikimedia.org/wiki/File:Poiuyt--opaque.svg
| HPS 0628 | Paradox | |
Back to doc list
A Budget of Paradoxes
John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
http://www.pitt.edu/~jdnorton
To get us started, here are a few paradoxes. They have been chosen so that they can be stated very briefly. To get a sense of what is to come, it would be helpful to consider how seriously each should be taken and, if they present a serious concern, how they could be answered.
We will start with easier paradoxes and they will get more challenging.
Something is not right with the figures below. Exactly what has gone wrong?
Impossible trident
https://commons.wikimedia.org/wiki/File:Poiuyt--opaque.svg

Penrose stairs
https://commons.wikimedia.org/wiki/File:Penrose_stairs_artwork_SPL.jpg
Reutersvärd’s triangle
https://commons.wikimedia.org/wiki/File:Reutersvärd’s_triangle.svg
What is the sound of one hand clapping?
An irresistible force is one so powerful that
nothing can halt it.
An immovable object is one that nothing can move.
What happens when an
irresistible force meets an immovable object?
Great fleas have little fleas
Upon their backs to bite 'em,
And little fleas have lesser fleas,
and so ad infinitum.
Augustus De
Morgan,
Budget of Paradoxes
(with inspiration from Jonathan Swift)
Which came first? The chicken or the egg?
Each chicken hatches from an egg, so it is not the
first.
Each egg is laid by a chicken, so it is not the first.
The most ancient of fictional cosmologies is the turtle cosmology. The world rides on the back of a giant turtle and thus does not fall. What about the turtle? It rides on the back of another turtle. And then... it's "turtles all the way down."
Each turtle is held up by the turtle under it. What holds up the entire infinite tower?
When we look into a mirror, we see the image reflected in the mirror as having left and right switched. An object held in our right hand will be held in the left hand of the reflected image.
This is puzzling. Why does the mirror switch left and right but not up and down?
Why, for example, if I wear a hat do I not see the hat switched from the top of the reflected image to the bottom of the image?
Are we to think that the mirror knows the difference between left-right and up-down? Somehow it knows to switch things in one direction, but not the other?
We can see that cannot be the way it is if we rotate the mirror by 90 degrees. It still switches left and right only, even though what was up-down in the mirror is now its left-right direction.
Proof that 2 = 1
Let x=1
Multiply both sides by x:
x.x = x.1
x2 = x
Subtract 1 from both sides:
x2 - 1 = x - 1
Factorize the left-hand side:
(x+1)(x-1) = (x-1)
Divide both sides by (x-1):
x+1 = 1
Recall that x=1 and substitute for x:
2 = 1
Proof that 0 = 1
Form the infinite sum of 0's:
0 = 0 + 0 + 0 + 0 + ... (to infinity)
Rewrite 0 as (1-1). The sum is
0 = (1-1) + (1-1) + (1-1) + (1-1) + ...
We can regroup the terms in the sum as
0 = 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ...
0 = 1 - [(1 - 1) + (1 - 1) + (1 - 1) + ...]
Each of the terms (1-1) equals 0:
0 = 1 - [0 + 0 + 0 ...]
The term in the square brackets is the original
sum,
which is 0:
0 = 1 - 0
Simplifying
0 = 1
In 1912 and 1913, Einstein kept a notebook in which he recorded private calculations in preparation for his greatest discovery, the general theory of relativity. Here is the inside cover of the notebook:
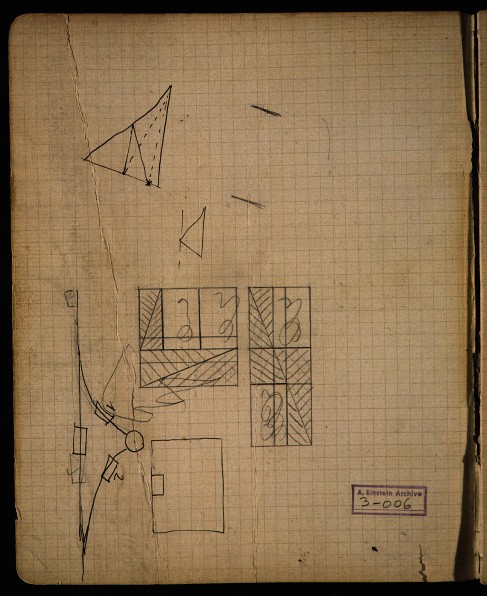
The square and rectangle is a version of a popular recreational puzzle from Einstein's time (and still appears in recreational texts today).
The square occupies an 8x8 section of little squares on the gridded paper. It has an area of 64 little squares.
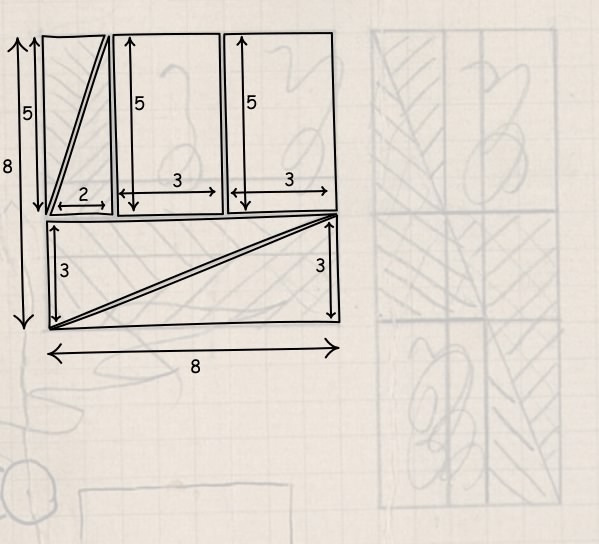
Einstein divides it up into four triangles and two rectangles. They are transferred as indicated to the rectangle on the right. They cover it exactly:
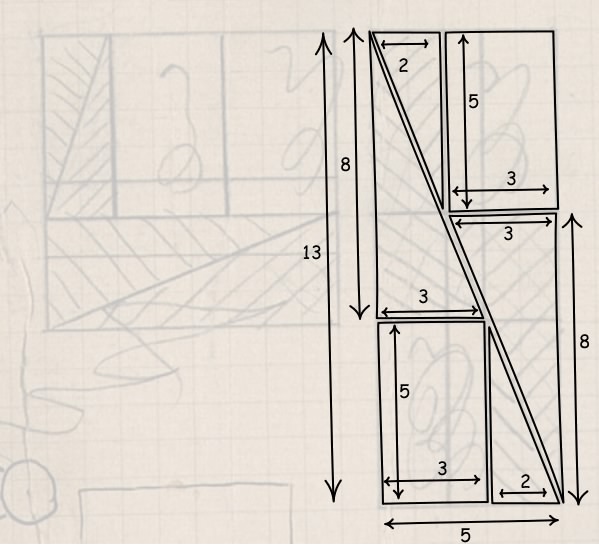
The rectangle occupies a portion of the grid of 5 x 13 little squares. Since it is covered exactly by the parts of the original 8 x 8 square, the two figures have the same area.
But 8 x 8 = 64 and 5 x 13 = 65. So we conclude:
64 = 65
A spaceship leaves earth, traveling at two units of speed. It has a very powerful rocket motor and can repeatedly double its speed. It does so quite rapidly. It doubles its speed at 1/2 minute; and again at 3/4 minute; and again at 7/8 minute; and so on for the full minute.
Here is a schedule of its speeds and distances covered in each of the indicated time intervals
| Time interval | speed | distance covered = speed x time |
| 0 to 1/2 = 1/2 | 2 | 1 |
| 1/2 to 3/4 = 1/4 | 4 | 1 |
| 3/4 to 7/8 = 1/8 | 8 | 1 |
| 7/8 to 15/16 = 1/16 | 16 | 1 |
| etc, | etc | etc |
There are infinitely many of these time intervals in which the spaceship's speed doubles. In each of them, the spaceship covers the same unit distance. That is, at the end of one minute, the spaceship has traveled a distance:
1 + 1 + 1 + 1 + 1 + 1 + ... = ∞
The simple reading of this result is just that the spaceship is "at infinity" after a minute.
That makes no sense. Every position in space is some finite distance from us. The distance might be very large: a light year, a million light years, a hundred billion light years, and so on. But they are always at some finite distance from us, even if it is very large. There is no place "infinity."
Where is the spaceship after one minute?
Modern cosmology depicts the universe as filled with matter in galaxies. There are two foundational properties:
• The matter of the universe, at the level of galaxies, is expanding.
• Everywhere in the universe is the same on the largest scale. Matter is expanding everywhere.
This is how the expansion looks as cosmic time passes. Pick some region of space and, on the large scale, matter leaves it. The total matter in the region decreases.
This is how the universe looks everywhere.
The puzzle: if matter in every region is decreasing with the expansion, where is all the matter going?
A lamp is switched on at one minute to midnight; off at 1/2 minute to midnight; on at 1/3 minute to midnight; off at 1/4 minute to midnight; and so on all the way to midnight. By midnight, an infinity of switchings has been completed.
single lamp from https://commons.wikimedia.org/wiki/File:Idea_lightbulb_silhouette.svg
Here's the sequence in a table.
| Time before midnight | lamp |
| 1 | ON |
| 1/2 | OFF |
| 1/3 | ON |
| 1/4 | OFF |
| etc. | etc |
The puzzle: At midnight, is the lamp ON or OFF?
It cannot be ON, since each moment at which the lamp is switched on is followed by another moment at which it is switched off.
It cannot be OFF, since each moment at which the lamp is switched off is followed by another moment at which it is switched on.
At a carnival sideshow, you are invited to play the following game. There are three cards. One is blue on both sides. One is red on both sides. One is blue on one side and red on the other.
To play the game, you are allowed to shuffle and flip the cards without looking until they could be in any order with any side up.
A card is drawn and it is red. You are offered an even odds bet that the other side of the card is blue.
It seems a fair bet since there are only two choices: red or blue; and you mixed the cards thoroughly.
Is it a fair bet?
It is not. Why not?
A camper wandered away from the campsite in the middle of a desert and is lost. The search party sets out to find the camper. They draw two circles on their map. One is one mile in radius. The other is two miles in radius.
The searchers expect the lost camper to be somewhere within the two circles. Otherwise they are completely uncertain over the lost camper's position.
One searcher reasons: our lost camper is as likely to be one mile away as two miles away. So the lost camper is equally likely to be in the outer ring as in the inner circle.
Another searcher reasons: the outer ring is three times the area of the inner circle. So the lost camper is three times more likely to be in the outer ring as in the inner circle.
They cannot both be right. Who is right?
An ordinary lottery chooses without favor among a large but finite number of balls numbered 1, 2, ..., N. An infinite lottery machine chooses without favor, but from all infinity of balls numbered 1, 2, 3, ... and so on to infinity.
Two infinite lottery machines will choose a number. The first, blue machine produces blue colored balls. The other, red machine produces red colored balls.
Will the red machine select a number greater than
the blue machine? It seems so. For when the blue machine is run, it must
select some ball. Imagine, for example, that the number is 3. Then the red
machine will select a number less than or equal to 3 only in finitely many
cases. It could choose 1 or 2 or 3. However there are infinitely
many ways the red machine can choose a number greater than 3. It
could choose 4, 5, 6, 7, 8, 9, 10, 11, ...
Since each ball has an equal chance of being selected, the chances are infinitely greater than the red machine will choose a number greater than 3.
This favoring of the red machine is true no matter which number the blue machine selects. If the blue machine selects 1,000,000,000, there are still infinitely more numbers the red machine can choose that are greater, but only finitely many that are fewer.
The operator of the blue machine is sure that the red machine will select a greater number.
The puzzle: The operator of the red machine carries out exactly the same inferences and concludes that the blue machine is sure to select a greater number.
Both cannot be correct.
There are many paradoxes associated with the assumption that our world has an infinite past in time.
Here is a version of one, attributed by A. W. Moore, The Infinite, 3rd ed. p 47 to Philoponous:
In any time period, there are always twelve times as many months as there are years.
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| Year | |||||||||||
If, however, the universe has existed infinitely into the past, then as many months as years will have elapsed. They are both infinite in number.

Immanuel Kant gave a celebrated argument against an infinite past through his antinomies of pure reason in his Critique of Pure Reason:
"THESIS.
The world has a beginning in time...
Granted that the world has no beginning in time;
up to every given moment of time, an eternity must
have elapsed, and therewith passed away an infinite series of
successive conditions or states of things in the world. Now the infinity
of a series consists in the fact that it never can be completed by means
of a successive synthesis. It follows that an infinite series already
elapsed is impossible and that, consequently, a beginning of the world
is a necessary condition of its existence. And this was the first thing
to be proved."
To get a sense of his argument, imagine that the world began some 100,000,000 years ago. We can count off the years elapsed since then:
1, 2, 3, ..., 100, ..., 1,000, ..., ...,
100,000
This "counting off" is a process of successive synthesis. With a beginning in time some finitely many years ago, it can be completed. If there is no beginning in time, the process fails. It can never start.
Another approach is to imagine counting backwards into the past, starting at now, given the number 0:
0 -1, -2, -3, ..., -100, ..., -1,000, ...
If there is no beginning to the world, the process can never be completed. No matter how far into the past we count, there are always more numbers to count.
What complicates matters is that Kant also gave an argument that the world cannot have a beginning in time either.
"ANTITHESIS.
The world has no beginning...
PROOF.
For let it be granted that it has a beginning. A beginning is an
existence which is preceded by a time in which the thing does not exist.
On the above supposition, it follows that there must have been a time in
which the world did not exist, that is, a void time. But in
a void time the origination of a thing is impossible; because
no part of any such time contains a distinctive condition of being, in
preference to that of non-being (whether the supposed thing originate of
itself, or by means of some other cause). Consequently, many series of
things may have a beginning in the world, but the world itself cannot
have a beginning, and is, therefore, in relation to past time,
infinite."
Kant imagines that the world began say, here, in time:
The trouble is that there are times, Kant supposes, prior to this beginning devoid of any worldly presence. But these times are all exactly alike. They are pure, empty times. A void. Nature would have no reason to choose this time rather than some earlier time, such as this:
Or an even earlier time such as this:
If Nature cannot choose a time for the beginning, the beginning cannot happen.
It would seem that something has gone astray here. Modern cosmologies consider both cases of universes with finite pasts and universes with infinite pasts without any sense of paradox. What has gone wrong?
To think about for the next class:
Which paradoxes are interesting? Why are they so?
Which paradoxes are less troubling? Why are they so?
Which paradoxes are worrisome? What can you do about it?
May 29, 2021;
December 18, 2022.
Copyright, John D. Norton