Paradoxes of Measure

John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
http://www.pitt.edu/~jdnorton

There are two paradoxes initiated in antiquity whose full treatment requires ideas about the sizes of sets and the notion of measure that were not fully developed until the 19th and 20th centuries. Both paradoxes are easy to state, but present real obstacles to attempts at a resolution until these new ideas became available. They are Zeno's paradox of measure and the paradox of Aristotle's wheel.

Aristotle on Zeno's Paradox of Measure

Translation from The Complete Works of Aristotle, ed. J. Barnes, Princeton University Press, 1984. On Generation and Corruption. pp. 6-7. starting 316a15 A detailed account of the paradox and its modern resolution is provided by Brian Skyrms, "Zeno's Paradox of Measure" in R. S. Cohen and L. Laudan (eds.), Physics, Philosophy and Psychoanalysis, Dordrecht: Reidel, 1983, pp. 223-254.

The standard account of Zeno's paradox of measure in the ancient Greek tradition is provided by Aristotle in his work, On Generation and Corruption. He considers whether bodies can be infinitely divisible. That is, if we take a body such as a stick, is it possible in principle for it to be divided at any position on the stick. Admission of this possibility leads to a dilemma:

   "For to suppose that a body (i.e. a magnitude) is divisible through and through, and that this division is possible, involves a difﬁculty. What will there be in the body which escapes the division?
     If it is divisible through and through, and if this division is possible, then it might be, at one and the same moment, divided through and through, even though the dividings had not been effected simultaneously; and the actual occurrence of this result would involve no impossibility. Hence whenever a body is by nature divisible through and through, whether by bisection, or generally by any method whatever nothing impossible will have resulted if it has actually been divided for if it has been divided into innumerable parts, themselves divided innumerable times, nothing impossible will have resulted, though perhaps nobody in fact could so divide it.
     Since, therefore, the body is divisible through and through, let it have been divided. What, then, will remain? A magnitude? No: that is impossible, since then there will be something not divided, whereas ex hypothesi the body was divisible through and through. But if it be admitted that neither a body nor a magnitude will remain, and yet division is to take place, the body will either consist of points (and its constituents will be without magnitude) or it will be absolutely nothing. If the latter, then it might both come-to-be out of nothing and exist as a composite of nothing; and thus presumably the whole body will be nothing but an appearance. But if it consists of points, it will not possess any magnitude. For when the points were in contact and coincided to form a single magnitude, they did not make the whole any bigger (since, when the body was divided into two or more parts, the whole was not a bit smaller or bigger than it was before the division); hence, even if all the points be put together, they will not make any magnitude."

See Simplicius, On Aristotle's Physics. Trans. P. Huby and C. C. W Taylor. Bristol Classics Press, 2011, p. 51. The attribution is accepted in Nick Huggett, "Zeno’s Paradoxes", The Stanford Encyclopedia of Philosophy, Edward N. Zalta (ed.), https://plato.stanford.edu/archives/win2019/entries/paradox-zeno/ Section 2.3.

What is immediately problematic here is that Aristotle does not attribute the argument to Zeno. It has been traditional, however, to attribute the argument to Zeno perhaps on the strength of remarks by a much later commentator on Aristotle, Simplicius. I will follow this tradition and describe the paradox as one of Zeno's.

The argument Aristotle presents has the form of a reductio of the assumption that matter is infinitely divisible. That is, it is assumed that we can divide a body at any point. This entails that it has no smallest part of non-zero magnitude. For were there to be any part of non-zero magnitude, we could by assumption divide it further into smaller parts.

At first it seems that Aristotle is imagining some sort of supertask in which we take some body, divide it; and divide it again; and so on infinitely until it is broken up into its infinite parts. While it might be helpful to imagine a supertask effecting the division, a supertask is not needed to make good on the argument. Aristotle needs only to imagine that matter consists of parts that join and that the joins everywhere dissolve. We are left with the smallest parts, exposed and detached from each other.

To get a sense of the point, consider a brick wall. Its parts, the bricks, are held together by mortar.

Now imagine that the mortar just dissolves away. We would be left with the disconnected parts, the bare bricks, without any connecting mortar.

When Aristotle writes of the body divided "through and through," we are to imagine the same thing for an infinitely divisible body. Its smallest parts would just be laid bare.

Both cases lead to a contradiction with the assumption that the full body has non-zero magnitude. Taking each case in turn:

If the smallest part is a point of zero magnitude, then we cannot reconstitute the points into a body of non-zero magnitude. For any compositions of zero magnitude remains zero in magnitude. We might imagine this inference to look like this:

If the smallest parts are nothings, then the situation is worse. Composing nothings can only give more nothing:

The reductio is complete. Each horn of the dilemma leads to a contradiction with the assumption that there are infinitely divisible, extended bodies.

This paradox proved to be one that ancient thinkers found hard to deal with. Aristotle reported that this paradox provided a strong basis for Democritus to defend his notion of atoms:

Aristotle, On Generation and Corrruption, 316a14, 317a1

"Democritus would appear to have been convinced by arguments appropriate to the subject, i.e. drawn from the science of nature..."

"Such is the argument which is believed to establish the necessity of atomic magnitudes..."

Democritus argued that all matter consists of atoms, that is, small, indivisible extended magnitudes "a-tom" = "without parts." If that is so, then the division "through and through" required by Aristotle's narrative cannot be completed and the paradox is avoided.

Aristotle's resolution was equally severe. In one response, he retracted to the idea of a potential infinity. A body, he allowed, can be divided finitely many times. However the complete division of the paradox requires an actual infinity of divisions. Such an actuality is opposed by Aristotle. (See Skyrms, p. 230 for a second response by Aristotle.)

Aristotle's Wheel (Rota Aristotelica)

The paradox known as Aristotle's wheel is traditionally attributed to Aristotle, as the name suggests. However it appears in a collection of mechanical problems written later and only by tradition connected with Aristotle. The connection is close enough for the collection of problems in mechanics to be included in an edition of the Complete Works of Aristotle as Mechanics. The editorial introduction however notes that "the spuriousness [of the attribution to Aristotle] has never been doubted."

Translation from The Complete Works of Aristotle, ed. J. Barnes, Princeton University Press, 1984. Mechanics, p. 17.

Problem 24 in the collection begins with a synoptic statement of problem. It reads:

"§ 24 · There is a question why a large circle traces out a path equal to that of a smaller circle, when they are placed about the same centre, but when they are rolled separately, their paths are to one another in the proportion of their dimensions. And, further, the centre of both being one and the same, at one time the path which they trace is of the same length as the smaller traces out alone, and at another time of the length which the larger circle traces. Now it is manifest that the larger circle traces out the longer path. For by mere observation it is plain that the angle which the circumference of each makes with its own diameter is greater in the case of the larger circle than in the smaller; so that, by observation, the paths along which they roll will have this same proportion to one another. But, in fact, it is manifest that, when they are situated about the same centre, this is not so, but they trace out an equal path; so that it comes to this, that in the one case the path is equal to that traced by the larger circle, in the other to that traced by the smaller."

What then follows is a detailed geometrical construction giving more precise details of the problem just sketched. Here I will give a simplified presentation of the argument. The full text of the geometrical constructions is reproduced here.

The paradox considers two circles of unequal sizes. Let us consider one to be double the size of the other. That means that the circumference of the larger circle is twice that of the smaller one, since we have the relation in Euclidean geometry:

If these circles are wheels, we can roll each along a flat surface for one complete rotation. The distances along which they roll equal their circumferences. The larger wheel will unroll a distance BB' twice that of the smaller wheel AA'.

Matters are otherwise, however, if we connect the two circles together into the same figure. Then when we unroll the wheel with the two circles, we find that each unrolls the same distance. That is, the unrolled circumferences AA' and BB' are equal.

Since the distances are the circumferences of the circles, we have found that the two circles have the same circumference, even though they are of different sizes, in contradiction with the well known geometry of circles.

To reinforce this conclusion, the narrative traces the alignments of points as the combined circles unroll. Consider some radius of the concentric circles OCD. When the wheel has rolled sufficiently that OC is perpendicular to the surface on which the wheel rolls, then OD will also be perpendicular to the surface. It follows that the lengths of the two circumferences unrolled, AC and BD are equal.

This is true for any radius we may have considered. At any moment in the process, the lengths of circumferences unrolled are the same.

The problem conceived dynamically

An older survey is Israel E. Drabkin, "Aristotle's Wheel: Notes on the History of a Paradox," Osiris, 9 (1950), pp. 162-198.

Aristotle's wheel enjoyed a long and vexed history as later thinkers grappled with the difficulties it raised. What is interesting, however, is that, as far as I can see, the original problem was straightforward and straightforwardly solved in the subsequent discussion in the Mechanics itself.

The original problem was conceived as a problem in the mechanics of real physical bodies and the physical forces that lead to motions. What really happens, it asks, were we to roll a wheel consisting of two concentric circles, one smaller than the other.

We can make the dynamically conceived version of the problem more vivid by recalling an example that does not come from Aristotle's time. This version is implemented in the rolling of a railway train wheel on a rail. These wheels have the two circles of Aristotle's conception. There is the rim of the wheel that will sit on the rails; and there is a flange that extends beyond the rim.

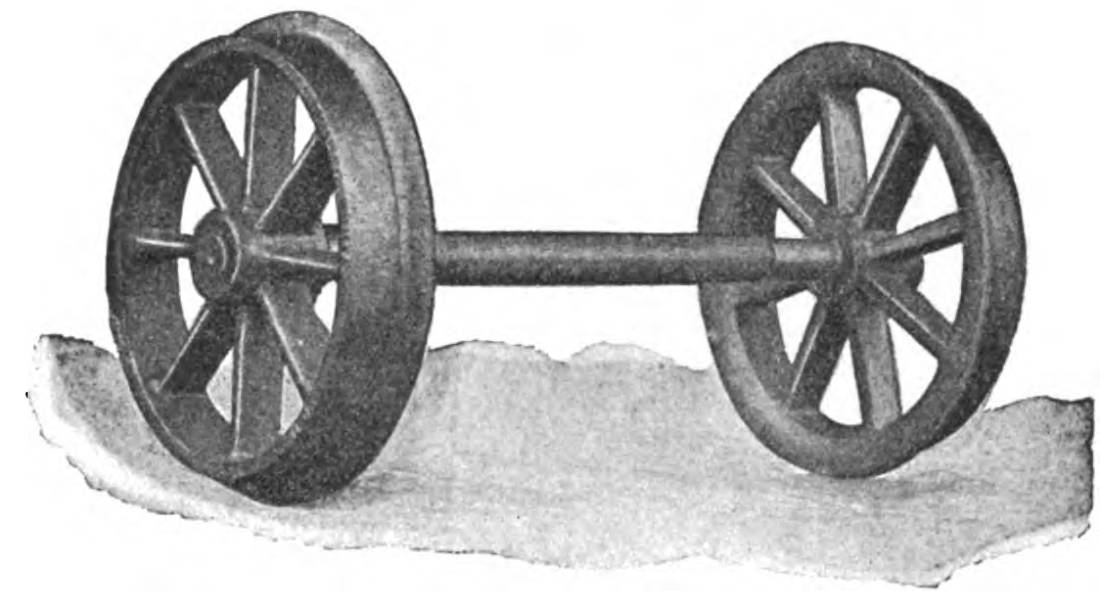
In use, the rim sits on the rail and the wheel turns as the supported vehicle moves along the rails.

Figure from Manning, Maxwell and Moore, Illustrated Catalogue of Railway, Steamship, Machinist, Factory, Mill and Electric Supplies. Pittsburgh, 1902.

Returning to the ancient exposition, we are told that the problem is not fully defined until we determine which of the two circles is driving the other. There are two cases, according to whether the smaller is driving the larger circle; or the larger circle is driving the smaller.

We might imagine this first case to be when the smaller circle rolls without slipping on a rail and thereby holds back the larger circle. To see what happens, consider a radius that intersects the smaller and the larger circle at two points, shown in the figure. If the circle rolls forward, at the moment at which the radius points vertically downwards, the point on the smaller circle will be in contact with the rail and will be momentarily at rest. The point on the larger circle, however, at this moment, will be moving backwards.

If we imagine the larger circle also to be in contact with its own rail, its motion will be a combination of rolling and skidding backwards of the point of contact with the rail. With the backward motion of the edge of the outer circle, both circles are transported through a distance equal to the circumference of the smaller circle.

The various points on the wheel trace out curves in space known as "cycloids." They were investigated by Galileo in the 17th century and had a major place in geometry afterwards.

The trajectory traced by a point on the rim of the wheel, in contact with the rail, is a simple cycloid, part of which is shown here:

A point on the edge of the flange that extends beyond the rail traces out a prolate cycloid, part of which is shown here:

The loop at the bottom corresponds to the portion of the motion in the reverse direction. Finally, for completeness, a point in the interior of the wheel, above the rail, traces a curate cycloid, part of which in shown here:

The second case is the reverse of the first. We now imagine the larger circle to roll without slipping. It drags the smaller circle forward. The motion of the smaller circle will be a combination of rolling and skidding forward of the point of contact with its rail. Then both are transported through a distance equal to the circumference of the larger circle.

This second case is roughly akin to the motion of an automobile tire. The outer rim of the tire rolls along the road. The inner rim, however, makes no contact with the road. If it did contact some raised rail laid out along the road, however, then its motion would be the rolling and skidding described.

Images: Victor W. Pagé, The Modern Gasoline Automobile. New York: Norman W. Henley Publishing Co., 1912, pp. 68, 514.

To see more vividly how the second case unfolds, we might imagine that both wheels carry elastic treads around their circumferences and that these treads unroll as the wheels turn. The figure below represents the case of the larger wheel rolling without slipping. It follows that the smaller wheel is dragged through a greater distance. The elastic tread unrolling from the circumference of the smaller circle is stretched, as shown in the figure.

This quite complete analysis seems to me to be plainly how the problem is treated and solved in the Mechanics. After the text above that sets up the problem, the Mechanics then provides its solution. Here is a part of the solution that gives its main ideas:

     "Let there be two circles, a greater A and a lesser B. If the lesser were to push along the greater, when the greater is not rolling alone, it is plain that the greater will traverse so much distance as it has been pushed by the lesser. And it has been pushed the same distance as the small circle has moved; so that they have both traversed an equal straight line.
     Necessarily, therefore, if the lesser be rolling while it pushes the greater, the latter will be rolled, as well as pushed, just so far as the lesser has been rolled, if the greater have no motion of its own; for in the same way and so far as the moving body moves it, so far must the body which is moved be moved thereby. So, indeed, the lesser circle has moved the greater so far and in the same way, viz., in a circle and for the distance of one foot (for let that be the extent of the movement); and consequently the larger circle has moved that distance.
     So too, if the large circle move the lesser, the lesser circle will have been moved just as far as the large circle, in whatever way the latter be moved, whether quickly or slowly, by its own motion; and the lesser circle will trace out a line at the same velocity and of the same length as the greater traced out by its natural movement...""

The problem conceived geometrically

As time passed, this straightforward problem in the dynamics of rolling bodies migrated into a deeper and richer problem that greatly taxed the resources of analysts up to the 19th century. The problem is one of geometry and can be separated from issues of rolling bodies and forces that lead to them roll. It resides in a contradiction between two propositions in geometry.

The first proposition is the familiar result stated above for circles in Euclidean geometry:

Consider a larger circle of twice the diameter or twice the radius of a smaller circle. It follows that the circumference of the larger circle is twice that of the smaller circle. In increasing the size of the smaller circle, the two lengths--radius and circumference--maintain their proportions. If the radius doubles, then so does the circumference.

The second proposition is one suggested by the original wheel construction. The circumference of each circle consists of an infinity of points. We can put the points of the circles in a one-to-one correspondence with the points of the larger circle. The correspondence is implemented by radii of the circle, or, if one wants to think a little physically, the infinite spokes of a physical wheel.

If the two circles have exactly as many points as each other, then they have the same properties, including in particular their lengths.

That is, we have found two arguments that lead to a contradiction. The circumference of the larger circle is greater than that of the smaller circle; and the circumference of the larger circle is equal to that of the smaller circle.

What I find striking is that this geometrical argument can be made without any discussions of physical wheels and what happens when they roll. The figure of the circle above with the radii implementing the one-to-one correspondence suffices. For this reason, on my reading, the original version of the problem in Aristotle's Mechanics was not concerned with this geometrical problem. Perhaps there was some sense of it lurking in the background, but that distant sense seems me to be the best we can say of its possible presence.

Galileo Galilei

These two versions of the problem of Aristotle's wheel do not exhaust the place that the problem has in the history of geometry and science. Perhaps the most intriguing analysis is in Galileo's Two New Sciences of 1638 It is a founding document of the seventeenth century scientific revolution. The work consists of four days of dialog. The first two develop the science of statics and the strength of materials. The third and fourth day are best know since they develop the science of motion. They present Galileo's law of fall: that all bodies fall alike such that the total distances fallen increase as squares with the time of fall.

In Day one, in the midst of this analysis, Galileo introduces Aristotle's wheel. His goal is to develop an account of the fundamental structure of matter.

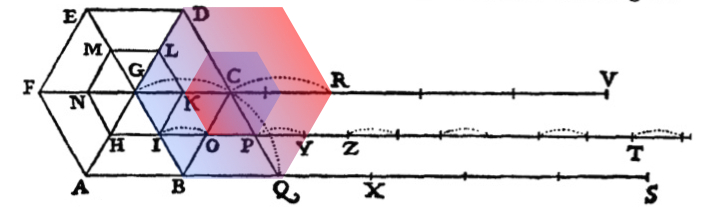
To proceed, Galileo first treats polygons instead of circles. His figure, reproduced below, depicts the case of a hexagon.

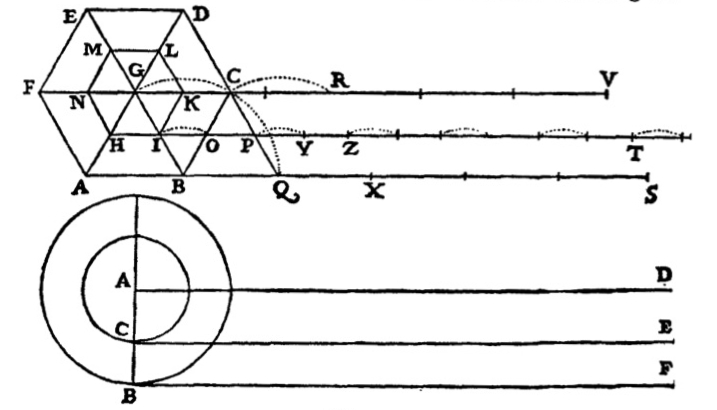
The behavior of a circle is then recovered by considering what happens as the number sides of the polygon become infinitely great. A circle, for Galileo, is an infinite-sided polygon. Galileo takes the case of the outer circle rotating without slipping. It follows, as we have seen, that the smaller circle moves with a combination of a rotating motion and a jumping such that the overall displacement of the smaller circle is increased to match the displacement of the larger circle.

This combination of motions is illustrated in Galileo's figure above. It takes the case of the hexagonal approximation to the circle and has the larger hexagon rotating without slippage. The dotted lines then indicate the resulting motion. When the center G moves to C, as indicated by the dotted lines connecting them, the side IK of the smaller hexagon jumps to position OP. The dotted line connection I to O indicated the jump. Adding shaded hexagons to Galileo's figure shows the jump a little more clearly.

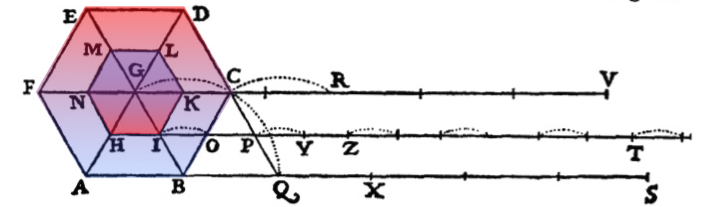
The larger hexagon rolls through 60 degrees, pivoting about point B, so that BC ends up at BQ.

The motion of the inner hexagon is a combination of a rotation through 60 degrees and a jump of the side IK to position OP.

By "mathematically incoherent," I mean that if we try to construct such a system by taking an infinite limit, we find that the limiting procedure produces inconsistent results. That judgment, of course, requires techniques of later developments, so it is not a criticism of Galileo.

Galileo uses the jumping in the polygonal construction as a basis for inferring that the same sort of jumping happens when a pair of circles roll in the same way. Since the limit of the polygons is a circle with, loosely speaking, infinitely many infinitely small sides, reliably visualizing how this can be transcends ordinary imagination. This did not deter Galileo. He concluded that the circumferences of the circles consist of infinitely many points with infinitely many small empty spaces between them. Why Galileo might find this proposal appealing is at first hard to see. It is both wildly imaginative and mathematically incoherent. We have some clues in the subsequent discussion. He writes:

Galileo Galilei, Dialogues Concerning Two New Sciences. Trans Henry Crew and Alfonso di Salvio. New York: MacMillan, 1914. pp. 25-26. Text online at https://oll.libertyfund.org/title/galilei-dialogues-concerning-two-new-sciences#preview

"And here I wish you to observe that after dividing and resolving a line into a finite number of parts, that is, into a number which can be counted, it is not possible to arrange them again into a greater length than that which they occupied when they formed a continuum [continuate] and were connected without the interposition of as many empty spaces. But if we consider the line resolved into an infinite number of infinitely small and indivisible parts, we shall be able to conceive the line extended indefinitely by the interposition, not of a finite, but of an infinite number of infinitely small indivisible empty spaces."

This text appears to offer a solution to the geometrical version of the problem of Aristotle's wheel. In it, we must address the difficulty that the number of points in the smaller and larger circles are the same.

Galileo does not consider the case of parts that become arbitrarily small, in which case an infinity of them may be needed.

Galileo first considers the possibility that the circle's constitutive parts are extended magnitudes, that is, parts of non-zero length. Then only finitely many are needed to form a circle. In that case, Galileo correctly notes, we run into trouble if we can map the parts of the smaller circumference to the larger circumference, always matching a like part with a like part. If their extended parts match in this way, the two circumferences must have the same length. For there is no way to reorganize these finitely many, extended parts of the circumference of the smaller circle to recover a circle of larger circumference. Euclidean geometry is contradicted.

Galileo then turns to the next case. Each circumference consists of infinitely many points of zero magnitude, that is, points that cannot be divided into smaller parts. Then, presumably, the points by themselves cannot be responsible for the extension of the circumferences. That extension must come from infinitely many, infinitely small empty spaces between the points. Now it is possible to map the points of the smaller and larger circumferences one-to-one without requiring that their lengths be the same. For their lengths come from the empty spaces between the points. The larger circumference has larger spaces and thus larger lengths.

We shall see that this resolution has some affinity with the modern treatment of the geometric version of Aristotle's wheel of the next chapter. There we shall see that we separate the points of a continuum from its length properties, which are treated separately by a measure. Whether this is what Galileo had in mind is not a question that we can answer. Galileo wrote 300 years before Gauss and Riemann introduced these conceptions.

To Ponder

Democritus used Zeno's paradox of measure as an argument for the existence of atoms. How cogent is this argument? Does it force us to conclude that space must consist of non-zero magnitude spatial atoms and that time consists of non-zero magnitude temporal atoms?

Is a line such as the circumference of a circle nothing but a set of points? If so, why are the two circumferences not the same in all their properties, including length? But if they differ, what extra property is there that distinguishes them?


	Much of these first two days was devoted to quite practical problems in statics and the strength of materials. Here Galileo asks what happens to the bending moment of the cantilevered beam about point A when the length of the beam is increased by the piece BE. The answer is that the bending moment increases with the square of the length of the beam.