MATH2071: LAB 5: Norms, Errors and Whatnot

Introduction	Exercise 1
Vector Norms	Exercise 2
Matrix Norms	Exercise 3
Compatible Matrix Norms	Exercise 4
More on the Spectral Radius	Exercise 5
Types of Errors	Exercise 6
A matrix example	Exercise 7
Extra credit: the determinant	Exercise 8
	Exercise 9
	Extra Credit

Introduction

The objects we work with in linear systems are vectors and matrices. In order to make statements about the size of these objects, and the errors we make in solutions, we want to be able to describe the ``sizes'' of vectors and matrices, which we do by using norms.

We then need to consider whether we can bound the size of the product of a matrix and vector, given that we know the ``size'' of the two factors. In order for this to happen, we will need to use matrix and vector norms that are compatible. These kinds of bounds will become very important in error analysis.

We will then consider the notions of forward error and backward error in a linear algebra computation.

We will then look at one useful matrix example: a tridiagonal matrix with well-known eigenvalues and eigenvectors.

This lab will take two sessions.

Vector Norms

A vector norm assigns a size to a vector, in such a way that scalar multiples do what we expect, and the triangle inequality is satisfied. There are four common vector norms in dimensions:

The vector norm

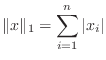
$\displaystyle \Vert x\Vert _{1} = \sum_{i=1}^n \vert x_{i}\vert$
The (or ``Euclidean'') vector norm

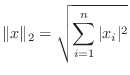
$\displaystyle \Vert x\Vert _{2} = \sqrt{\sum_{i=1}^n \vert x_{i}\vert^{2} }$
The vector norm

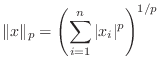
$\displaystyle \Vert x\Vert _{p} = \left(\sum_{i=1}^n \vert x_{i}\vert^{p}\right)^{1/p}$
The $L^\infty$ vector norm

$\displaystyle \Vert x\Vert _{\infty} = \max_{i=1,\ldots,n} \vert x_{i}\vert$

To compute the norm of a vector in Matlab:

$\Vert x\Vert _{1} =$ norm(x,1);
$\Vert x\Vert _{2} =$ norm(x,2)= norm(x);
$\Vert x\Vert _{p} =$ norm(x,p);
$\Vert x\Vert _{\infty} =$ norm(x,inf)

(Recall that inf is the Matlab name corresponding to $\infty$ .)

Exercise 1: For each of the following column vectors:

   x1 = [ 4; 6; 7 ]
   x2 = [ 7; 5; 6 ]
   x3 = [ 1; 5; 4 ]

compute the vector norms, using the appropriate Matlab commands. Be sure your answers are reasonable.

        L1            L2            L Infinity

  x1    __________    __________    __________
  x2    __________    __________    __________
  x3    __________    __________    __________

Matrix Norms

A matrix norm assigns a size to a matrix, again, in such a way that scalar multiples do what we expect, and the triangle inequality is satisfied. However, what's more important is that we want to be able to mix matrix and vector norms in various computations. So we are going to be very interested in whether a matrix norm is compatible with a particular vector norm, that is, when it is safe to say:

$\displaystyle \Vert Ax\Vert \le \Vert A\Vert \Vert x\Vert$

There are four common matrix norms and one ``almost'' norm:

The or ``max column sum'' matrix norm:

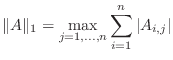
$\displaystyle \Vert A\Vert _{1} = \max_{j=1,\ldots,n} \sum_{i=1}^n \vert A_{i,j}\vert$

Remark: This is not the same as the norm of the vector of dimension whose components are the same as $A_{i,j}$ .
The matrix norm:

$\displaystyle \Vert A\Vert _{2} = \max_{j=1,\ldots,n}\sqrt{\lambda_{i}}$

where $\lambda_{i}$ is a (necessarily real and non-negative) eigenvalue of or

$\displaystyle \Vert A\Vert _{2} = \max_{j=1,\ldots,n}\mu_{i}$

where $\mu_{i}$ is a singular value of ;
The $L^\infty$ or ``max row sum'' matrix norm:

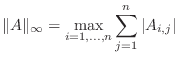
$\displaystyle \Vert A\Vert _{\infty} = \max_{i=1,\ldots,n} \sum_{j=1}^n \vert A_{i,j}\vert$

Remark: This is not the same as the $L^\infty$ norm of the vector of dimension whose components are the same as $A_{i,j}$ .
There is no matrix norm in Matlab.
The ``Frobenius'' matrix norm:

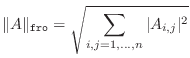
$\displaystyle \Vert A\Vert _{\mathtt{fro}} =\sqrt{\sum_{i,j=1,\ldots,n} \vert A_{i,j}\vert^{2}}$

Remark: This is the same as the norm of the vector of dimension whose components are the same as $A_{i,j}$ .
The spectral radius (not a norm):

$\displaystyle \rho(A) =\max \vert\lambda_{i}\vert$

(only defined for a square matrix), where $\lambda_{i}$ is a (possibly complex) eigenvalue of .

To compute the norm of a matrix in Matlab:

$\Vert A\Vert _{1} =$ norm(A,1);
$\Vert A\Vert _{2} =$ norm(A,2)=norm(A);
$\Vert A\Vert _{\infty} =$ norm(A,inf);
$\Vert A\Vert _{\mathtt{fro}} =$ norm(A,'fro')
See below for computation of $\rho(A)$ (the spectral radius of )

Compatible Matrix Norms

A matrix can be identified with a linear operator, and the norm of a linear operator is usually defined in the following way.

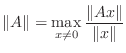
$\displaystyle \Vert A\Vert = \max_{x\ne0} \frac{\Vert Ax\Vert}{\Vert x\Vert}$

(It would be more precise to use $\sup$ rather than $\max$ here but the surface of a sphere in finite-dimensional space is a compact set, so the supremum is attained, and the maximum is correct.) A matrix norm defined in this way is said to be ``vector-bound'' to the given vector norm.

In order for a matrix norm to be consistent with the linear operator norm, you need to be able to say the following:

$\displaystyle \Vert Ax\Vert \leq \Vert A\Vert \Vert x\Vert$

(1)

but this expression is not necessarily true for an arbitrarily chosen pair of matrix and vector norms. When it is true, then the two are ``compatible''.

If a matrix norm is vector-bound to a particular vector norm, then the two norms are guaranteed to be compatible. Thus, for any vector norm, there is always at least one matrix norm that we can use. But that vector-bound matrix norm is not always the only choice. In particular, the matrix norm is difficult (time-consuming) to compute, but there is a simple alternative.

Note that:

The , and $L^\infty$ matrix norms can be shown to be vector-bound to the corresponding vector norms and hence are guaranteed to be compatible with them;
The Frobenius matrix norm is not vector-bound to the vector norm, but is compatible with it; the Frobenius norm is much faster to compute than the matrix norm (see Exercise 5 below).
The spectral radius is not really a norm and is not vector-bound to any vector norm, but it ``almost" is. It is useful because we often want to think about the behavior of a matrix as being determined by its largest eigenvalue, and it often is. But there is no vector norm for which it is always true that

$\displaystyle \Vert Ax\Vert \le \rho(A) \Vert x\Vert.$

There is a theorem, though, that states that, for any matrix , and for any chosen value of $\epsilon>0$ , a norm can be found so that $\Vert Ax\Vert\leq (\rho(A)+\epsilon)\Vert x\Vert$ . Note that the norm depends both on $\epsilon$ and .

Exercise 2: Consider each of the following column vectors:

   x1 = [ 4; 6; 7 ];
   x2 = [ 7; 5; 6 ];
   x3 = [ 1; 5; 4 ];

and each of the following matrices

A1 = [38   37   80
      53   49   49
      23   85   46];

A2 = [77   89   78
       6   34   10
      65   36   26];

Check that the compatibility condition (1) holds for each case in the following table by computing the ratios

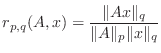
$\displaystyle r_{p,q}(A,x)=\frac{\Vert Ax\Vert _q}{\Vert A\Vert _p\Vert x\Vert _q}$

and filling in the following table. The third column should contain the letter ``S'' if the compatibility condition is satisfied and the letter ``U'' if it is unsatisfied.

Suggestion: I recommend you write a script m-file for this exercise. If you do, please include it with your summary.

Matrix  Vector        
 norm    norm   S/U   r(A1,x1)   r(A1,x2)    r(A1,x3)    r(A2,x1)    r(A2,x2)    r(A2,x3)
  (p)     (q)        

   1      1     ___   _________  __________  __________  __________  __________  __________
   1      2     ___   _________  __________  __________  __________  __________  __________
   1     inf    ___   _________  __________  __________  __________  __________  __________

   2      1     ___   _________  __________  __________  __________  __________  __________
   2      2     ___   _________  __________  __________  __________  __________  __________
   2     inf    ___   _________  __________  __________  __________  __________  __________

  inf     1     ___   _________  __________  __________  __________  __________  __________
  inf     2     ___   _________  __________  __________  __________  __________  __________
  inf    inf    ___   _________  __________  __________  __________  __________  __________

 'fro'    1     ___   _________  __________  __________  __________  __________  __________
 'fro'    2     ___   _________  __________  __________  __________  __________  __________
 'fro'   inf    ___   _________  __________  __________  __________  __________  __________

More on the Spectral Radius

In the above text there is a statement that the spectral radius is not vector-bound with any norm, but that it ``almost'' is. In this section we will see by example what this means.

In the first place, let's try to see why it isn't vector-bound to the norm. Consider the following false ``proof''. Given a matrix , for any vector $\bf x$ , break it into a sum of eigenvectors of as

$\displaystyle {\bf x}=\sum x_i{\bf e}_i$

where ${\bf e}_i$ are the eigenvectors of

, normalized to unit length. Then, for $\lambda_i$ the eigenvalues of

$\displaystyle \Vert A{\bf x}\Vert^2_2$	$\displaystyle =$	$\displaystyle \Vert\sum \lambda_i x_i{\bf e}_i\Vert^2_2$
	$\displaystyle \leq$	$\displaystyle \max_i \vert\lambda_i\vert^2\sum \vert x_i\vert^2$
	$\displaystyle \leq$	$\displaystyle \rho(A)^2\Vert{\bf x}\Vert^2$

and taking square roots completes the ``false proof.''

Why is this ``proof'' false? The error is in the statement that all vectors can be expanded as sums of orthonormal eigenvectors. If you knew, for example, that were positive definite and symmetric, then, the eigenvectors of would form an orthonormal basis and the proof would be correct. Hence the term ``almost.'' On the other hand, this observation provides the counterexample.

Exercise 3: Consider the following (nonsymmetric) matrix

A=[0.5  1   0   0   0   0   0 
    0  0.5  1   0   0   0   0 
    0   0  0.5  1   0   0   0 
    0   0   0  0.5  1   0   0
    0   0   0   0  0.5  1   0
    0   0   0   0   0  0.5  1
    0   0   0   0   0   0  0.5]

You should recognize this as a Jordan block. Any matrix can be decomposed into several such blocks by a change of basis.

Use the Matlab routine [V,D]=eig(A) (recall that the notation [V,D]= is the way that Matlab denotes that the function--eig in this case--returns two quantities) to get the eigenvalues (diagonal entries of D) and eigenvectors (columns of V) of A. How many linearly independent eigenvectors are there?
You just computed the eigenvalues of A. What is the spectral radius of A?
For the vector x=[1;1;1;1;1;1;1], what are $\Vert{\bf x}\Vert _{2}$ , $\Vert A{\bf x}\Vert _{2}$ , and $(\rho(A))(\Vert{\bf x}\Vert _{2})$ ?
For this case, is $\Vert Ax\Vert _2\leq\rho(A)\Vert x\Vert _2$ ?

It is a well-known fact that if the spectral radius of a matrix A is smaller than 1.0 then $\lim_{n\rightarrow\infty} A^n=0$ .

Exercise 4:

For x=[1;1;1;1;1;1;1] compute and plot $\Vert A^kx\Vert _{2}$ for $k=0,1,\dots,40$ . Please include this plot with your summary.
What is the smallest value of for which $\Vert A^kx\Vert _{2}\le\Vert Ax\Vert _{2}$ ?
What is $\max_{0\le k\le40} \Vert A^kx\Vert _{2}$ ?

The Euclidean norm (two norm) for matrices is a natural norm to use, but it has the disadvantage of requiring more computation time than the other norms. However, the two norm is compatible with the Frobenius norm, so when computation time is an issue, the Frobenius norm should be used instead of the two norm.

The two norm of a matrix is computed in Matlab as the largest singular value of the matrix. (See Quarteroni, Sacco, Saleri, p. 17-18, or a Wikipedia article http://en.wikipedia.org/wiki/Singular_value_decomposition for a discussion of singular values of a matrix.) We will visit singular values again in Lab 9 and you will see some methods for computing the singular values of a matrix. You will see in the following exercise that computing the singular value of a large matrix can take a considerable amount of time.

Matlab provides a ``stopwatch'' timer that measures elapsed time for a command. The command tic starts the stopwatch and the command toc prints (or returns) the time elapsed since the tic command. When using these commands, you must take care not to type them individually on different lines since then you would be measuring your own typing speed.

Exercise 5:

You have encountered the magic command earlier. It generates a ``magic square'' matrix. A magic square of size contains the integers . Compute the magic square of size 1000 with the command
```
A=magic(1000);  % DO NOT LEAVE THE SEMICOLON OUT!
```
Use the command
```
tic;x=norm(A);toc
```
to discover how long it takes to compute the two norm of A. (Be patient, this computation may take a while.) Please include both the value of x and the elapsed time in your summary. (You may be interested to note that x = sum(diag(A)) = trace(A) = norm(A,1) = norm(A,inf).)
How long does it take to compute the Frobenius norm of A?
Which takes longer, the two norm or Frobenius norm?

Types of Errors

A natural assumption to make is that the term ``error'' refers always to the difference between the computed and exact ``answers.'' We are going to have to discuss several kinds of error, so let's refer to this first error as ``solution error'' or ``forward error.'' Suppose we want to solve a linear system of the form $A{\bf x}={\bf b}$ , (with exact solution $\bf x$ ) and we computed ${\bf x}_{\mbox{approx}}$ . We define the solution error as $\Vert {\bf x}_{\mbox{approx}} - {\bf x} \Vert$ .

Usually the solution error cannot be computed, and we would like a substitute whose behavior is acceptably close to that of the solution error. One example would be during an iterative solution process where we would like to monitor the progress of the iteration but we do not yet have the solution and cannot compute the solution error. In this case, we are interested in the ``residual error'' or ``backward error,'' which is defined by $\Vert A {\bf x}_{\mbox{approx}} - {\bf b} \Vert = \Vert {\bf b}_{\mbox{approx}} - {\bf b} \Vert$ where, for convenience, we have defined the variable ${\bf b}_{\mbox{approx}}$ to equal $A{\bf x}_{\mbox{approx}}$ . Another way of looking at the residual error is to see that it's telling us the difference between the right hand side that would ``work'' for ${\bf x}_{\mbox{approx}}$ versus the right hand side we have.

If we think of the right hand side as being a target, and our solution procedure as determining how we should aim an arrow so that we hit this target, then

The solution error is telling us how badly we aimed our arrow;
The residual error is telling us how much we would have to move the target in order for our badly aimed arrow to be a bullseye.

There are problems for which the solution error is huge and the residual error tiny, and all the other possible combinations also occur.

Exercise 6: For each of the following cases, compute the Euclidean norm (two norm) of the solution error and residual error and characterize each as ``large'' or ``small.'' (For the purpose of this exercise, take ``large'' to mean greater than 1 and ``small'' to mean smaller than 0.01.) In each case, you must find the true solution first (Pay attention! In each case you can solve in your head for the true solution, xTrue.), then compare it with the approximate solution xApprox.

A=[1,1;1,(1-1.e-12)], b=[0;0], xApprox=[1;-1]
A=[1,1;1,(1-1.e-12)], b=[1;1], xApprox=[1.00001;0]
A=[1,1;1,(1-1.e-12)], b=[1;1], xApprox=[100;100]
A=[1.e+12,-1.e+12;1,1], b=[0;2], xApprox=[1.001;1]

Case Residual large/small  xTrue   Error   large/small
 1   ________   _______   ______   _______   ________
 2   ________   _______   ______   _______   ________
 3   ________   _______   ______   _______   ________
 4   ________   _______   ______   _______   ________

The norms of the matrix and its inverse exert some limits on the relationship between the forward and backward errors. Assuming we have compatible norms:

$\displaystyle \Vert x_{\mbox{approx}} - x \Vert = \Vert A^{-1} A ( x_{\mbox{approx}} - x ) \Vert \le (\Vert A^{-1}\Vert) (\Vert b_{\mbox{approx}} - b \Vert )$

and

$\displaystyle \Vert A x_{\mbox{approx}} - b \Vert = \Vert A x_{\mbox{approx}} - A x \Vert \le (\Vert A \Vert)( \Vert x_{\mbox{approx}} - x \Vert )$

Put another way,

$\displaystyle ($ solution error $\displaystyle )$	$\displaystyle \le$	$\displaystyle \Vert A^{-1}\Vert ($ residual error $\displaystyle )$
$\displaystyle ($ residual error $\displaystyle )$	$\displaystyle \le$	$\displaystyle \Vert A \Vert($ solution error $\displaystyle )$

Relative error

It's often useful to consider the size of an error relative to the true quantity. This quantity is sometimes multiplied by 100 and expressed as a ``percentage.'' If the true solution is and we computed $x_{\mbox{approx}}=x+\Delta x$ , the relative solution error is defined as

$\displaystyle ($ relative solution error $\displaystyle )$	$\displaystyle =$	$\displaystyle \frac{ \Vert x_{\mbox{approx}} - x \Vert}{\Vert x \Vert}$
	$\displaystyle =$	$\displaystyle \frac{\Vert \Delta x \Vert}{\Vert x \Vert}$

Given the computed solution $x_{\mbox{approx}}$ , we know that it satifies the equation $Ax_{\mbox{approx}}=b_{\mbox{approx}}$ . If we write $b_{\mbox{approx}}=b+\Delta b$ , then we can define the relative residual error as:

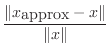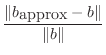$\displaystyle ($ relative residual error $\displaystyle )$	$\displaystyle =$	$\displaystyle \frac{\Vert b_{\mbox{approx}} - b \Vert}{\Vert b \Vert}$
	$\displaystyle =$	$\displaystyle \frac{\Vert \Delta b \Vert}{\Vert b \Vert}$

These quantities depend on the vector norm used, they cannot be defined in cases where the divisor is zero, and they are problematic when the divisor is small.

Actually, relative quantities are important beyond being ``easier to understand.'' Consider the boundary value problem (BVP) for the ordinary differential equation

$\displaystyle u''$	$\displaystyle =$	$\displaystyle -\frac{\pi^2}{100}\sin(\frac{\pi x}{10})$
$\displaystyle u(0)$	$\displaystyle =$	0	(2)
$\displaystyle u(5)$	$\displaystyle =$	$\displaystyle 1$

This problem has the exact solution $u=\sin(\pi x/10)$ . In the following exercise you will be computing the solution for various mesh sizes and using vector norms to compute the solution error. You will see why relative errors are most convenient for error computation.

Exercise 7:

Make a copy of your rope_bvp.m file from last lab. Change its name to bvp.m and modify it so that it corresponds to the boundary value problem in 2 above. This modification will involve setting , changing the values at the left and right boundaries, and changing the right side from a constant vector to one that varies as $\sin\frac{\pi x}{10}$ . Do not forget to change the comments. Note: In earlier sections, the vector $\mathbf{x}$ represented the unknown. Here, $\mathbf{u}$ represents the unknown (dependent variable) and $\mathbf{x}$ represents the independent variable.
As a test, solve the system for npts=10, plot the solution and compare it with sin(pi*x/10). You can use the following code to do so.
```
[x,u]=bvp(10);
plot(x,u,x,sin(pi*x/10));
legend('computed solution','exact solution');
```
The two solutions curves should lie almost on top of one another. You do not need to send me the plot.

Use code such as the following to compute solution errors for various mesh sizes, and fill in the following table. Recall that the exact solution is $\sin\pi x/10$ . (Note: you may want to put this code into a script m-file.)

sizes=[10 20 40 80 160 320 640];
for k=1:numel(sizes)
  [x,u]=bvp(sizes(k));
  error(k,1)=norm(u'-sin(pi*x/10));
  relative_error(k,1)=error(k,1)/norm(sin(pi*x/10));
end
disp([error(1:6)./error(2:7) ,  ...
      relative_error(1:6)./relative_error(2:7)])

                  Euclidean norm
          error ratio       relative error ratio
 10/ 20   ___________       ___________
 20/ 40   ___________       ___________
 40/ 80   ___________       ___________
 80/160   ___________       ___________
160/320   ___________       ___________
320/640   ___________       ___________

Repeat the above for the

vector norm.

                  1 vector norm
          error ratio       relative error ratio
 10/ 20   ___________       ___________
 20/ 40   ___________       ___________
 40/ 80   ___________       ___________
 80/160   ___________       ___________
160/320   ___________       ___________
320/640   ___________       ___________

Repeat the above for the $L^{\infty}$ vector norm.

                  Infinity vector norm
          error ratio       relative error ratio
 10/ 20   ___________       ___________
 20/ 40   ___________       ___________
 40/ 80   ___________       ___________
 80/160   ___________       ___________
160/320   ___________       ___________
320/640   ___________       ___________

The method used to solve this boundary value problem converges as . Since the number of mesh points is about , then doubling the number of mesh points should quarter the error. To see which of the above calculations yields this rate, fill in the following table with the words ``error'', ``relative error'' or ``both''.
```
                Rate=h^2?

Euclidean     ____________
one           ____________
infinity      ____________
```

As you will see, convergence rates are an important component of this course, and you can see it is almost always best to use relative errors in computing convergence rates of vector quantities. You may have noticed that relative norms have not been used in these labs, and the reason is, mainly, to avoid introducing an extra step into the computations.

The reason that the and norms give different results is that the dimension of the space, creeps into the calculation. For example, if a function is identically one, , then its norm, $\int_0^1\vert f(x)\vert^2dx$ is one, but if a vector of dimension has all components equal to one, then its norm is $\sqrt{n}$ . Taking relative norms eliminates the dependence on .

When you are doing your own research, you will have occasion to compare theoretical and computed convergence rates. When doing so, you may use tables such as those above. If you find that your computed convergence rates differ from the theoretical ones, before looking for some error in your theory, you should first check that you are using the correct norm!

A matrix example

It is a good idea to have several matrix examples at hand when you are thinking about some method. One excellent example a class of tridiagonal matrices that arise from second-order differential equations. You saw matrices of this class in the previous lab in the section on Discretizing a BVP. A $5\times5$ matrix in this class is given as

$\displaystyle A= \left(\begin{array}{rrrrr} 2 & -1 & 0& 0& 0 -1 & 2 & -1& 0& 0 0 & -1& 2& -1& 0 0 & 0 & -1& 2& -1 0 & 0 & 0 & -1& 2 \end{array}\right).$

(3)

More generally, the $N\times N$ matrix

has components $a_{kj}$ given as

$\displaystyle a_{kj}=\left\{ \begin{array}{ll} 2 & k=j -1 & k=j\pm1 0 & \vert k-j\vert\geq2 \end{array} \right.$

(4)

This matrix is tridiagonal (nonzero entries can be found only in three diagonals, the main diagonal and first superdiagonal and first subdiagonal). It turns out that the eigenvectors and eigenvalues of this matrix are well-known.

Exercise 8:

Consider a set of vectors, $\{\mathbf{v}^{(j)} \vert j=1,2,\ldots,N\}$ , each vector of which is -dimensional and has components $v^{(j)}_k$ given as

$\displaystyle v^{(j)}_k=\sin(j\pi\frac{k}{N+1}).$ (5)

Recalling that the ``sum of angles'' formula for $\sin$ is given as

$\displaystyle \sin(\theta+\phi)=\sin(\theta)\cos(\phi)+\cos(\theta)\sin(\phi)$

show by a direct (symbolic) calculation that $A\mathbf{v}^{(j)}=\lambda_j\mathbf{v}^{(j)}$ , and find the value $\lambda_j$ .
Note: Do this calculation by hand or use the Matlab symbolic toolbox or use Maple or another computer algebra program.
Hint: Choose one row of the vector equation $A\mathbf{v}^{(j)}=\lambda_j\mathbf{v}^{(j)}$ and insert the expressions (4) and (5) into the row equation. Simplifying should yield an expression for $\lambda_j$ . Please incude your calculation with your summary. If you did it by hand, type it in as best you can or use L^ATEX or scan it in and send me the file.

Complete the following Matlab function so that it generates the tridiagonal matrix A according to (4).

function A=tridiagonal(N)
% A=tridiagonal(N) generates the tridiagonal matrix A

% your name and the date

A=zeros(N);
??? code corresponding to equation (4) ???

Check that your code is correct by generating the tridiagonal matrix for N=5 and comparing with (3).
Test your hand calculation is correct by using Matlab to compute with and for the values j=1 and j=10, $\Vert A\mathbf{v}^{(j)}-\lambda_j\mathbf{v}^{(j)}\Vert _2$ .

Exercise 9: It may not be obvious from the eigenvalues you found in the previous exercise, but the determinant of the tridiagonal matrix A given in (4) is

. (Recall the determinant is the product of the eigenvalues.) In the case

, this can easily be seen by computing the determinant by ``row reduction.'' Starting from the original matrix, add

times the first row to the second to get

det $\displaystyle (A)=$ det $\displaystyle \left(\begin{array}{rrrrr} 2 & -1 & 0& 0& 0 -1 & 2 & -1& 0& 0 0 & -1& 2& -1& 0 0 & 0 & -1& 2& -1 0 & 0 & 0 & -1& 2 \end{array}\right) =$ det $\displaystyle \left(\begin{array}{rrrrr} 2 & -1 & 0& 0& 0 0 & \frac32 & -1& 0... ... 0 & -1& 2& -1& 0 0 & 0 & -1& 2& -1 0 & 0 & 0 & -1& 2 \end{array}\right).$

(6)

Next, adding

times the second row to the third gives

det $\displaystyle (A)=$ det $\displaystyle \left(\begin{array}{rrrrr} 2 & -1 & 0& 0& 0 0 & \frac32 & -1& 0... ... & \frac43& -1& 0 0 & 0 & -1& 2& -1 0 & 0 & 0 & -1& 2 \end{array}\right).$

(7)

Continuing this process gives

det $\displaystyle (A)=$ det $\displaystyle \left(\begin{array}{rrrrr} 2 & -1 & 0& 0& 0 0 & \frac32 & -1& 0... ... -1& 0 0 & 0 & 0& \frac54& -1 0 & 0 & 0 & 0 & \frac65 \end{array}\right).$

(8)

Since the determinant of an upper triangular matrix is the product of the diagonals, the determinant of this matrix is 6. In the following steps, you will transform this process into a calculational ``proof.''

Complete the following Matlab function so that it performs one Row Reduction Step (rrs) of a matrix A for row j,

function A=rrs(A,j)
% A=rrs(A,j) performs one row reduction step for row j
% j must be between 2 and N

% your name and the date
N=size(A,1);
if (j<=1 | j>N)  % | means "or"
  j
  error('rrs: value of j must be between 2 and N');
end

factor=1/A(j-1,j-1);  % factor to multiply row (j-1) by

 ??? include code to multiply row (j-1) by factor and ???
 ??? add it to row (j).  Row (j-1) remains unchanged. ???

Check your work by comparing it with (6-8).

For N=25, use your tridiagonal.m code to generate the matrix A. Use the Matlab det function to compute its determinant.
Take one row reduction step using rrs.m with j=2. Using det, find the determinant of this matrix.
Using a Matlab script m-file, write a loop to continue the row reduction process until it is complete. Using det, has the determinant changed?
Use the Matlab function diag to extract the diagonal entries of your reduced matrix. Check that some of them are given by for row number . Use the Matlab prod command to compute the determinant as the product of the diagonal entries.

Extra credit: the determinant (8 points)

The Laplace rule for computing the determinant of an $N\times N$ matrix with entries $a_{kj}$ is given by

det $\displaystyle (A)=\left\{ \begin{array}{ll} a_{11} & N=1 [3pt] \sum_{j=1}^N a_{kj}\Delta_{kj} & N>1 \end{array}\right.$

(9)

where

is any fixed index, and $\Delta_{kj}=(-1)^{k+j}$ det $(A_{kj})$ and $A_{kj}$ is the $(N-1)\times(N-1)$ matrix whose entries are obtained from

but with all of row

and column

omitted. For example, if

$\displaystyle A=\left(\begin{array}{cccc} 1 & 2 & 3 &\textcolor{blue}{4} \tex... ... & \textcolor{blue}{12} 13& 14 & 15 & \textcolor{blue}{16} \end{array}\right)$

then $a_{24}=8$ and

$\displaystyle A_{24}= \left(\begin{array}{ccc} 1 & 2 & 3 9& 10 & 11 13& 14 & 15 \end{array}\right)$

Exercise 10:

Write a recursive Matlab function compute the determinant of an arbitrary matrix A. Use your function to compute the determinant of the matrix A=magic(5) and check that your value of the determinant agrees with the one from the Matlab det function.
This is an extremely inefficient way to compute a determinant. The time taken by this algorithm is , a very large value. Time the computations of the determinants of magic(7), magic(8), magic(9) and magic(10), calling them , , , and $T_{10}$ . Show that $T_8\approx 8T_7$ , $T_9\approx 9T_8$ and $T_{10}\approx 10T_9$ , confirming the estimate.

Back to MATH2071 page.

kimwong 2019-02-25