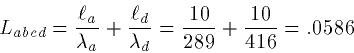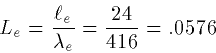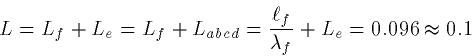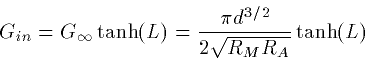

Next: Exploring transients in the
Up: Passive cell models
Previous: Solving boundary value problems
Recall that the input conductance for the semi-infinite cable is given
by:
Recall also that the space constant is
The electrotonic length of a cable of physical length, 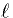 is
is
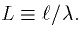 The input conductance at X=0 for a finite cable of
electrotonic length, L with a sealed end at X=L is just
The input conductance at X=0 for a finite cable of
electrotonic length, L with a sealed end at X=L is just
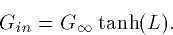
There are many other possibilities, but the sealed end is the most
common.
Figure 4:
Dendritic tree
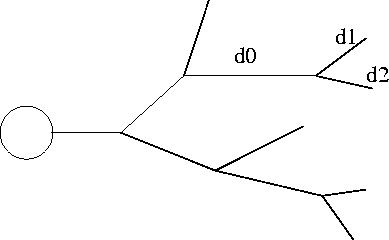 |
The idea that Rall discovered is that if the dendrites were related in
a particular fashion, then the whole thing could be collapsed to a
single cylindrical cable. This is called the equivalent
cylinder. Consider the tree shown in the figure 4. Suppose
that the branches, 0,1 and 2 have the same membrane resistivities,
RM and RA. Assume that the daughter branches, 1 and 2, have the
same electrotonic length, that is, their physical length divided by
their space constants (which of course depend on their diameters) are
all the same. (For example, if both have equal diameters and are the
same physical length.) Also, assume that the two have the same end
conditions, eg sealed. We want to know if it is possible to combine
the branches of the dendrite into a single equivalent cylinder. The
key is that we must avoid impedence mismatches. Thus, to combine the
dendrites, 1 and 2 with 0, we require:
- 1.
- All the ends are the same conditions, sealed.
- 2.
- The electrotonic lengths of 1 and 2 are the same
- 3.
- The diameters match as follows:
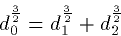
It is clear that this last condition is a consequence of the impedance
of the parent branch equalling that of the sum of the daughters. If
these conditions hold then 0,1,and 2 can be collapsed into a single
cylinder with diameter equal to that of dendrite 0 and total
electrotonic length as the sum of 1 and 0 (or equivalently 2 and 0.)
Example
Figure 5:
Example and exercise
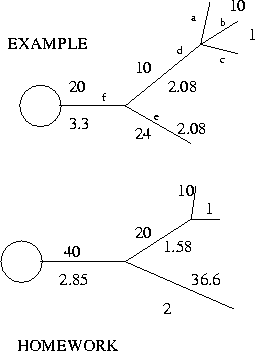 |
In the above figure, we depict a dendritic tree consisting of several
branches with their lengths and diameters in microns. (a) Can they be
reduced to an equivalent cylinder (b) What is the electrotonic length
(c) What is the input conductance. Assume sealed ends for all
terminal dendrites and assume that 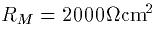 and
that
and
that 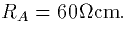
Answer.
da3/2 + db3/2+dc3/2 = 1+1+1 = 3 = 2.083/2=dd3/2
dd3/2+de3/2 = 3+3 = 6 = 3.33/2 = df3/2
so the 3/2 rule is obeyed. Clearly a,b,c are all the same
electrotonic length. The space constants are:
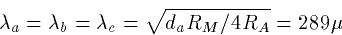
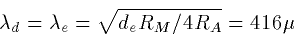
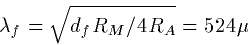
Thus, the total electrotonic length of abc with d is
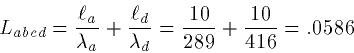
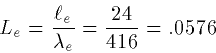
which are close enough to be considered equal (2% difference).
Thus, we can combine the whole thing into an equivalent cylinder. The
total electrotonic length is then:
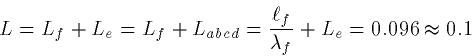
Finally, the input conductance is
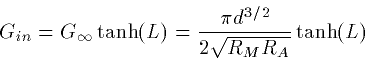
which is
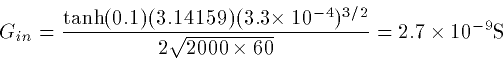
Exercise
Apply the same analysis to the bottom dendrite in
the figure.


Next: Exploring transients in the
Up: Passive cell models
Previous: Solving boundary value problems
G. Bard Ermentrout
1/10/1998
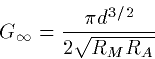
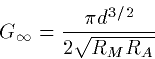
![]()
![]()
![]()
![]() and
that
and
that ![]()
![]()
![]()
![]()