

Next: Goldman-Hodgkin-Katz
Up: Ionic basis of the
Previous: Ionic basis of the
Each ion has an equilibrium potential associated with it whereby the
diffusive forces and the electrical forces balance. This is given by
the Nernst Equation
| ![\begin{displaymath}
E_i \equiv V_{in}-V_{out} = \frac{RT}{zF} \ln
\frac{[C]_{out}}{[C]_{in}}\end{displaymath}](img1.gif) |
(1) |
where T is the absolute temperature 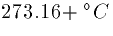 ,
,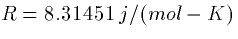 is the ideal gas constant,
is the ideal gas constant, 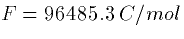 is Faraday's constant, and z is the valence of the
ion. Generally people use the logarithm base 10 in which case the
Nernst equation is multiplied by the factor 2.303. At
is Faraday's constant, and z is the valence of the
ion. Generally people use the logarithm base 10 in which case the
Nernst equation is multiplied by the factor 2.303. At
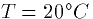 just multiply the logarithm base 10 of the ratio of
outside to inside by 58 mV to get the equilibrium potential. At
just multiply the logarithm base 10 of the ratio of
outside to inside by 58 mV to get the equilibrium potential. At
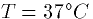 the multiplication factor is just 62 mV. The table at
the end of this section shows the typical equilibrium potentials for
various membranes at various temperatures.
the multiplication factor is just 62 mV. The table at
the end of this section shows the typical equilibrium potentials for
various membranes at various temperatures.
G. Bard Ermentrout
1/10/1998
![\begin{displaymath}
E_i \equiv V_{in}-V_{out} = \frac{RT}{zF} \ln
\frac{[C]_{out}}{[C]_{in}}\end{displaymath}](img1.gif)
![\begin{displaymath}
E_i \equiv V_{in}-V_{out} = \frac{RT}{zF} \ln
\frac{[C]_{out}}{[C]_{in}}\end{displaymath}](img1.gif)