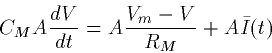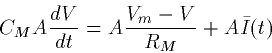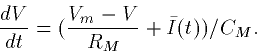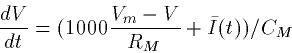

Next: Writing an ODE file
Up: Passive cell models
Previous: Electrical properties of a
Once we get beyond a single compartment model, it is much easier to
simulate the behavior rather than attempting to explicitly solve the
differential equations that you derive. In particular, once that are
more than 2 compartments and once channels and synapses are added,
simulation is just about the only generally applicable tool for
studying behavior. There are many simulation programs available and
we will talk about some of them later in the term; notably GENESIS and
NEURON, both of which are specifically designed for neural
simulations. Both of these simulators solve differential equations,
but their interface essentially removes the actual equations from you.
We will use a general purpose differential equation solver in
which we must explicitly provide the relevant equations. The
simulator is called XPPAUT and runs on any UNIX system with X
windows. A version that is similar but with some interface differences
is avaliable for Windows 95/NT.
The first model we will simulate is the single compartment injected by
a current (3)
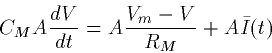
where A is the area of the membrane compartment. We can divide this
whole thing by A to get rid of it. We are interested in a
scale of millivolts, milliseconds and picoamps. Dividing by A CM
we obtain:
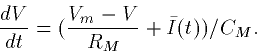
We use the following values for the parameters: 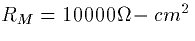 ,
,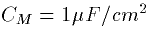 . The with units of milliseconds and millivolts, we
can set CM=1 and obtain:
. The with units of milliseconds and millivolts, we
can set CM=1 and obtain:
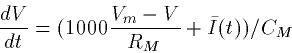
where 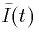 is measured in
is measured in 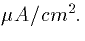 We can view the
reciprocal of the resistance as a conductance measured in
Siemens/cm2. The factor of 1000 comes from the conversion to
millivolts and from the factor of 10-6 from the capacitance. We
typically measure the conductance, gM=1/RM in
We can view the
reciprocal of the resistance as a conductance measured in
Siemens/cm2. The factor of 1000 comes from the conversion to
millivolts and from the factor of 10-6 from the capacitance. We
typically measure the conductance, gM=1/RM in 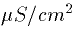 so that
we finally obtain:
so that
we finally obtain:
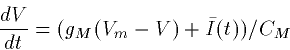
where gM=103/RM is the membrane conductance in 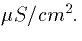 All units are now in terms of millivolts, milliseconds, and
microamps, microsiemens, microfarads per square centimeter.
All units are now in terms of millivolts, milliseconds, and
microamps, microsiemens, microfarads per square centimeter.


Next: Writing an ODE file
Up: Passive cell models
Previous: Electrical properties of a
G. Bard Ermentrout
1/10/1998