

Next: Numerical solution of passive
Up: Passive cell models
Previous: Ion concentrations and equilibrium
The simplest representation of a piece of nerve membrane is a simple
RC- circuit as shown in Figure 1. The capacitance of a
typical membrane, Cm arises due to the fact that there are layers of
conductive and nonconductive (lipids) media. The capacitance of a
typical patch of membrane is 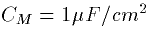 . That is the membrane
capacitance is measured in terms of the area of the membrane. The
larger the area, the larger the capacitance. Since we will be doing
most measurements in microns but most constants are in centimeters,
the conversion factor is 104 microns per centimeter. The actual
capacitance is then CMA where A is the area of the membrane
patch.
Thus, a spherical cell which
is 20 microns in diameter has a total capacitance of
. That is the membrane
capacitance is measured in terms of the area of the membrane. The
larger the area, the larger the capacitance. Since we will be doing
most measurements in microns but most constants are in centimeters,
the conversion factor is 104 microns per centimeter. The actual
capacitance is then CMA where A is the area of the membrane
patch.
Thus, a spherical cell which
is 20 microns in diameter has a total capacitance of
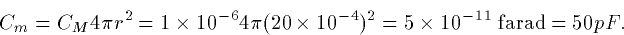
Figure 1:
Passive Membrane Model
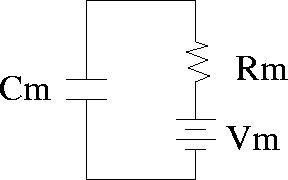 |
The membrane also has an associated resistance. As you might guess,
the smaller the patch of membrane, the larger is the resistance. The
resistance of a typical patch of membrane, RM is 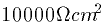 so that for our sphere, the actual resistance is Rm=RM/ A or
so that for our sphere, the actual resistance is Rm=RM/ A or
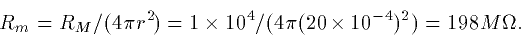
There are two main points to emphasize: (i) Associated with any
membrane are certain material constants that are independent of
the shape of the membrane, (ii) the actual electrical properties of a
membrane depend on its geometry.
We can now write the equation for a patch of membrane:
| 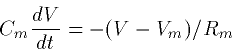 |
(3) |
which, if we multiply both sides by Rm obtain
| 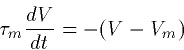 |
(4) |
where 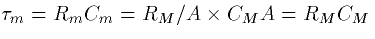 is called the membrane time constant.
It is independent of geometry. For our present choice of parameters,
is called the membrane time constant.
It is independent of geometry. For our present choice of parameters,
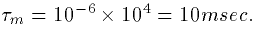 The true membrane resistance is
difficult to measure since electrodes will puncture the membrane and
thus decrease the apparent resistivity. This simple equation is called a
one-compartment model for a passive membrane. In general, as we will
see, all neural models are made up of pieces just like this and
ultimately so are connectionist models that can be derived from these
biophysical models. This is the EVE of GENESIS!
The true membrane resistance is
difficult to measure since electrodes will puncture the membrane and
thus decrease the apparent resistivity. This simple equation is called a
one-compartment model for a passive membrane. In general, as we will
see, all neural models are made up of pieces just like this and
ultimately so are connectionist models that can be derived from these
biophysical models. This is the EVE of GENESIS!
The solution to (4) is easy:
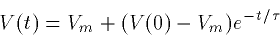
where V(0) is the initial voltage.
We could apply a steady current to this membrane as well. Typically,
currents are measured in terms of the area of membrane stimulated or
current density. The units are typically microamperes per centimeter.
This is convenient since one micro-farad times one milli-volt per one
milli-second gives
one micro-ampere. Positive currents are inward relative to the cell
and are called depolarizing while negative currents which are
outward relative to the cell are called hyperpolarizing.
Suppose we take Vm=-70mV and apply a step of
current to our spherical cell. Let's apply 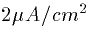 . What is the
voltage as a function of time?
The equation is
. What is the
voltage as a function of time?
The equation is
| 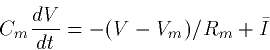 |
(5) |
whose solution is again easy to obtain if I is constant:
| 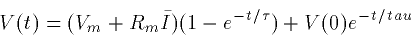 |
(6) |
Thus the voltage rises or falls to a new value dependent on the
current density. The current, 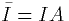 where I is the current
density. Note that the final value of the potential is dependent on
the current density and not the actual geometry of the cell since the
final potential is
where I is the current
density. Note that the final value of the potential is dependent on
the current density and not the actual geometry of the cell since the
final potential is 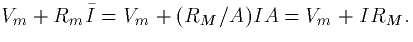 For
our present example, the steady state voltage is
For
our present example, the steady state voltage is
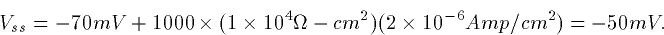
Note the factor of 1000 is necessary to convert to millivolts.
HOMEWORK
- 1.
- Calculate Rm and Cm for a cylindrical cell with diameter
of 10 microns and length of 50 microns. Ignore the area at the ends
of the cylinder.
- 2.
- How much current is needed to raise the potential to -55 mV in
the spherical cell example above?
- 3.
- Suppose that RM is
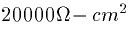 . What is the time
constant of the membrane.
. What is the time
constant of the membrane.
- 4.
- Suppose that the spherical cell above is initially at rest. Write the
equation for the voltage as a function of time if the current is stepped up to
10
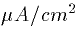 for 20 msec and then set to 0 again. (HINT: Use
(6) twice, once for the time when the stimulus is on.
Then again, using the voltage at the end of the stimulus as initial
voltage.) Sketch the voltage response to this current pulse.
for 20 msec and then set to 0 again. (HINT: Use
(6) twice, once for the time when the stimulus is on.
Then again, using the voltage at the end of the stimulus as initial
voltage.) Sketch the voltage response to this current pulse.


Next: Numerical solution of passive
Up: Passive cell models
Previous: Ion concentrations and equilibrium
G. Bard Ermentrout
1/10/1998
![]()
![]() so that for our sphere, the actual resistance is Rm=RM/ A or
so that for our sphere, the actual resistance is Rm=RM/ A or
![]()
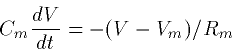
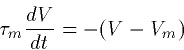
![]()
![]() . What is the
voltage as a function of time?
The equation is
. What is the
voltage as a function of time?
The equation is
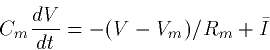
![]()