Synapses in a network setting

The above exercises illustrate the different effects of synapses and how they sum in concert with each other. However, the main reason for synapses is for neurons to communicate with each other within networks. One of the big theoretical and experimental interests of the last several years is the behavior of networks of neurons which oscillate and whether or not they synchronize. This interest arose due to some theoretical ideas by Christof von der Malsberg in the late 70's and early 80's. He was interested in how multiple aspects of a visual image such as color, texture, etc could be ``bound'' together to form a coherent whole. How can you seperate an figure from the background? He came up with the idea that oscillatory neurons could use phase information (that is the timing between the firing of the cells) to encode features of an object. All the cells that fire synchronously would correspond to the same object. The theory was viewed with great excitement when in the late 80's and early 90's Singer and Gray discovered that some cortical neurons would fire together synchronously over long distances in the cortex when presented with a continuous bar. If the bar was broken into two smaller bars, then the cells would fire but not synchronously. This spawned an industry of theory and experiment in synchronization of cortical oscillators. The firing rates of the cells during stimulation is around 40 Hz and this is called ``gamma'' rhythm. Thus, one of the major theoretical questions that has been asked is what kind of synaptic interactions lead to synchrony in networks of cortical and thalamic cells. In the following exercise, you will study a two-cell network of neurons coupled by synapses. The synapses are modeled by the first order dynamics above.

The ode file is :

# Two traub cells coupled together with synapses
# cell 1
v1'=-(gna*h1*m1^3*(v1-ena)+gk*n1^4*(v1-ek)+gl*(v1-el) -i1+gsyn2*s2*(v1-vsyn2))/c
m1'=am(v1)*(1-m1)-bm(v1)*m1
h1'=ah(v1)*(1-h1)-bh(v1)*h1
n1'=an(v1)*(1-n1)-bn(v1)*n1
s1'=alpha1*tmax*(1-s1)/(1+exp(-(v1-vt)/vs))-beta1*s1
# cell 2
v2'=-(gna*h2*m2^3*(v2-ena)+gk*n2^4*(v2-ek)+gl*(v2-el) -i2+gsyn1*s1*(v2-vsyn1))/c
m2'=am(v2)*(1-m2)-bm(v2)*m2
h2'=ah(v2)*(1-h2)-bh(v2)*h2
n2'=an(v2)*(1-n2)-bn(v2)*n2
s2'=alpha2*tmax*(1-s2)/(1+exp(-(v2-vt)/vs))-beta2*s2
am(v)=.32*(54+v)/(1-exp(-(v+54)/4))
bm(v)=.28*(v+27)/(exp((v+27)/5)-1)
ah(v)=.128*exp(-(50+v)/18)
bh(v)=4/(1+exp(-(v+27)/5))
an(v)=.032*(v+52)/(1-exp(-(v+52)/5))
bn(v)=.5*exp(-(57+v)/40)
par ek=-100,ena=50,el=-67
par gl=.1,gk=80,gna=100
par c=1,i1=0,i2=0,
par gsyn1=0,gsyn2=0,vsyn1=0,vsyn2=0
par vt=2,vs=5,tmax=3.2
par alpha1=1,beta1=.2,alpha2=1,beta2=.2
init v1=-67,v2=-67,h1=1,h2=1
@ dt=.25,meth=qualrk,total=100,xhi=100,ylo=-85,yhi=25
done

HOMEWORK The model is of two point neurons coupled together by first order synapses like we have already explored. The neurons are labeled 1 and 2 and neuron 1 synapses onto 2 with synapse s1 and maximal conductance gsyn1 and reversal potential vsyn1. Neuron 2 synapses onto neuron 1 with synapse s2 and maximal conductance gsyn2 and reversal potential vsyn2. The synaptic parameters, 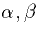$\alpha,\beta$ are alpha1, alpha2, beta1, beta2. Neuron 1 receives an applied current i1 and neuron 2 receives an applied current i2. Other than these parameters, the neurons are identical. Both neurons are at rest.

1.

Change the initial value of neuron 1 v1 from -67 to -60. This will cause the neuron to fire a pulse. Use the ``graphics'' ``add curve'' option to add the voltage of cell 2 (v2) to the plot. It should be flat. Increase the synaptic conductance gsyn1=.05 which impinges on cell2 from cell 1. Reintegrate the equations. Note that a spike occurs in both cell1 and cell2 since the firing of cell 1 depolarizes cell 2. Lower the conductance until there is no more spike. Observe a slight depolarization of cell 2 but no firing. What is the minimal conductance needed to elicit a spike? Now set gsyn1=.1, gsyn2=.1 Integrate the equations. What happens? Set both conductances to 0.15. Integrate the equations. What happens? Can you explain what is going on? What is the phase difference between the cells? Are they synchronized or not? Would this behavior happen if the cells were mutually inhibitory ? How about if one is excitatory and the other inhibitory?

2.

Now set i1=1,i2=1.05, gsyn1=.05,gsyn2=.05 and integrate the equations with mutual excitatory coupling. What sort of behavior is observed? To see the steady state behavior, you may want to integrate for a longer period of time.

3.

Make cell 2 inhibitory by changing vsyn2=-80. Change i1=.5, i2=0, gsyn1=.1,gsyn2=.2 Integrate for 400 msec. Calculate the period of the oscillation. Change the decay rate of the inhibitory synapse (beta2=.1 and recalculate the period. Also do the same thing for beta2=.05. Explain why the period is getting longer.

4.

Here is a last example of the complexities of network behavior. Set vsyn1=0, vsyn2=-80, alpha2=.5,beta2=.01, gsyn1=.01 gsyn2=1, i1=3,i2=0. Set the total integration time to 1000. Integrate the equations. What do you see? Explain the behavior. How would you modify gsyn1 to get fewer cell 1 spikes per cell 2 spike? How would you get more cell 1 spikes per cell 2 spike?

This exercise should give you an appreciation of how complex even simple networks can get. Synapses provide a powerful computational tool for sculpting complex behaviors out of simple networks. You can now imagine how complex behavior can be when all of the channels that we have previously described are added to the network. The fact that such models are tremendously complex and that solving these ``detailed'' (not really as far as the real biology is concerned) models is computationally expensive makes one ask how can one distinguish between models and how useful can these methods be? For this, reason, in the next set of lectures, we will look at simplified versions of these models and their computational properties.