The action potential

We have now derived the fundamental models for cables and active membranes and thus should be able to produce models of individual neurons and banched neuronal structures such as dendrites and axons. Networks of neurons communicate in a variety of means but by far the most common is through synapses. Synapses are exceeding complex and involve a large number of biochemical steps, can be modified and modulated by external substances, and are capable of undergoing slow adaptation and facilitation. Nevertheless, we will blunder on in order to describe ways in which one might model them; for without synapse, we cannot model networks and without networks, we are nothing. Indeed, to paraphrase Dorothy Parker, you can put a cell in culture but you can't make it think. The first step in this process of communication is the action potential; abbreviated as ``AP.'' The action potential occurs when we combine the active membrane theory of ``channeling'' with the passive cable theory. The compartmental model is then:

$$C_m \pi l d \frac{dV_j}{dt} + I_{act}\pi ld = \frac{\pi (d/2)^2}{R_a l}(V_{j+1}-2V_j+V_{j-1})$$

where I_act contains all of the active channels with conductances given in terms of density per unit area and l is the length of the compartment and d is the diameter of the cylinder. Dividing by $\pi ld$ and letting $l\to 0$ to approximate a continuous axon, we obtain:

$$C_m \frac{\partial V_j}{dt} + I_{act} = \frac{d}{4R_a}\frac{\partial^2V}{\partial x^2}$$

which is the model for the continuous axon originally modeled by HH. One can numerically simulate this partial differential equation and it is found that for each set of parameters, there is a solution that is a travelling wave. That is, there is a solution that keeps the same spatial profile translated in time. Specifically, V(x,t)=U(x-ct) where U is a particular function and c is the velocity of the wave. (See illustration of the wave.) A natural question to ask is how does the velocity depend on say, the geometry or the coupling? This is easily seen from the above. The term d multiplies two spatial derivatives of V, thus, the velocity depends on d as the square-root. That is, quadrupling the diameter doubles the velocity. Similarly quadrupling the intra-axonal resistance halves the velocity. The rigorous existence of traveling waves to the HH equations was independently proven in the 70's by Stuart Hastings and Gail Carpenter.

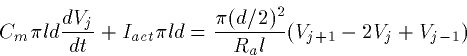
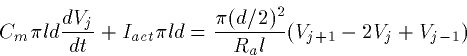
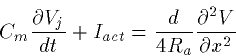
The AP provides the means of communicating between neurons by activating the axon and causing a signal to travel unattenuated down the cable. It is possible to block this by various means. For example, if the diameter of the axon increases drastically (say at a branch point) then the impuls can be blocked. Since there is no intrinsic anisotropy in the axon, it is possible to initiate an impulse any where and it will propagate outward (see Figure.) Because of the refractory period following the AP, the conducting medium behind the AP is very hyperpolarized and remains so until the sodium-potassium pump is able to rebalance the ionic concentrations. As a consequence of this, two propagating action potentials that collide, annihilate, unlike more common physical waves such as boles or light waves which pass through each other unchanged. (Note that for linear waves, this is a trivial observation, but for boles this requires some amount of mathematics.)

 

Figure 3: Voltage contour of an action potential in space-time

Repeated stimuli can have somewhat complicated effects. The simplest is to produce a train of waves that are equally spaced dowm the axon. If we let $\nu$ denote the velocity of the waves and T their period, then there is a relationship between $\nu$ and T called the dispersion relation. Any nonlinear medium capable of producing waves has such a relationship. You have probably observed it in water; waves with different magnitudes have different velocities and thus tend to disperse through the medium. Generally, the higher the temporal frequency, the smaller is the amplitude and velocity. The fastest wave is the one with zero frequency; the solitary pulse. The quantity, $1/(T\nu)$ has dimensions of 1/dist and is called the wavenumber or spatial frequency of the waves. Nonmonotone dispersion relations have profound consequences for the spacing of waves and it is possible to get doublets and other complicated spacings of impulses. The mathematical analysis of this type of phenomena has led to some striking insights into propagation of the lowly action potential.

In spite of all this interesting behavior, when it comes time to model networks of neurons, most people ignore it and model the action potential via a conduction delay. The range of velocities are from 2-10 meters/second for a typical impulse, the faster occuring in myelinated axons. In a small piece of cortical tissue a millimeter on the side, the maximum of these delays is less than a millisecond so that for purposes of modeling we will generally neglect them. However, in parts of the olfactory cortex, there appear to be instances where conduction delays are important.