

Next: GABAergic synapses
Up: Glutamate
Previous: AMPA/Kainate
An important receptor found in cortical
pyramidal neurons is the NMDA receptor. They are quite slow with rise
times of about 20 msec and decay times of 25 to 120 msec. A fairly
good simple model for NMDA is
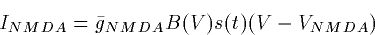
where s(t) obeys first order dynamics. There is an important
difference between NMDA and AMPA. The conductance depends in a complex
fashion on the postsynaptic potential via the term B(V). This
voltage dependent conductance depends on the level of external
magnesium ions. Here is a physiological
correlate of the Hebb rule that both pre- and postsynaptic cells must
be coincidently active. The voltage dependence is mediated by magnesium
ions which normally block the NMDA receptors. Thus, the postsynaptic
cell must be sufficiently depolarized to knock out the magnesium
ions. This is modeled in Jahr and Stevens, J. Neuroscience 10,
1830-1837:
![\begin{displaymath}
B(V) = \frac{1}{1+ e^{-.062V}[Mg^{2+}]/3.57}\end{displaymath}](img47.gif)
By
blocking the magnesium, it is possible to eliminate the voltage
dependence and measure the kinetic parameters. A simple first order
model is
![\begin{displaymath}
\frac{ds}{dt} = \alpha [T] (1-s) - \beta s\end{displaymath}](img30.gif)
as in the AMPA current, but , 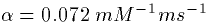 ,
,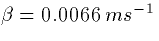 and
and
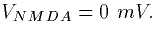
G. Bard Ermentrout
2/12/1998
![]()
![\begin{displaymath}
B(V) = \frac{1}{1+ e^{-.062V}[Mg^{2+}]/3.57}\end{displaymath}](img47.gif)
![\begin{displaymath}
\frac{ds}{dt} = \alpha [T] (1-s) - \beta s\end{displaymath}](img30.gif)