
| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Background reading: J. Schwartz and M. McGuinness, Einstein for Beginners. New York: Pantheon.. pp. 109 - 116.
Relativity theory tells us that a moving clock is slowed down and a moving rod is shrunk in the direction of its motion. If I am an inertial observer, I will find the effect to come about for the clocks and rods of a spaceship moving past at rapid speed. But if that spaceship is moving inertially, then, by the principle of relativity, the spaceship's observer must find the same thing for my clocks and rods. Relative to that observer, my clocks and rods move past at great speed. So that observer would find my clocks to be slowed and my rods to be shrunk in the direction of my motion.
Each finds the others clocks slowed and rods shrunk. How can both be possible? Is there an inconsistency in the theory? If I am bigger than you, then you must be smaller than me. You cannot also be bigger than me. That's the problem.
That each finds the others clocks slowed and rods shrunk is troubling. But is it a real paradox in the sense of there being a logical contradiction? If I walk away from you, simple perspective effects make it look to each of us that the other is getting smaller. I judge you to grow smaller; and you judge me to grow smaller. No one should think that this is a paradox.

That perspectival effect should not worry anyone. The car in the garage problem is an attempt to show that the relativistic effects are more serious than this simple perspectival effect. There is, it tries to show, a real contradiction; and we should not tolerate contradictions in a physical theory.
| Here is how we might try to get a contradiction
out of the relativistic effect of each observer judging the other to
have shrunk. Imagine a car that fits perfectly
into a garage. The garage is a small free standing shed that is just
as long as the car. There is a door at the right and a door at the
left of the garage. The car fits exactly--as long as it is at rest. |
Now image that we drive the car at 86.6% speed of light through the garage from right to left. The doors have been opened at the right and the left of the garage to allow passage of the car. There is a garage attendant, who stands at rest with respect to the garage. Can the garage attendant close both doors so that, at least for a few brief moments, the car is fully enclosed within the garage?
| According to the garage
attendant, there is no problem achieving this. At 86.6% the
speed of light, the car has shrunk to half of its length at rest. It
fits in the garage handily. The garage attendant can close both
doors and trap the car inside. |
According to the car driver, however, matters are quite different.The car is at rest and the garage moves. The garage approaches the car at 86.6% the speed of light. So the car driver finds that it is the garage and not the car that has shrunk to half its length. The garage is now half as long as the car. The car driver says that there is no way the garage attendant can shut both doors and trap the car fully inside. |
Now this is a serious problem. Either the car can or cannot be trapped fully within the garage, but not both. (Or so it would seem.)
| if you are interested in paradoxes, you might like to look at a text on paradoxes written for a companion course that covers just paradoxes of chance and infinity. It is written in a similar vein to this present text, Einstein for Everyone. | More formally, we have a true paradox. The term paradox has multiple meanings. It might just designate something that is unexpected in an amusing way; or something so unexpected as to be unbelievable. In its strongest form, it is the appearance of a logical contradiction in a system we thought free of contradiction. (We have such a contradiction when we can deduce both some proposition A and its negation not-A.) That seems to be what is happening here. We seem to be able to deduce both of: |
It IS the case that car is fully
trapped within the garage.
It IS NOT the case that the car is fully trapped within the garage.
It is usually taken to be a fatal problem when a theory is shown to harbor contradictions. I say "usually" since there are exceptions. We shall see later that, when quantum theory first emerged, it harbored a highly visible logical contradiction. Dealing with it was an urgent problem.
| There is a solution. It depends upon our remembering that that there is more in special relativity than the slowing of clocks and the shrinking of rods. We have already seen the relativity of simultaneity which will take on greater and greater importance in our assessment of the theory. It tells us that observers in relative motion can disagree on the timing of spatially separated events. | Note that an "event" in the context of relativity theory has a narrow meaning. It is something that happens at one place and at one time. Events are not spread out in space and time as might be the sort of events that we talk about in everyday talk. In relativity theory, an event happens at just one moment and one spot. |
The possibility of that disagreement is the key to the
problem of the car and the garage. A judgment of the simultaneity of
events is essential to any judgment of whether
the car was trapped in the garage by the closing of doors. The
car driver and the garage attendant disagree on whether the car is ever
fully enclosed in the garage simply because they disagree on the time
order of two events.
| The garage attendant says: There are two events: "Left door shut": I closed the left door before the car struck it. "Right door shut": I closed the right door after the car passed. And these events happened at the same time. Therefore the car was fully enclosed. |
|
|
|
The car driver says: "There are two events. "Left door shut": You closed the left door before the car struck it. "Right door shut": You closed the right door after the car passed. But these events did not happen at the same time. You closed the left door first. Then--later--you closed the right door after the front of the car had already burst through the closed left door. Therefore the car was never fully enclosed. To see this time order of the events, remember the rule from the preceding chapter. If two events are simultaneous in one inertial frame of reference, then they will not be so in another moving in the direction of the events. We have: • trailing event--earlier. • leading event--later. |
Both agree that the two events "left door shut" and "right
door shut" happened. They disagree on
the time order in which they happened. But that time order is
what is needed to decide whether the car was fully enclosed in the garage.
In a nutshell:
• The car can only be said to have been fully enclosed in the garage if
both doors were shut at the same time.
• There is no observer independent fact of the matter as to timing of
these events.
• Therefore there is no observer independent fact as to whether the car
was ever fully enclosed in the garage.
The problem of the car and the garage shows how judgments of lengths are entangled with judgments of simultaneity. This entanglement runs throughout special relativity. Indeed, one can understand all the odd kinematical effects as derived from it; for this reason, it was the first effect Einstein discussed in his 1905 paper.
For example, the relativity of simultaneity lies behind relativistic length contraction. To see this, consider how we might measure the length of a moving object. Take a car moving along a freeway at fancifully high speeds, so that relativistic effects come into play. I am standing by the roadside and want to know the car's length--or at least its length relative to me.
I cannot just hold up a measuring rod and proceed in the normal way: that is, check which marks on the rod align with each end of the car. For the car is zooming past. By the time I have noted the alignment of the front of the car with, say, the 0 mark on the measuring rod, the car has long since zoomed off into distance. I will have had no chance to check where the rear of car aligned. I need a more refined procedure.
Here's one: as the car zooms by, I stand with a friend at
the roadside, each of us holding a raised flag, ready to plant into the
roadside. As the front of the car passes, I plant my
flag into the roadside; as the rear of the car passes my friend,
my friend plants his flag into the roadside. The car zooms away. But that
doesn't matter anymore. I have the information I need in the locations of
the flags. I can use my measuring rod to determine the distance between
the flags. That is the length of the moving car.
What is essential to this procedure is that I and my
friend plant our flags at the same time.
Otherwise the distance between the two marks will not properly reflect the
length of the car.
But there's the catch. The car driver will disagree with my judgments of which events are simultaneous. The car driver will agree, of course, that there are two events, the planting of the two flags. But the car driver will not agree that I and my friend placed the marks simultaneously. Rather the car driver will find my friend and I to be rushing toward the car and the two flag plantings to have happened at different times. As the figure shows, the car driver will judge the planting of my flag at the front to have happened first; and the planting of my friend's flag at the rear to have happened later. Remember the rule: • trailing event--earlier. • leading event--later. |
Here's an animated version of this process.

Since my friend delayed the planting of the flag at the rear (in the car driver's judgment), the rear of the car advanced for some short time after I'd planted my flag at the front. Therefore (in the car driver's judgment) the distance we staked out with the flags is shorter than the length of the car and our determination of the length of the car is wrong. Hence we end up disagreeing about the length of the car.
The important point is that neither of us (driver and roadside observer) has made an error. There is no absolute fact as to which of us is really moving. Therefore there is no absolute fact as to which of our judgements of the timing of the two events is correct. Just as in the case of the car and the garage, we each judge the other as shrunken because we judge the simultaneity of events differently.
Similar considerations arise in judgments of the slowing of moving clocks. To see how the relativity of simultaneity underlies the relativistic slowing of clocks, we attend to a procedure we might use to measure the effect.
To judge the rate of a clock that passes me I need to be able to compare its reading with my wristwatch now and then compare its reading again later with my wristwatch after some time has passed. If the clock is running slow, I'll notice that its rate lags behind my wristwatch.
The catch in this simple procedure is that the clock is moving. I might find that both it and my wristwatch read the same time now, at the moment the clock passes. But the clock is moving rapidly. So after some time has elapsed, it has moved off into the distance.
How can I find out what the moving clock reads an hour from now when it is no longer anywhere near me? Here's one procedure: an observer sets up many clocks at rest with respect to a long platform that extends throughout space. Then, while a moving clock passes each one of those clocks, a friend notes what the moving clock reads and what the local resting clock reads; and so on for each of the clocks passed. From the friends' reports, the platform observer can figure out whether the moving clock has slowed or not.
The figure shows the bare essentials of the moving clock and all the other clocks spread out along the platform. The moving clock agrees with the "0" reading of the leftmost clock as it passes by. As it passes clocks successively along the platform, here's the list of reports the platform observers make:
When the moving clock reads "0," it is passing a clock
that reads "0."
When the moving clock reads "4," it is passing a clock that reads "8."
When the moving clock reads "8," it is passing a clock that reads "16."
When the moving clock reads "12," it is passing a clock that reads "24."
In short, the moving clock is found
to have slowed. It runs at half the speed of the clocks at rest
on the platform.
This procedure seems quite sound. So does that mean an observer
who travels with the moving clock would agree and judge the
moving clock to have slowed? No! We have seen that relativity theory
requires that observer to judge the platform array of clocks to be running
more slowly! How can that be?
By now you know the answer. An essential part of the procedure is that all the clocks laid out through space on the platform must be synchronized. A judgment of proper synchronization is a judgment of the simultaneity of events. Take the event at each clock when each of them reads "0." These must be simultaneous events. Otherwise the clocks will not be properly synchronized. The figure shows that, as far as the platform observer is concerned, the clocks are properly synchronized.
The relativity of simultaneity tells us that an observer moving with the clock will disagree with the platform observer on the relative timing of the events on the platform. Thus, if the platform observer judges the clocks on the platform to be properly synchronized, an observer moving with the moving clock will disagree: that observer will find them not to be properly synchronized. That moving observer will judge the platform clocks at the initial instant to have readings out of synchrony:
To see why they are out of synchrony in the way shown, recall the rule: "trailing event--earlier..." The reading of zero on the rightmost clock is the trailing event. It happens earlier than the reading of zero on the leftmost clock in the judgment of this new observer. After the earlier event in which it reads zero, the rightmost clock continues to tick and will have a reading larger than zero when the leftmost clock finally reads zero.
Let us now trace out the motions. The observer at rest with the clock finds the platform with its many unsynchronized clocks to move past it. To begin, the observer's clock reads zero when it coincides with the leftmost platform clock. When the platform has moved enough so that the observer's clock now coincides with the third leftmost platform clock, the observer's clock will have advanced in its reading from 0 to 4, whereas the third leftmost platform clock has advanced only from 6 to 8. That is the clock observer will judge this third leftmost platform clock to be running slowly, at half speed.
Similar judgments by the clock observer apply to the remaining platform
clocks. Here is how the successive instants will be judged to occur by an
observer who moves with the clock:
In short, the improper synchronization of the platform clocks fully explains to the moving observer how clocks on the platform, passed successively, show double the readings of the clock of the moving observer. The clocks on the trailing end of the platform have been set well ahead of those on the leading edge. Otherwise, everything proceeds as the moving observer expects. The clocks on the moving platform actually run at half the speed of the observer's clock.
As before, there is no absolute fact as to whether the clocks are properly synchronized. Therefore there is no absolute fact as to whether the moving clock slows with respect to the platform clocks; or whether the platform clocks slow with respect to the moving clock.
Once you recognize how fully the relativity of simultaneity is bound up in the relativistic length contraction and clock slowing effects, it is easy to fall into a new misunderstanding. One might think that the effects are not really part of the world at all, but that they somehow come about solely because of the way we set our clocks.
An analogy: it is possible to board a transpacific flight in Sydney, Australia, on one day and, after 16 hours of travel, disembark in Los Angeles the day before! Is this time travel? Of course not. During the flight, you crossed the international date line. That the calendar reads a day earlier in Los Angeles is purely an artefact of how we set our clocks and calendars across the world.
   http://en.wikipedia.org/wiki/File:Qantas_a380_vh-oqa_takeoff_heathrow_arp.jpg |
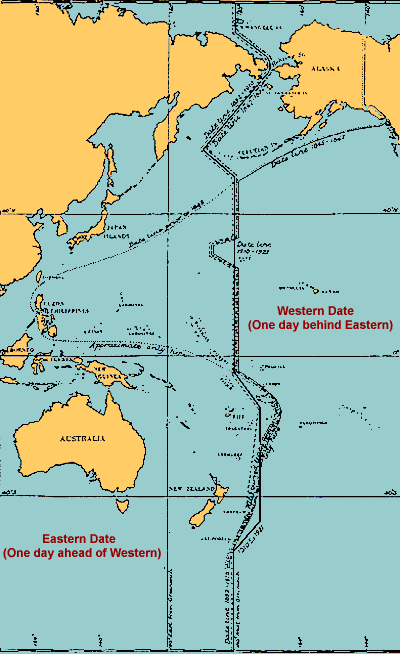 http://aa.usno.navy.mil/faq/docs/international_date.php Historical positions of the International Date Line from "Notes on the History of the Date or Calendar Line," in The New Zealand Journal of Science and Technology, Vol. XI, pp. 385 - 388 |
| In the early 1910s, this issue entered the
physics literature in discussion of the geometry of a rotating disk.
in 1911, Vladimir Varicak offered the following diagnosis of the
origin of relativistic length contraction: It "is only an illusory, subjective appearance, caused by the manner of our regulation of clocks and measurement of length" and "a psychological and not physical effect." |
 The rotating disk has some odd properties. Its circumference is relativistically contracted but its radius is not, resulting in "Ehrenfest's paradox." But this is a topic for another time. |
 |
Einstein's reply of the same year read: "The question of whether the Lorentz contraction really exists or not is misleading. ...[it is] not real in so far as it does not exist for a co-moving observer. ...[it is] real in so far as it can be demonstrated in principle by physical means by an observer that is not co-moving" |
| Einstein's paper is remarkably short. It is: Albert Einstein, "Zum Ehrenfestschen Paradoxon," Physikalische Zeitschrift, 12 (1911), pp. 509-510. Here it is, in its original German: |
For a careful overview of this debate between Einstein and Varicak and for the larger context, see Marco Giovanelli, "Appearance and reality: Einstein and the early debate on the reality of length contraction," European Journal for Philosophy of Science, 13, 2023. |


Here's an English
translation.
Einstein's reply is terse. What I think he is getting at is this. He is accusing Varicak of conflating two distinctions:
| Real versus unreal |
Observer
independent
versus observer dependent |
||
| That we age is real. That we travel backwards in time when flying from Sydney to Los Angeles is unreal. | That an object spins on it axis is observer independent; it is verified by the presence of inertial forces. That an asteroid moves uniformly in space must be judged relative to another object. |
What Varicak supposes is that being real goes with being observer independent; and that being unreal goes with being observer dependent. Hence, when we find an observer dependent effect, we have found an unreal effect.
Einstein's response is that we should decouple the two distinctions. That an effect is observer dependent does not determine whether it is real or not.
The simplest way to see how this works is to consider an asteroid rapidly approaching us. That it is moving rapidly is an observer dependent effect. For an observer on the asteroid, the asteroid is at rest. The effect is observer dependent, but the motion of the asteroid is very real for us. The reality, we might say, exists in the relation itself between our frame of reference and the asteroid.

Images: Asteroid:
https://www.nasa.gov/sites/default/files/thumbnails/image/edu_asteroid_large.jpg
Star field:
https://www.nasa.gov/sites/default/files/thumbnails/image/potw1703a.jpg
We should view relativistic length contraction in the same way. As the asteroid speeds past Earth--a fortunate near miss--we judge its length to be shortened. It is an observer dependent effect since it is not shared by another observer on the asteroid. However the contraction of its length is still a real effect.
Some observer dependent effects will be real; others will be unreal. What complicates our separation of the two cases is that changes in the observer's measurement procedures will create corresponding changes in the effect. We can use this complication to our advantage. We separate the real from the unreal by checking whether changes in the observer's procedures can eradicate the effect or not.
Recall the appearance of time travel that arises when one flies across the Pacific Ocean and crosses the international date line. The appearance of time travel everywhere can be eradicated merely by setting our world clocks differently. If clocks in Sydney and Los Angeles are set to read the international standard of Greenwich time, then the arrival in Los Angeles would always come later than the departure. There would be no appearance of time travel for any flight anywhere in the world. Thus the effect is unreal.
https://commons.wikimedia.org/wiki/File:US-Timezones.svg
public domain
Take the case of the relativistic slowing of clocks. Recall the earlier arrangement. A rapidly moving clock is judged to have slowed since it is found to show earlier times than the clocks it passes of the inertial frame of reference from which the effect is judged. We can eradicate the effect merely by introducing a non-standard synchronization of those frame clocks so that they agree with the readings of the rapidly moving clock as it passes each of them.
| The slowing will be eradicated for this
particular clock. But what of others? That's the catch. The slowing
effect will not be eliminated for all
clocks. Take a clock moving rapidly in the opposite direction at the
same speed, where its speed is judged by the original
synchronization of the frame clocks. It will be judged to slow at
twice the rate of the original unconfounded effect. This clock slowing effect is a real effect. It is manifested to an observer in an inertial frame by means of the clocks the observer has arranged through the frame. The mode of synchronization of those clocks will alter how the rate of slowing manifests. But the effect is not produced by the synchronization. For it cannot be removed completely by altering the mode of synchronization. We may eradicate it for one motion, but it comes back with greater strength for another. It is always there, even if in an obscured or confounded form. |
You can see this just by thinking through how
clocks must be reset to eradicate the slowing of the first clock. A
faster way is to recall the "twin
effect," to be discussed in a later chapter. A clock that
moves away from us and returns to the same place will have slowed.
The twin effect is measured at one place and thus is unaffected by
how we might synchronize our clocks. We can eradicate the portion of
the slowing that appears on the outward leg by non-standard
synchronization of the frame clocks. But the total slowing must
still appear for the full journey if we are to preserve the twin
effect. Therefore there must be a double slowing on the return leg. The literature on the thesis of the conventionality of simultaneity has explored what happens if we adopt some of these non-standard synchrony rules. This is discussed in a later chapter that covers the conventionality of simultaneity. |
It is helpful to compare this with the corresponding problem in ordinary Newtonian physics. There, rapidly moving clocks do not slow. However we could set up the clocks of some frame so as to give the illusion of a slowing of rapidly moving clocks. There would be a corresponding speeding up of clocks moving in the other direction. We would affirm that the whole effect is just an illusion. For by setting the clocks back to their normal synchronizations, we would find the entire effect of the speeding up and slowing down of clocks to have been eradicated.
We saw above how Einstein argued that Varicak was mistaken in treating the contraction of moving rods as illusory. After he had made his point, Einstein sought to drive home the point with a thought experiment. It is given the final paragraph of Einstein's 1911 paper, whose English text is here.
It is an interesting exercise for us here to examine the thought experiment. At first glance, it looks like Einstein shows that the contraction of moving rods can be recovered without worrying about judgments of the simultaneity of events. But then a closer examination shows that those judgments are still there. They must be there since any judgment of the length of a moving rod in relativity is necessarily tied up with judgments of which events are simultaneous. It is good practice for us to see how to find these judgments.
The thought experiment involves two rods of the same length when at rest. The first has endpoints A'B' and the second endpoints A''B''. I will add a third rod AB of the same length, when at rest, for convenience of the exposition.
All the rods are aligned in what Einstein calls the direction of the "X-axis." The first two rods A'B' and A''B'' move inertially at equal, constant speed in opposite directions. They approach one another:
The motions are such that they pass over each other while aligned above the third rod AB that is at rest in some inertial frame of reference.
When the ends A' and A'' of the two rods coincide, a mark is made on the resting rod AB at the location A*. Similarly, when the ends B' and B'' of the two rods coincide, a mark is made on resting rod AB at the location B*.
| The length of the moving rods can then be determined in the frame of reference of the resting rod AB merely by measuring the distance between the marks. This measurement can be carried out at leisure in the inertial frame of reference of the rod AB. According to the theory of relativity, the distance A*B* will be less than the length of the rod AB. The measurement affirms that the moving rods have shrunk. | The figures have been drawn such that the rods have shrunk to half their rest length. That requires them to be moving at √3/2c = 0.866c or 86.6% the speed of light. |
What of the judgments of simultaneity? There has been no talk of clocks and no talk of the relative timing of events. That Einstein can still promise a positive affirmation of the contraction without such considerations is the rhetorical strength of the thought experiment.
Nonetheless, judgments of the simultaneity of events are still essential to the result.The shorter distance A*B* measures the length of the two moving rods only if the events of the placing of the marks at A* and B* are simultaneous.
The clever part of Einstein's thought experiment is that the symmetry of the arrangement assures that the two marking events must be simultaneous in the frame of reference of rod AB. The arrangement treats left and right in exactly the same way. Everything that happens on the left side has its exact counterpart on the right side. Might it be that the marking at A* happens earlier than that at B*? That cannot be, since there is no physical difference in the arrangement on the left where A* occurs to distinguish it from the right where the marking at B* occurs. There is no physical basis in the arrangement for any difference in the timing of the markings at A* and B*. They must happen at the same time.
This is the distinctive feature of Einstein's two-rod thought experiment. It secures the simultaneity of the two marking events at A* and B* without employing any clocks to determine the simultaneity of events.



Einstein's thought experiment is ingenious and gives a strong sense that the length contraction is real, just as Einstein intended it would. However the thought experiment has not eliminated the need for a judgement of the simultaneity of events as a part of the procedure for measuring the length of the moving rods. Rather it has just made the judgments of simultaneity of the inertial frame of reference of the resting rod AB seem to be natural.
"Natural" just means we find it comfortable to accept. What Einstein's thought experiment does not establish is that the events of the markings at A* and B* have any special claim to identifying a preferred criterion of simultaneity. To do that would be to violate the principle of relativity. The judgments of simultaneity of each of the inertial frames of the rods A'B' and A''B'' are equally good and differ from that of the inertial frame of the rod AB.
To see this difference, consider how the process is judged from the inertial frame of reference of the rod A''B''. An observer on the rod A''B'' would find the rod A'B' approaching at great speed from the left and also considerably contracted in length, compared to the rest length of the rod A''B''. The rod AB would also be approaching and also be contracted in accord with its speed:
First, the ends A' and A'' would coincide and a mark would be made on the rod AB' at A*:
A small amount of time would pass and then, later, the ends B' and B'' would coincide. A mark would be made on the rod AB at B*. In this frame of reference, the event of the markings at A* and B* are not simultaneous.
| The principle of relativity assures us that the judgments of simultaneity of the frame of reference of A''B'' are just as good as those of the frame of AB. That the two moving rods will be judged contracted in the inertial frame of reference AB does still depend on the judgments of simultaneity of that frame of reference. | If A'B' and A''B'' move at √3/2c = 0.866c with respect to AB, then a short calculation using the relativistic rule of composition of velocities shows that A'B' moves at (8/7)(√3/2)c = 0.98974c with respect to A''B'' and that it has contracted 1/7 its rest length. |