| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Linked document: Geodesics of Space Near the Sun
In the last chapter, we learned the barest elements of Einstein's general theory of relativity. We now need to understand what those elements entail for gravity. The first place to start is the most familiar, the gravitational effects arising near a massive object like our earth or sun. These were the first applications of Einstein's new theory.
Let us return to the most basic question of gravity in general relativity. Why, according to the theory, do things fall down? We can take the simple and familiar case of bodies above the surface of a big mass like the earth. Consider, for example, a stone hurled vertically. It will rise and, if not hurled too quickly, will slow to a halt and then fall back down again.
Why does it do this? Why doesn't a stone like this just hover in space above the earth? Or, if it has some initial upward velocity, why does it not just fly off into space? The answer given by general relativity was already described in the last chapter. It is because spacetime is curved and the spacetime trajectories of free bodies follow the straightest lines of this curved spacetime geometry. We can be a little more specific for the very weak gravitational effects in the vicinity of the earth. The only parts of the spacetime curvature that make any sensible difference are those in the space-time sheets. Curvature in the space-space sheets produces no easily observed effect in the vicinity of the earth. (There is more to say here and it will be said in the next section.)
If we consider the spacetime region above the surface of the earth, we can be more specific about the curvature of the space-time sheets. Very loosely speaking, it appears as a very slight slowing down of time the closer we get to the earth's surface. More briefly, time runs more slowly closer to the earth's surface.
| Merely saying that "time runs more slowly" is
dangerously vague. We should make the idea more concrete. A better
representation concerns clocks. If we had clocks suspended at
different altitudes above the surface of the earth, those closer to
the earth would run more slowly. The effect is minuscule. To see it,
compare a clock on the surface of the earth
with one in distant space. When the clock in distant space ticks one
second, the one on earth would tick by almost one second. It would
be behind by just 6.977 x 10-10 second; that is roughly
seventy billionth of a second. The spacetime diagram greatly exaggerates the magnitude of the slowing effect. It shows the world lines of clocks suspended at different altitudes above the earth. The numbers count off the ticks marked by the clocks. |
 You might imagine that this is a delay that is so tiny that it could not make a different to anything that matters to us. As it happens, it makes a difference to the "GPS" Global Positioning System that many of us use everyday through our cellphones. GPS depends on signals sent from satellites orbiting above the surface of the earth. Their proper functioning depends on the satellites having very accurate clocks. Throught the curvature of spacetime, their altitude above the surface of the earth is enough to produce a very slight difference in the rates of their clocks compared to the those on the surface of the earth. This very slight difference is big enough to require correction if the GPS satellite clocks are to be the basis of reliable position data. |
This very slight difference is enough to make a noticeable difference to bodies that are free to move above the earth's surface. We saw in an earlier chapter that free bodies in the Minkowski spacetime of special relativity move along timelike geodesics. These are just those trajectories in spacetime along which the greatest proper time elapses. (You will recall, that proper time elapsed is just the time elapsed as read by a clock that moves with the body.) The same is true in general relativity: free bodies move along timelike geodesics, but now they are the timelike geodesics of the curved spacetime.
Consider a spacetime diagram for the stone that was hurled vertically upwards and then fell back down to earth. It starts its trajectory at event A and ends at event B. If this was a Minkowski spacetime, the trajectory of greatest proper time would be the dashed line AC'B.
However in this curved spacetime, AC'B is not the trajectory of greatest elapsed proper time. If we displace the trajectory slightly to higher altitudes, we allow it to access regions of spacetime where clocks run faster. Hence a small vertical displacement to some new trajectory ACB will increase the proper time elapsed as the body moves from event A to event B. When ACB is correctly chosen, displacing the trajectory to still higher altitudes will not further increase the proper time elapsed. For, to access the still higher altitudes, the body must now move with greater velocity and then the time dilation effect of special relativity will reduce the proper time elapsed.
The trajectory ACB represents the balance of two effects that gives the maximum: the faster clock rates at higher altitudes versus the clock slowing due to the velocity dependent time dilation. It is the trajectory of greatest proper time elapsed. It is a timelike geodesic that can be followed by a free body above the surface of the earth.
The timelike geodesic ACB is the trajectory of a free body in spacetime. It corresponds with the motion in ordinary space of a stone, hurled vertically upwards at event A and then falling back to the same position in space at event B.
This analysis covers just one case of vertical motion: when the body has an initial upward velocity. What about other cases in which the body may start at rest or even with an initial downward motion? Differences in the initial velocity will lead to different trajectories. These cases can be treated merely by choosing pieces of the trajectory ACB.
For example, take the case of a body that is initially at rest above the surface of the earth. Its initial position and motion corresponds to the event C of the curve ACB. We recover how it will move just from the future trajectory of the curve ACB after event C. Its motion will correspond to the curve CB shown below. If we carry out a closer analysis, if the distance fallen in space is small, then rate at which the body falls will conform with Galileo's seventeenth century law of fall: the spatial distance fallen increases with the square of time elapsed.
These motions connect directly to geodesic deviation. In the last chapter, we inferred from the way bodies fall above the earth to the curvature of the spacetime sheets near the earth's surface. We can now invert the inference. Take the space-time sheet whose spatial dimension is directed vertically above the earth. We have a negative, variable curvature in that space-time sheet in the vicinity of the earth.
The figure below shows no geodesic deviation for timelike geodesics very far from the earth (shown in the right of the figure). Closer to the earth's surface, timelike geodesics diverge (shown on the left of the figure). They indicate negative curvature, while also capturing a motion of all towards the earth.
This analysis can be extended to more complicated cases, such as projectiles hurled across the surface of the earth, the moon orbiting around the the earth and the planets orbiting around the sun. We would recover almost exactly the familiar results of Newtonian physics: projectiles follow parabolic trajectories in space and moons and planets orbit in space along elliptical orbits.
What might be puzzling is how such a very tiny slowing of clocks can produce what seems like such a big effect above the surface of the earth. Throw a ball into the air so that it rises to a height of 16 feet and then falls back again. It will do this in just 2 seconds. That seems like a huge deflection from uniform, straight line motion.
Contrary to this familiar appearance, it is not a big effect at all--at least not on the scale of effects that can arise in general relativity. The key to seeing this smallness is to note that, in our ordinary assessments, we use different units in measuring temporal and spatial displacements. We say that over a time of 2 seconds, the ball was deflected by 16 feet. That seems like a huge deflection. This changes if we measure time and space in the same units. We can rescale the distance measurement to a time measurement that arises naturally in general relativity. To rescale 16 feet, we ask "How long does light take to cover 16 feet?" Since the speed of light is so large, it is no surprise that light traverses 16 feet in merely 0.00000001636 seconds. That is, 16 feet is 0.00000001636 light-seconds. Using comparable units, the deflection of the ball over its 2 second flight is now very small. If the figure below were drawn to scale, the deflection would be quite imperceptible.
|
| Nonetheless the effect is there. Einstein's theory does say that the geometry of space becomes curved in the vicinity of very massive objects. That is true for the space we know that is close to both the great masses of the earth and sun. However the deviation from flatness in these spaces is so slight that no ordinary measurement can detect it. |  |
For this reason, we believed for millennia that our space is exactly Euclidean, whereas it is only very nearly so. These effects are worth pursuing. While they are small in the weak gravity of the sun and earth, they become more pronounced as we approach bodies of more intense gravity or consider the enormous distances of cosmology. That the curvature is even there in small degree in our part of space is of great foundational importance. It shows that the old idea that space has to be Euclidean is wrong empirically.
To get a sense of just how close our local geometry is to Euclidean, let us estimate the disturbance to it due to the presence of the sun. Consider a huge circle around the sun that roughly coincides with our earth's orbit. Euclidean geometry tells us that the circumference of this circle is 2π x radius of the orbit.
| Imagine that we now approach the sun one mile at a time and draw a new circle centered on the sun at each step. The Euclidean result tells us that for each mile we come closer to the sun, the circumference of the circle is diminished by 2π miles. |
| That is the Euclidean result. Because of the presence of the sun, space around the sun is not exactly Euclidean. According to general relativity, for each mile that we come closer to the sun, the circle does not lose 2π miles in circumference; it loses only (0.99999999)x2π miles. |
What does this slight disturbance to the geometry of space do to the straight lines of the spatial geometry? It causes them to deviate slightly from what you would otherwise expect.
To see the effect, consider two points A and B in the vicinity of sun. We first imagine that space in the vicinity of the sun has a flat, Euclidean geometry. A straight line between them will be the line of shortest distance and would be configured something like this:
If we now replace the geometry of space around the sun with the geometry predicted by general relativity, there will be a change in the line of shortest distance between A and B. We can anticipate what that change will be. As we approach the sun, the circles surrounding the sun no longer shrink in circumference as quickly as Euclid expected. Thus a line from A to B can become slightly shorter if it follows circles slightly farther away from the sun. The effect is that a line, deflected slightly away from the sun, will now be the line of shortest distance between A and B in space. It will look something like this:
It takes a little more effort to see that just this is the
correction required when we replace the Euclidean geometry of space with
that required by general relativity. The details are in:
Appendix: Geodesics of Space Near the Sun
The deflection is extremely small. However, as we will see below, it turns out to be one of the earliest effects actually measured.
Beware: while this figure looks a little like the spacetime diagram for a body in free fall above the surface of the earth, they are not the same. The line AB here is in ordinary three-dimensional space.
These deflections can be related to geodesic deviation. Straight lines in space (not spacetime) in a region remote from the sun show no geodesic deviation. They are shown at the top of the figure below. Straight lines closer to the sun do diverge and manifest a negative, variable curvature. They are shown lower in the figure.
This representation of how the geometry of space is affected by the presence of the sun is quite adequate. It is limited to intrinsic curvature. However another representation is possible. We can capture the deviations from Euclidean flatness in the space through extrinsic curvature. To do it, we imagine that the surface lives in a higher dimensioned Euclidean space and that its intrinsic curvature comes about from its extrinsic curvature in that space. We will pursue this since it leads to one of the most familiar images associated with general relativity in the popular literature.

https://commons.wikimedia.org/wiki/File:GPB_circling_earth.jpg
public domain
To make things concrete, let us imagine that we will build a real model out of some flexible sheeting material whose extrinsic curvature will display the geometry of space around the sun.
To build the model, we take the largest circle and lay it down as a ring on a flat, Euclidean bench surface. We then move inward one unit distance in radius to the next circle. We lay down a second smaller ring with the appropriate circumference and connect the two by the flexible sheeting of the model. In the case of Euclidean geometry, the circumference of the second circle will be reduced 2π units of distance, matching the behavior of Euclidean circles on the table top. Thus it will lie flat on the table, to produce the two circles shown below. The two circles would be joined by a flat ring of the sheeting that comprises the model.
In the case of the non-Euclidean geometry, when we move inward one unit of distance, we arrive at a circle whose circumference has lost less than 2π units of distance. As a result, it will have a greater circumference than the circles of the table surface one unit of radius closer to the center. That means that it will not lie flat on the Euclidean surface of the table. If we tried to lie it flat on the table surface, we would have to crumple the sheeting connecting the two circles. Since we want to avoid crumpling the sheeting, we would have to let it pop up above the table, as shown below.
The effect is greatly exaggerated in the figure. The amount the surface would pop up would be undetectable, if it accurately modeled the deviations from Euclidean space in our part of space. However the qualitative effect is correct. If we were to model the geometry of space very close to a very massive body, then the effect would be more marked.
We continue building our model by adding more circles nearer the sun, connected by sheeting to the circles farther out. What would result is more popping out of the sheet, until we have a familiar funnel shape. It has a saddle-like curvature, distinctive of negative curvature, and becomes more curved the closer we come to the sun.. The figure below inverts the funnel in keeping with the standard presentation of the model in the literature.
The model is an embedding diagram of the geometry of space near our sun. That is, it recovers the intrinsic curvature of a two-dimensional sheet of space-space by the extrinsic curvature of a model surface bending into a higher dimensional, Euclidean space. The model captures an important geometrical fact about the space around our sun--that it is no longer exactly Euclidean. It is one of the most frequently built models in the context of general relativity.
However it is misleading in two ways.
First, since it is an embedding diagram, we should not be misled into assigning any physical reality to the higher dimensioned space in which the surface is modeled. It is introduced solely for our ease of visualization. In fact the diagram is a step backwards in that it is a return to the old way of visualizing curvature as a bending of a surface into a higher dimensioned space. While it might be a useful aid to visualization, it is factually false. There is, as far as we know, no higher dimensioned space into which the surface bends.
| Second, a common way of encapsulating Einstein's theory is to roll marbles across the model and suggest that gravitational attraction somehow comes from the resulting deflection of the marble's roll. From the discussion above, you can see why that is misleading. The gravitational deflection of ordinary objects falling in the vicinity of the sun is due to the curvature of the space-time sheets. What the model shows is the curvature of the space-space sheets and that curvature is so small as to have negligible effects on the motions of ordinary objects. | The model is often described as a rubber membrane model and the picture is of a massive object sitting on a rubber membrane distorts the membrane. Just about the only thing right in the rubber sheet model is that the surface of the membrane is similar to the surface of the embedding diagram. Almost everything else is misleading and has to be imagined away. There is no gravity outside the membrane, for example, pulling the mass down so it distorts the membrane. Most importantly, there is no curvature of the space-time sheets of spacetime represented, even though that curvature is responsible for the familiar gravitational effects. |
 |
 http://en.wikipedia.org/wiki/File:Spacetime_curvature.png |
 |
From the NASA website "100 Years of General Relativity."
https://asd.gsfc.nasa.gov/blueshift/index.php/2015/11/25/100-years-of-general-relativity/
"At its most basic, general
relativity is a way to describe gravity by attributing it to the curvature
of space-time that occurs in the presence of massive bodies. Massive
objects cause space-time to stretch. One way to think about it is to
imagine stretching a piece of fabric between a couple of people, and then
plunking down a softball in the middle. The ball will make a dent in the
cloth. Then if you roll a small ball across the fabric, it will seem to be
attracted to the softball, though it's really just following the dent in
the cloth. It's not a complete picture of how gravity and general
relativity work, but it's a good way to start to wrap your head around
Einstein’s theory."

One of the consequences of Einstein's theory will have special importance to us. Gravity is a curvature of spacetime that affects all free fall motions. Light propagating is one of those motions. So just as massive bodies like planets and comets are deflected toward the sun, so also is light.
One of the characteristics of a Minkowski spacetime and the more general spacetimes of Einstein's theory is that they have a light cone structure. It maps out the fastest trajectories for causal interactions. Since gravity affects light, gravity will also affect this causal structure. The effect of gravitation is to tip the light cones in the direction of the gravitational attraction.
This can have some very interesting consequences, such as new regions of spacetime causally isolated from our region. These arise in the theory of black holes and we will see more of them later.
Shortly after Einstein completed his theory, he announced three empirical tests that he believed established the theory. Two had yet to be done. They were: I. Mercury; II. Light Bending; and III. Red Shift.
According to Newton's theory, planets orbit the sun along elliptical paths. Here's a picture of the orbital motion according to Newton's theory; and an animation:
 |
Einstein's theory predicted the same, but added that the
axis of the ellipses of the planetary orbits would advance
very slightly. That means the axis would rotate slowly in the
same direction as the planet's motion. In Mercury's case, the advance
would be about 43 seconds of arc per century. This amount of advance is
really very small. To see this, note that there are 60 minutes in one
degree and 60 seconds in one minute. So 43 seconds of arc is very much
less than a single degree. It would be impossible to use a sharp pencil
and a big sheet of paper to draw two intersecting straight lines that
intersect at 43 seconds of arc. They would be so close that they would
appear like one line. Yet this is the extra advance Einstein's theory
predicts over the time of 100 years.
Here is a picture of this advance, with the size of the advance greatly
exaggerated, and an animation:
|
|
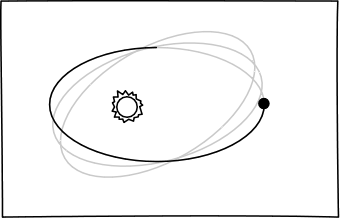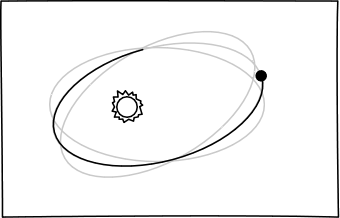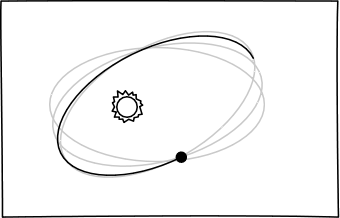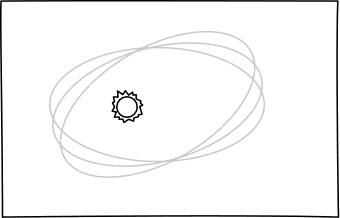 |
That so called "anomalous" advance had already been observed but no final explanation had been agreed on for it. When Einstein discovered that his theory predicted this elusive 43 seconds of arc, it might well have been the greatest scientific moment of his life. He recalled having heart palpitations, being unable to sleep and a sense that something inside snapped.
Of course the matter was more complicated than the above gloss suggests. Even in Newtonian theory, the ellipse of Mercury's orbit was expected to move by over 400 seconds per century due to the perturbations of the other planets. That means that the gravitational attraction of the other planets pulls Mercury off the simple elliptical orbit computed in their absence. Adding in the effects of these perturbations, Newtonian theory could account for all but about 40 seconds of the motion of the axis of Mercury's orbit. Until Einstein was able to explain it exactly with his general theory of relativity in late 1915, this small discrepancy did not seem to be very worrisome. It was only afterwards that explaining it became a sine qua non for any new gravitation theory.
Here's a contemporary account
from Simon Newcomb's authoritative The Elements of the Four Inner
Planets and the Fundamental Constants of Astronomy: Supplement to the
American Ephemeris and Nautical Almanax for 1897. Washington:
Government Printing Office, 1895, p. 184.

Note that Newcomb allows that the anomalous motion of Mercury could be accommodated if Newton's law of gravitation was not exactly an inverse square law. That is, he considers the possibility that the force of gravity does not dilute in inverse proportion with
(distance)2
but with
(distance)2.00000016120,
a supposition due to the astronomer Asaph Hall. We might wonder if this is an admission that no hypothesis within the existing system is expected to accommodate the anomaly so that an alteration of fundamental law has to be contemplated. Or, more likely, is it just a working astronomer noting the simplest way to develop a rule that will allow prediction of planetry motion?
Einstein's recovery of the anomalous motion of Mercury turned out to be a turning point in gravitational physics. Until Einstein's success, recovering precisely the anomalous motion was not regarded as an essential test of a theory of gravity. Prior to November 1915, gravitation theories could fail the test with impunity. In November 1915, that changed. From then on, if a new theory of gravitation was to be taken seriously, it had to match the performance of general relativity. It had to recover the anomalous motion of Mercury.
| Einstein's explanation of the anomalous motion of
Mercury has also exerted a strong influence in
philosophy of science. It was a striking achievement.
Einstein developed a theory of gravity using notions from then
obscure mathematics. There was no reason to expect that it would
recover Mercury's motion. There are no parameters that one can
adjust in the theory that would guarantee it. So when Einstein's
theory recovered the anomaly exactly, it was a powerful moment.
Philosophers of science have used it for a century as a wonderful
example of something done right. Just what that thing done right is
depends on which philosopher you ask. It might be an illustration of
how a good theory can be exposed to a severe test and pass. Or it
might show us how good explanations work: the anomaly in a motion is
now explained by a novel proposal for the character of gravity. For elaboration, see the later chapter,Philosophical Significance of General Relativity: Theory and Evidence: Novel Evidence and Adjustable Parameters. |
"No parameters to adjust"?
Hall tried to accommodate the anomalous motion of Mercury by
assuming that gravity does not dilute inversely with (distance)2.
Instead, he assumed it dilutes inversely with (distance) raised to
the power of some-other-number very close to two. It was a foregone
conclusion that there would be some-other-number close to two that
would do the job. It was really just a matter of tuning Newton's
inverse square law to recover whatever anomaly may come your way. If
the anomaly is bigger, you tune to it by selecting a power further
from two; it is small, you choose a power closer to two. What happened next? Hall's proposal disappeared quite quickly since it did not accommodated other, smaller anomalies in the motion of the other planets. |
| According to Einstein's theory, light, just like any other form of matter, is affected by gravity. That is, light also "falls" in a gravitational field. Just as a comet's trajectory is deflected by the sun when it passes nearby, a ray of starlight grazing the sun would also be deflected or bent. When we (or our camera) look at the star, we presume that the path taken by the light is straight. The effect of the bending of the light, then, is to make the star appear to be located in a slightly different position in the sky. | The effect is quite similar to a mirage in the desert. Light from a small patch of blue sky grazing the ground is deflected slightly upwards towards us. We look back along the lightray and misplace a small patch of blue sky as located on the ground. It looks like blue water. |
The deflection is measured as the change in apparent direction of the star from the earth; that is, it is measured as the angle between the direction in which we see the star and the direction in which we expected to see the star. Einstein computed that the deflection would be about 1.75 seconds of arc. This is a very tiny angle.There are 360 degrees in full circle. Each degree is divided into 60 minutes or arc and then each minute is further divided into 60 seconds of arc.
Measuring this tiny a deflection in the position of a star at the edge of the sun's fiery disk is quite difficult. It turns out that we must wait for an eclipse of the sun to block out the confounding effect of the dazzling light of the sun. After some failed attempts, an English expedition, headed by English astronomer Arthur Eddington, reported successful observation of the deflection for the solar eclipse of May 29, 1919.
Until then, Einstein had merely been a leading member of the physics community. The report of the success was picked up by the press and Einstein was launched as a famous public figure.
 One of Eddington's eclipse photos |
From the New York Times, November 10, 1919. Full article.  |
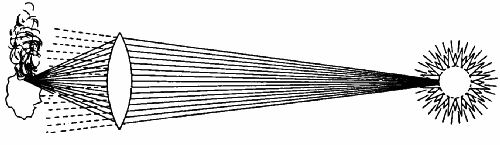
Curiously, the light bending effect turns out to be similar to one already expected in Newtonian gravitation theory. Under Newton's corpuscular theory, light consists of rapidly moving corpuscles with mass. As they propagate through space, they fall towards massive bodies like planets and stars. As a result, both the speed and direction of the light changes. In 1801, Johann Georg von Soldner had already computed the purely Newtonian effect of the deflection of starlight by the sun.
The figure shows the basic idea of the Newtonian calculation. The light from a distant star would normally propagate in a straight line in Euclidean space. However as the starlight propagates past the sun, it is pulled gravitationally towards it. The resulting fall bends the light ray away from the straight line of the Euclidean geometry of space. The amount of the deflection is measured as before by the change of angle for the apparent position of the star.
| General relativity allows for the same effect. A ray of starlight propagating past a massive body like the sun will also fall towards the sun. The amount of the fall is measured by the angular deflection of the star's apparent position and turns out to be the same deflection as predicted by Newtonian theory. | That it is the same--or at least so close that the difference does not matter--may seem surprising. It is really a familiar result. Instead of starlight, imagine a stone released from rest above the sun. In the first few moments of its fall, both Newton's and Einstein's theory must give us almost exactly the same result. For otherwise, the two theories would not agree on simple facts like the speeds of fall of bodies above the surface of the earth. While light propagating past the sun is moving very rapidly in the horizontal direction, the motion of fall in the vertical direction towards the sun is very small. The vertical fall is just like that of the stone. Both Newton's and Einstein's theories will agree on it. |
So far we have nothing new. What leads general relativity to make a different prediction from Newtonian theory is the geometric effect described above. Ordinary space in the vicinity of the sun has a slight curvature that leads to small deviations from Euclidean expectations. Light propagating near the sun will fall towards the sun, deviating from straight line motion. However the straight lines from which it deviates are themselves slightly bent. More precisely, they are bent in relation to what we would expect if the geometry of space around the sun were Euclidean.
The net effect is two bendings that are added together. First, straight lines are bent from Euclidean expectations; second, the rays of starlight are bent by the fall of the light towards the sun. It turns out that the angle of deflection of each of these effects is the same (and the same as the Newtonian angle of deflection). As a result, general relativity predicts a deflection of starlight that is twice as great as that predicted by Newtonian gravitation theory.
Early versions of Einstein's theory did not include the curvature of the geometry of ordinary space around the sun. This led to a close call in the testing of the theory.
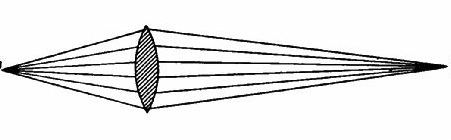
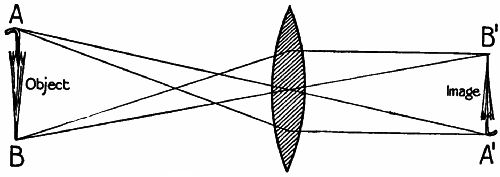
A minor variation on this effect arises if the deflecting body is massive enough to bring together the light that passes on either side of it from a luminous body behind it. Then the deflecting body acts a kind of lens, focusing the light. In the figure, the observer would see two images of the same object. In the case of perfect alignment, the observer would see a ring of duplicated images. This effect, known as "gravitational lensing," has only recently been observed. While Einstein did not discuss the effect in his publications, it turns out that he had computed it in a private notebook in 1913.
Here's a spectacular image of gravitational lensing:

Downloaded from http://hubblesite.org/newscenter/archive/releases/1995/14/image/a/format/web_print/ February 15, 2007.
The third empirical test announced by Einstein at the completion of his general theory of relativity was that light from the sun would be slightly reddened. This effect of this reddening follows directly from the effect described above of the slowing of clocks that are closer to a massive body.
Of course there are no ordinary clocks sitting on the surface of the sun for us to observe and see running slower than ours on earth. However, Einstein reasoned, there is something that might be even better. Heated atoms in the sun emit light of quite definite frequencies (and others absorb light of quite definite frequencies). The fixity of these frequencies is akin to the ticking of a very accurate clock. The emitted light is a wave with crests and troughs. Each emission of a peak is a "tick" of the atom's clock. In this sense, these atoms are better than ordinary clocks since their regularity is quite assured. Best of all, spectroscopists had become quite adept at measuring the frequencies of the light emitted by excited atoms.

Click
here for larger image.
Here is a spectrogram that splits light from the sun according to its
frequency and captures the spread photographically. Each vertical
line represents a different frequency. This spectrogram was taken
by Henry A. Rowland of Johns Hopkins University and published in 1886. It
is part of the collection of the National Museum of American History.
Source:
https://americanhistory.si.edu/collections/search/object/nmah_1184648
A slowing of these light emitting atom-clocks results in a slowing of the rate at which the atoms emit the peaks in the waveforms of the light. This slowing is a reduction in the frequency of the light. That means the light will be slightly reddened. When observers on earth see that reddening in their spectrograms, they are, in a sense, "seeing" the slowing of clocks on the surface of the sun.
This reddening was one of Einstein's very first predictions arising from his work on relativity and gravity. In his earliest paper on the subject of 1907, he had already predicted the gravitational slowing of clocks and had realized that this should manifest in a reduction (reddening) of the frequency of light from the sun by a mere 0.000002%, a two millionth part. It corresponds to the same percentage increase in the wavelength of the light.

From Einstein's 1907 paper. The highlighted
words say "about two millionth greater wavelength."
The spacetime diagram shows the processes in the effect. The world tube on the left is the sun. The lightlike worldlines propagating to the right trace the propagation of the peaks of the waveforms of the emitted light. The time intervals between the emissions of the peaks at the sun's surface is just the inverse of the frequency of the light, that is, its period. The peaks propagate to the world tube on the right, the earth. Clocks on the earth run slightly faster than those on the sun, by a two millionth part. So we earth observers find the time between the successive peaks to have been delayed by a two milllionth part. This delay corresponds to a frequency reduction by a two millionth part, which is a slight reddening of the light. (The figure greatly exaggerates the effect. It is not at all drawn to scale.)
While it was Einstein's earliest prediction, it proved to be the hardest to verify. The difficulty is that the sun is a very complicated object. It has many elements in it, all emitting their own frequencies, and the matter moves so that the emitted light also suffers Doppler shifts. Einstein supported early efforts to find the red shift in sunlight through the erection of a solar observatory in Potsdam, near Berlin. The Einsteinturm ("Einstein tower") was constructed in 1919-1921 and went into operation in 1924. However it never produced an unequivocal confirmation of Einstein's prediction.

Einsteinturm https://en.wikipedia.org/wiki/File:Einsteinturm_7443.jpg
A more promising source of light for testing Einstein's prediction are stars that are very much more massive than our sun. Because of their greater mass, the reddening will be greater and should be easier to detect. Light from such stars was scrutinized over the course of the twentieth century and, slowly and painstakingly, Einstein's prediction was confirmed.
A more direct test of Einstein's prediction was carried out by Robert Pound and Glen Rebka in 1960. They measured the frequency shift in gamma rays propagating downward from the top to the bottom of a tower at Harvard University. Since the rays are propagating into a region of stronger gravity, Einstein's prediction is that they will be slightly blue shifted. The amount of the shift predicted is very much less than the shift predicted for sunlight, for the gamma rays of the Pound and Rebka experiment only fall 74 feet above the surface of the earth. However with suitable refinements, Pound and Rebka were able to confirm Einstein's prediction to within one percent.
Copyright John D. Norton. February 2001;
January 2, 2007, February 15, August 23, October 16, 27, 2008; February
5, July 20, 2010, February 25, 2013. December 29, 2015. February 22,
2017. Links added November
18, 2019. April 19, October 5, 2020. Appendix added May 30, 2021.
February 4, 2022. February 25, 2024