| HPS 0628 | Paradox | |
Back to doc list
Infinite Sets
John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
http://www.pitt.edu/~jdnorton
Linked Document: Sets,
Formally Speaking
The paradoxes of the infinitely large pose a
foundational problem: can we really accept their results. Is
there not something wrong with an infinite hotel that can always
make room for more guests? Should we not draw the line at infinities of
bodies whose interactions in ordinary collision mechanics lead to
violations of the laws of conservation of energy and momentum? Perhaps
there is a contradiction lurking in the paradoxes. That view was long
held. The more recent view, as we shall now see, is just to accept that
they are counter-intuitive, but not inherently contradictory; and they
point to a new way to think about infinities.
The oldest response to these paradoxes was to take a severe option that can be traced back as far as Aristotle. According to it there is something wrong with the very idea of a completed infinity. The notion should be excised from our analyses.
Since something in the neighborhood of infinity seems useful in our thinking, Aristotle distinguished two senses of infinity: the potential and the actual. We have seen earlier how Aristotle employed the distinction in his response to Zeno's paradoxes of the dichotomy and the Achilles.
A potential infinity is characterized by its incompleteness. It manifests in systems in which an extension is always possible. Consider, for example, a sphere in ordinary space:
We can always make it bigger:
and then
and then
and even:
Potentially, a sphere can always be made larger. There is no largest sphere. The idea of an actually infinite sphere is literally nonsense. That is, it is a term "infinite sphere" that refers to nothing. For the surface of infinite sphere would have to consists of points infinitely far away from its center. But there are no such point "at infinity." Every sphere in a Euclidean space is some finite distance from a center point. The infinity is merely a potential infinity: there is no largest radius. For any radius we pick, say 10, 100, 1000, ..., there is always a larger one, 11, 101, 1001, ... Infinity is not a place picked out by the nonsensical notion of "infinite radius," where we somehow imagine that very, very distant points live.
This last example shows that an aversion to actual infinities is not always mistaken. To insist that there are infinite spheres in a Euclidean space directly contracts the property of a Euclidean space that every point in it is some finite distance from any nominated starting point. The appropriate attitude is selective. Sometimes we should limit ourselves to potential infinities. Sometimes we should not. The troublesome view is on that issues a blanket prohibition on actual infinities.
There is a striking example of a most effective and useful branch of mathematics that employed only potential infinities. This is the geometry codified by Euclid in the 4th century BC. His Elements of Geometry was the definitive treatise in geometry for millennia. It provided Newton with the mathematics he needed to formulate his celebrated system of the world.
Here is the title page of the first English edition (1582) of Euclid's Elements, translated from the Greek:

The foundation of Euclid's geometry lay in his five postulates. They asserted what exists in the world of geometry. The rest of geometry is to be constructed from what these five postulates say exists. Here is how the first two postulates appeared in this first English edition. (This early edition does not use the not standard term of "postulate.")

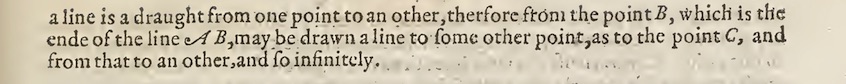
These postulates contain a similar concession to possible infinity, as opposed to an actual infinity. The first postulate says from a later translation:
1. Let the following be postulated: to draw a straight line from any point to any point.
Then the second postulate says:
2. To produce a finite straight line continuously in a straight line.
What is key here is what is not said. We would now want to say "There are infinitely long straight lines." Euclid instead just says that we can take any interval, finite in length, and produce it. Here I assume that "produce" means just "add any finite length to." If that is so, the extension can be continued indefinitely. However, no matter how many finite extensions we apply, since there are only finitely many of them, we do not arrive at a completed infinity, which would be the infinite straight line.
Perhaps Euclid limited his treatise to potential infinities through a concern for the trouble that actual infinities might cause. Or perhaps he just did not need actual infinities. In any case, the restriction did not harm the position of Euclid's Elements as the definitive treatise in geometry for thousands of years after him.
We can follow the Aristotelian spirit and apply the same thinking to sets of numbers. There are many possible finite collections of numbers. We might have
1
or
1, 3, 5, 7
or
10, 27, 56, 101
These collections manifest a potential infinity. We can keep writing down new collections. No matter how many we write down, we can always add more. Each of these collections is extendable. We can always add more numbers to them; and then more again. This notion of potential infinity is, we are to suppose, sufficient to handle responsibly all the problems that arise concerning infinities.
Where a potential infinity is always incomplete, an actual infinity is complete. The totality of all the numbers is an actual infinity. They are all there. There is no new number that can be added to them.
1,
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ...
All the paradoxes of the infinitely large depend on entities with completed infinities. If they are prohibited, then the paradoxes are gone. While this prohibition solves the problem, the general principle in solving paradoxes is to do the least harm: do not prohibit any more than really needs to be prohibited. This prohibition against actual infinities has been judged to go too far in the mainstream of mathematical thought, as we shall now see.
While this is a majority
view in mathematics, there is still a minority finitist
tradition that avoids actual infinities. We saw an example of its
thinking in the question of the truth
of propositions in arithmetic and its relation to supertasks.
There is a less severe way of responding to the paradoxes of the infinitely large. There are, we shall see, two ways in which we compare the sizes of sets. Each by itself is unproblematic. However if we apply both to the same situation they can give different results. If we do this without realizing that we are using two different ways for comparing, we end up with conflicts that appear paradoxical. Once we realize that incautious application of both ways can lead to confusion, it becomes easier to see how we can treat infinities without immediately immersing ourselves in paradoxes.
If we have two sets such that one is properly included in the other, that is, one is a proper subset of the other, then the first is smaller. The "proper" means that every element of the first set is in the second but the second has some elements not in the first.
(For more on the proper way to talk about sets, see Sets, Formally Speaking.)
if we picture sets as areas, proper inclusion arises when the smaller set occupies a smaller area in the figure than the larger set.
Under this criterion, the set of even numbers is smaller than the set of numbers:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ...
This sense of comparison is familiar and extends to antiquity. Euclid began his Elements by listing "axioms." These are propositions whose truth is so obvious that no there is no room for challenge. They are self-evident truths. They are the solid starting point of 12 books on geometry. They include such straightforward observations as:
Axiom 1. "Things which are equal to the same thing are equal to one another."
Then we have:
Axiom 9. "The whole is greater than its part, and equal to the sum of all its parts."
Here how this axiom appeared in the first English edition (1582) of Euclid's Elements:


Inclusion as a way of determining the sizes of sets is limited in its application since it requires that suitable subset relations hold before the considerations of inclusion can apply.
For example, it is easy to see that the singleton set {1} is smaller than the set {1, 2}, since {1} is a proper subset of {1, 2}. We would like to say, however, that {1, 3} and (2, 4} have the same size. However, since neither is a subset of the other, considerations of inclusion fall silent. The problem remains when we deal with infinite sets. We would like to say that the set of odd numbers:
{1, 3, 5, 7, ...}
is the same size as the set of even numbers:
{2, 4, 6, 8, ...}
However, we cannot since there are no suitable subset relations holding between them.
The following definitions allow us to proceed with slightly greater precision and avoid the problems just noted. Both conditions can only be applied in cases in which the two sets stand in suitable subset relations.
A set A is no larger than a set B under the criterion of inclusion, just if A is a subset of B.
The awkward "no larger than" condition allows the definition to be formulated in terms of subsets, as opposed to proper subsets. That leaves open the possibility that A and B are same size. Leaving this possibility open enables us to give a definition of what it is for two sets to have the same size.
Sets A and B have the same size under the criterion of inclusion, just if A is no larger than B and B is no larger than A
To see how this works, take the most general case of two sets A and B, such that A and B have a non-empty intersection. In a diagram, they appear as:
The condition for sameness of size has two parts. The first requires that A is no larger than B; that is A is a subset of B. That means that the part of A that does not intersect with B is empty:
The second condition requires that the B is no larger than A; that is, that B is a subset of A. That means that the part of B that does not intersection with A is empty.
After these restrictions, it follows that sets A and B are the same set and thus have the same size.
Finally, there is a natural extension of the first definition:
A set A is smaller than a set B under the criterion of inclusion, just if A is a proper subset of B.
These seem such natural ways of comparing the sizes of sets that, at first, it seems hard to imagine that there might be anything to conflict with them.
A second way of comparing the sizes of sets is equally familiar. Most of us do not know how many socks we have. However we are fairly sure that we have as many left socks as right socks. Or that is true at least for those of us who neatly store their stocks rolled together as a matched pair of left and right socks. (As a useful fiction, I am imagining that we mark each pair of socks as left and right.)
The criterion used is that the two sets of socks--left and right--are the same size just if we can map them one-to-one to each other. They are equinumerous.
This idea of the one-to-one mapping is key to the whole analysis. We will be using it again and again. Here is the more formal treatment of it.
Under this criterion, there are as many numbers as there are even numbers; and as many numbers as there are square numbers.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... |
| ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | ... |
| ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | |
| 12=1 | 22=4 | 32=9 | 42=16 | 52=25 | 62=36 | 72=49 | 82=64 | 92=81 | ... |
In general, any infinite subset of the natural numbers is equinumerous with the natural numbers and can be mapped one-to-one to them in this way.
If we think of subsets as areas, as in the figure above, then this one-to-one mapping appears as an expansion of the smaller area such that it fills the larger area exactly:
The effect of the expansion is to induce a one-to-one mapping from points in the smaller area to points in the larger area.
This criterion of one-to-one correspondence is a robust means of comparing the sizes of sets. It can be used with finite sets and with infinite sets. When two sets are equinumerous in this sense, we say that they have the same cardinality; or that their size is given by the corresponding cardinal number. This is a key definition for what is to come:
Two sets have the same cardinality if their members can be placed in a one-to-one correspondence. They have the same cardinal number.
In the case of finite sets, this notion is just the familiar notion of the size of the set. For example, the four-membered sets {u, v, x, y} and {1, 2, 3, 4} can be placed in a one-to-one correspondence. They have the same cardinality and the cardinal number 4.
If the members of two sets cannot be placed in such a one-to-one correspondence, then one has a larger cardinality and the other a smaller cardinality.
A smaller cardinality set can be placed in one-to-one correspondence with a proper subset of a larger cardinality set, but not vice versa.
In terms of the representation of sets by areas, the smaller cardinality area can be mapped one-to-one onto a proper subset of the larger cardinality area:
However, there is no expansion of the smaller cardinality area such that it can fill the larger cardinality area fully:
The two criteria agree, as long as we are dealing with finite sets. That makes it easy to treat them as interchangeable. You can check you have the same number of left and right socks by pairing them; or you can count how many left socks you have and how many right socks you have and check if the two counts are the same. Either procedure works and should give the same result, assuming that you have finitely many socks.

They come apart when they are applied to infinite sets. This troubled Leibniz, the great 17th century thinker. He would not compromise the Euclidean axiom: "the whole is greater than the part." He considered the case of numbers and their squares. He recognized correctly that the numbers 1, 2, 3, ... are equinumerous with the square numbers 12=1, 22=4, 32=9, ... He found this equality to be absurd:
"Therefore there are as many numbers as there are square numbers, that is, the number of numbers is equal to the number of squares, the whole to the part, which is absurd."
Stern action was needed to eliminate the absurdity. He concluded that numbers do not form a proper whole, so that the equality in number of the set of numbers and set of square numbers is escaped. This escape is a version of the Aristotelian retreat from actual infinities to potential infinities.
Until the 19th century, comparisons of the sizes of sets was carried out almost exclusively by inclusion. Georg Cantor took up the investigation of the comparisons of the sizes of sets using the criterion of one-to-one correspondence. What resulted was an opening of a whole new realm of mathematics. It is so wonderful in its scope that David Hilbert called it Cantor's "paradise." (Alas, Hilbert's positive reaction was not universal. Cantor faced considerable opposition to his ideas and suffered greatly for it.)
A major result is that not all infinities are alike. Some are bigger than others; and there are always greater infinities to be had. He classified the sizes of the infinities by transfinite numbers, using the Hebrew letter "aleph":
ℵ0, ℵ1, ℵ2, ...
The set of natural numbers, {1, 2, 3, 4,...} has the cardinality of the first of Cantor's numbers, ℵ0. ("Aleph-null") This is its cardinal number, which conveys to us its size. Merely saying "infinity" in Cantor's theory is imprecise. They are many infinities. By specifying ℵ0, we specify which infinity applies.
ℵ0
All of the infinite subsets of the natural numbers have this same cardinality. They include the square numbers, the cubes, ..., prime numbers, multiples of 2, multiples of 10, and so on for many more.
These sets are often called "countably infinite" or "denumerably infinite." That just means that the sets are of a size that we can, metaphorically, count off or number their members by using the natural numbers, 1, 2, 3, ... (The terms "countable" and "denumerable" may also be applied to finite sets, since they can also have their members counted,. There does not seem to be a universal agreement on whether this application to finite sets is a proper use of the terms. This is just a question of how we choose our definitions.)
A cardinal number like ℵ0 is used in the same way as we use natural numbers to convey the size of a set that is finite in size. The cardinality of the set {1, 2, 3, 4} is 4. That is, its cardinal number is 4. We use ℵ0 in the same way as we use "4." Here is an example:
What is the size of the set {1, 2, 3, 4}? Answer:
"4"
Analogously:
What is the size of the set of natural numbers, {1, 2, 3, ...} Answer: ℵ0.
Everything in Cantor's theory applies to finite sets as well. For example, the sets {1, 2, 3, 4} and {5, 6, 7, 8} can be placed in a one-to-one correspondence. Therefore they have the same cardinality, 4:
| { | 1, | 2, | 3, | 4 | } |
| ↕ | ↕ | ↕ | ↕ | ||
| { | 5, | 6, | 7, | 8 | } |
Nothing unexpected happens, however, in the
application to finite sets. This finite set cannot be placed into a
one-to-one correspondence with any of its proper subsets, such as {5,6}.
This last set is smaller in cardinality and has the cardinal number 2.
| { | 1, | 2, | 3, | 4 | } |
| ↕ | ↕ | ↕ | ↕ | ||
| { | 5, | 6 | ? | ? | } |
New cases arise when we consider sets of numbers that are larger than the natural numbers by the criterion of inclusion, but are of the same cardinality. Here are two cases. The integers are are all the natural numbers, zero, and the negatives of the natural numbers:
{..., -3, -2, -1, 0 ,1, 2, 3, ...}
It should not be a surprise that the natural
numbers ℕ and
the integers ℤ can be put
in a one-to-one correspondence. Here's one way to do it?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... |
| ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | |
| 0 | -1 | 1 | -2 | 2 | -3 | 3 | -4 | 4 | ... |
The explicit rule that creates this one-to-one mapping is:
Even number in ℕ
→ -(even number/2) in ℤ
so 4 → -(4/2) = -2
6 → -(6/3) = -3
etc.
Odd number in ℕ
→ (odd number-1)/2 in ℤ
so 1 → (1-1)/2 = 0
3 → (3-1)/2 = 1
etc.
Here is the original paper from 1896 in which Cantor declares that sets of the size of the natural numbers are given a cardinal number called ℵ0. He uses the German spelling for "aleph," which is "alef."
 |
The shaded heading says "The smallest transfinite
cardinal number alef-null" Below, Cantor says in shaded text that he will represent aleph-null by the symbol ℵ0. He gives the definition  The set {ν} is the set of all natural numbers, since Cantor uses the Greek letter nu, ν, as a variable ranging over natural numbers. The double overbar designates the cardinal number belonging to that set. The next shaded text says that "ℵ0 is a transfinite number equal to no finite number μ." Cantor then provides an argument that ℵ0 is not a finite cardinal number. We have that ℵ0 = ℵ0 + 1 No finite cardinal number μ satisfies this equation. As we know: 3 = 2 +1 4 = 3 +1 5 = 4 + 1 ... |
The more interesting case is the set of all rational numbers ℚ. These are all the numbers that can be written as a ratio of integers, excluding division by zero. They include the obvious fractions like 1/2, -1/2, 0 and 2/3. Also included are improper fractions like 13/7 and 101/5.
At first it seems that there must be many more rational numbers than natural numbers or integers. For if we lay out the natural numbers or the integers on a number line, they have gaps between the numbers:
... ___-2___-1___0___1___2___3___...
The rational numbers, however, are dense on the number line. That is, if we pick any two rational numbers:
... ___1________2___...
then there is always another rational number between them:
... ___1___3/2___2___...
and then between those:
... ___1__5/4__3/2__7/4__2___...
and so on indefinitely. Each of the gaps between the natural numbers is filled with infinitely many rational numbers.
The rule used here to generate new rational numbers to fill in any gap is this: for any two rationals R1 and R2, their average (R1 + R2)/2 lies between them and is also a rational number.
For example, if R1
= 37/4 R2 = 65/3, then
(R1 + R2)/2 = (3x37 + 4x65)/(3x4) =371/12
This lets us prove by reductio that there can be no finite sized gaps in the set of rational numbers. For suppose for purposes of reductio there is a gap between say R1 and R2, which would mean that there are no rationals between them. Yet (R1 + R2)/2 is a rational number that lies between them.
We might try to picture this density if we represent rational numbers by circles on the number line. There is a big gap between 1 and 2. Then a smaller gap between 1 and 1.5 and between 1.5 and 2. Each gap is filled by more rational numbers, so that none remain:
Thus, the rational numbers seem to be so numerous that they escape one-to-one correspondence with the natural numbers. Or at least that is a plausible first guess.
Cantor showed otherwise. It turns out that there is a simple scheme that allows us to place the natural numbers in a one-to-one correspondence with the natural numbers. The trick is easiest to see if we start with the positive rationals only. We lay them out in an infinite two-dimensional grid. We can then trace through the entire grid by following the diagonal paths shown. We tag each rational number as we pass it with a natural number. it follows that the positive rationals have the same cardinality as the natural numbers, Cantor's, ℵ0.
The natural scheme shown has duplications. 1/1, 2/2, 3/3, ... are all the same rational number 1. We could just ignore the duplications, for then the one-to-one mapping would be between a proper subset of the natural numbers and the rational numbers. That is enough to establish that the natural numbers and the positive rational numbers are equinumerous. A slightly more elegant approach is shown in the figure. When we come to a duplicated rational number, we just jump over it and do not tag it.
This procedure sets up the one-to-one mapping between the natural numbers ℕ and the positive rationals. It is then a simple exercise to extend this one-to-one mapping to the full set of rationals ℚ that includes zero and all the negative rationals.
This method is the standard
method used to display a one-to-one correspondence of the natural numbers
and the positive rational numbers. A much faster way
to get the same result is to write each positive rational number as m/n.
Each is then mapped to 2m3n. We know from the unique
factorization of composite numbers in arithmetic, that each m/n is thereby
mapped to a unique natural number. A one-to-one correspondence is thereby
displayed between the natural numbers and a subset of the natural numbers.
1/1 → 2131 = 6
1/2 → 2132 = 18
2/1 → 2231 = 12
etc.
It is surprising that the set of rational numbers turns out to be equinumerous with the set of natural numbers. We might well wonder about another set of numbers that is also dense on the real line. These are the real numbers, ℝ. Rational numbers can be expressed as terminating decimals
1/8 = 0.125
or as repeating decimals
1/7 = 0.142857 142857 142857 142857 ...
If we now add into the set all the numbers (positive and negative) with non-repeating decimal expansions, that is, the irrational numbers, we have the set of real numbers:
√2 = 1.4142135623730950488…
π
= 3.14159265358979323846264338327950288419716939937510...
The real numbers are also dense on the real line. Between any two real numbers there is always another one; and so on indefinitely.
The demonstration uses a rule similar to the one used with rational numbers. For any two real numbers R1 and R2, their average (R1 + R2)/2 lies between them and is also a real number. Since the rational numbers are already dense on the number line, we need further argumentation to show that the irrational numbers added are also dense on the number line. The averaging argument does not show it. We can take two irrational numbers and find that their average is a natural number. Consider (10+π) and (10-π). They are both irrational numbers, but their average is 10. To see that the irrational numbers are dense on the number line, take any two, different rational numbers, r1 and r2, it is easy to see that there are infinitely many in irrational numbers between them. For example, consider 1.1 and 1.2. The irrational 1.1235687389578... (assumed non-repeating) is one of infinitely many irrational numbers lying between them.
It turns out, however, that the real numbers are more numerous in cardinality than the set of natural numbers. That they are more numerous is shown by one of the most celebrated arguments in Cantor's set theory, "diagonalization." Cantor's argument is a reductio argument. He assumes for purposes of reductio that there is a one-to-one mapping between the natural numbers and a subset of the real numbers lying in the interval (0,1). (If he can show that this subset of real numbers is already too big to be put in one-to-one correspondence with the natural numbers, then the same must true of the bigger set of all real numbers.)
Let us assume that we have found such a one-to-one correspondence. It might look like this:
1 ↔
0 . 1 4 1 5 9 2 6 ...
2 ↔ 0 . 5 3 5 8 9 7 9 ...
3 ↔ 0 . 3 2 3 8 4 6 2 ...
4 ↔ 0 . 6 4 3 3 8 3 2 ...
5 ↔ 0 . 7 9 5 0 2 8 8 ...
6 ↔ 0 . 4 1 9 7 1 6 9 ...
7 ↔ 0 . 3 9 9 3 7 5 1 ...
...
We consider the digits along the shaded diagonal. These digits form another real number:
0 . 1 3 3 3 2 6 1 ...
All we need now to complete the reductio is to find any real number that differs from this one in every digit. We might replace a 1 by 2, a 2 by a 3, ..., a 9 by a 0. then we have
0 . 2 4 4 4 3 7 2 ...
This new number cannot appear anywhere in the one-to-one correspondence assumed:
It cannot correspond to
1, since it differs from real corresponding to 1 in the first digit.
It cannot correspond to 2, since it differs from real corresponding to 2
in the second digit.
It cannot correspond to 3, since it differs from real corresponding to 3
in the third digit.
and so on for all the digits.
That is, we have shown that this assignment of real numbers to natural numbers is not one-to-one. The real number we have constructed is missing from the correspondence. There is nothing special about the particular correspondence suggested. No matter which correspondence we might propose, the diagonalization construction will always produce a real number that eludes it.
The reductio is complete. The assumption that we can have a one-to-one correspondence between the natural numbers and real numbers produces a contradiction. The real numbers form an infinite set larger than the infinite set of the natural numbers. It is natural to assume that this larger set carries Cantor's next cardinal number ℵ1. However deciding just which sets ought to carry this next cardinal number proves to be a messy matter and will be discussed below under the heading of the "continuum hypothesis."
Since the real numbers form a continuum, such as the continuum of a line in geometry, it is often called "continuum- sized." In contrast, sets of the size of the natural numbers or smaller are called "countable," since we can enumerate their elements with ordinary counting numbers 1, 2, 3, ... Sets of the size of the real numbers, however, would require something as big as the real numbers if an enumeration is to succeed.
The method of diagonalization is one that will return many times. It is an important mode of proof when we explore infinite systems. Its core idea is to turn something against itself and thereby to establish a contradiction.
Here is the short paper in which Cantor announces, with obvious satisfaction, that he has discovered a proof of great simplicity ("grosse Einfachheit") that shows that some sets are larger in cardinality than others.
 |
In the shaded text, Cantor sets up a very simple case
of a set M whose elements consist of an infinite sequence
of symbols, either m or f. While he does not say it, we can guess that m or f come from the German mannlich/weiblich = masculine/feminine. He then imagines that all possible of these sequences can put into a list, indexed by the natural numbers 1, 2, 3, ... 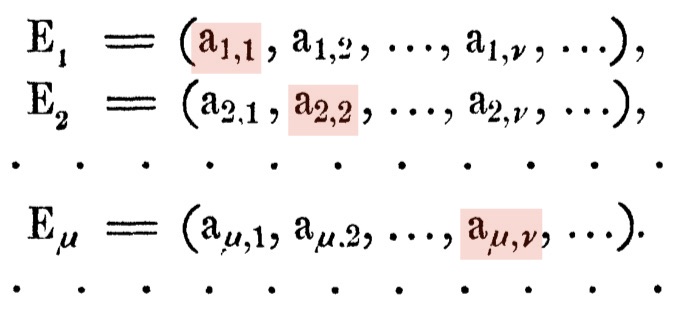 He next constructs a sequence E0 that is not in the list. He does this by defining a sequence of symbols b1, b2, b3, ... that form E0 and demonstrating that it will always be different from the shaded diagonal elements of the list, shown above. He writes: "Therefore if aν,ν = m, then bν = w, and if aν,ν = w, then bν = m." The proof is completed when he notes that E0 can appear nowhere in the list since, for all values of μ, the equation bμ = aμ,μ is excluded ("ausgeschlossen"). Cantor is obviously pleased with the proof. He extols its great simplicity and, on the next page, notes that it can be generalized to show that there is no maximum cardinal number. (We shall return to this powerful result as "Cantor's theorem.") |
There are many distinct sets equinumerous with the real numbers. Here are just a few of them.
Consider the closed interval of real numbers [0,1] and [0,2]. That is, all the real numbers lying between 0 and 1, including 0 and 1; and all the real numbers lying between 0 and 2, including 0 and 2. They are equinumerous and of continuum size.
The simple proof is to note that each real number r in [0,1] stands in a one-to-one correspondence with each real number 2r in [0,2]. That is, to find out what real number is assigned to any real number, r, just double it:
0 → 0, 1 → 2, 2 → 4, 1/7 → 2/7, 1/√2 → 2/√2, 1/π → 2/π, ...
r → 2r
A geometric figure illustrates the one-to-one correspondence:
There are many more examples. Another example concerns the open set of real numbers (0,1), that is, all real numbers between 0 and 1, not including 0 and 1. It can be placed in a one-to-one correspondence with (0,∞), that is all real numbers greater than 0. The correspondence can be brought about in many ways. A simple algebraic rule suffices:
r in (0,1) is mapped to r/(1-r) in the positive reals.
r → r/(1-r)
That is,
r=0.01 is mapped to 0.01/(1-0.01) = 0.01/0.99 = .010101....
r = 0.5 is mapped to 0.5/(1 - 0.5) = 1
r= 0.99 is mapped to 0.99/(1-0.99) = 0.99/0.01 = 99
The geometrical representation lays out the values of r on the right hand, vertical side of the unit square shown in the figure below. A ray from the top left hand corner maps the various values of r to their corresponding values of r/(1/r) on an indefinitely extended horizontal line, aligned with the base of the square:
That this figure represents
the mapping r → r/(1-r) follows from a consideration of similar
triangles. The figure below redraws a portion of the above
geometrical representation. The triangles ABC and CDE are similar. Hence
the ratio of the first triangle's sides, AB:BC equals the corresponding
ratio of the second triangle's sides, DE:CD. That is
AB:BC = 1/(1-r) = DE:CD = [ r/(1-r) ]/r = 1/(1-r)
A more traditional way to display the correspondence is with the geometric figure below. It shows how to map a unit interval on the quarter circle to the infinite line of all positive real numbers.
These mappings are richer than what is needed to establish mere one-to-one correspondence. They also preserve the order the two sets of numbers mapped. Here order means that "less than" relations are preserved in the mapping. That means that that a richer equivalence is actually being demonstrated. It is not just cardinal equivalence, but what is called "ordinal" (or order preserving) equivalence. This richer concept is not explored here.
The mapping between finite and infinite intervals of real numbers has a rich history. An early form of it is found in Arnaud and Nicole's La Logique ou l'art de penser [Logic or the Art of Thinking], also known as the "Port Royal Logic." It was a definite treatise on logic and scientific method in the 17th century.

Their map is introduced through the artifice of a ship that leaves port to sail away on an infinitely extended, flat sea. The position of the ship's bottom is viewed from shore. As the ship departs, its position rises in the observers field of view and the projection of it in a lens descends. (In the figure below, I have replaced the lens with a simple viewing screen.) As the ship moves away equal distances, the projection point descends toward an accumulation point. Each step takes less space, shrinking without limit. The infinitely extended sea is mapped onto a finite screen.
Sailboat image from Sailboat image from T. R
Biddel, A Treatise on the Construction, Rigging, & Handling of Model
Yachts, Ships and Steamers. London: Norrie & Wilson, 1883. p. 35.
Arnaud and Nicole's goal, however, was not to
demonstrate the one-to-one correspondence of the points of the infinite
sea and the points of the finite screen. That was only shown as an
incidental result subordinate to their real goal. They wanted to argue
for the infinite divisibility of space. They took as an
acceptable premise that a flat sea could in principle always be extended
by some fixed distance. The projection points of the newly acquired
positions at sea would then correspond to ever smaller displacements on
the viewing screen. Since these displacements could become arbitrarily
small, the construction shows the infinite divisibility of space.
Their text reads:
"Certainly, while we might doubt whether extension can be infinitely divided, at least we cannot doubt that it can be increased to infinity, and that we can join to a surface of a hundred thousand leagues another surface of a hundred thousand leagues, and so on to infinity.[footnote: Descartes, Principles of Philosophy, Pt. II, art. 21, Philosophical Writings, vol. I, p. 232.] Now this infinite increase in extension proves its infinite divisibility. To understand this we only have to imagine a flat sea that is increased infinitely in extent, and a vessel at the shore that leaves the port in a straight line. It is certain that when the bottom of this vessel is viewed from the port through a lens or some other diaphanous body, the ray that ends at the bottom of this vessel will pass through a certain point of the lens, and the horizontal ray will pass through another point of the lens higher than the first. Now as the vessel goes further away, the point of intersection with the lens of the ray ending at the bottom of the vessel will continue to rise, and will divide space infinitely between these two points. The further away the vessel goes, the more slowly it will rise, without ever ceasing to rise. Nor can it reach the point of the horizontal ray, because these two lines that intersect at the eye will never be parallel nor the same line. Thus this example provides at the same time proofs of the infinite divisibility of extension and of an infinite decrease in motion."
At first, it seemed that all infinite sets are the same size. The natural numbers are the same size in cardinality as the integers, which is the same size in cardinality as the rational numbers. Just when it seems that every infinite set might be the same size, it turned out the real numbers form a set that is larger in cardinality that the natural numbers.
Have we now found in the real numbers the biggest set? Are there sets still bigger in cardinality than the real numbers? If not the reals, might there be a biggest set larger than it? It would seem a simple matter to form such a set. Just to collect together all the sets and form their union. Call it the universal set. It has the property that every set would be a subset of this universal set.
Simple as this idea sounds, it turns out that there can be no set that is biggest in cardinality. For any set we are given, we can always find one that is larger than it in cardinality. This curious circumstance is the starting point of foundational work in set theory that came to dominate the 20th century. We shall see more of it in a chapter to come.
Cantor found a simple means of ascending to higher infinities. It will enable us to see that there is no biggest set.
The means is through the notion of a power set.
Consider some set, say S = {a, b, c}. Its power set is the set of
all its subsets
P(S) = {{a},
{b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}, {}}.
This set S has 3 elements. The power set has 23
= 8 elements. We arrive quickly at this formula once we realize
that we can identify each subset of S by answering 3 questions:
Is the first element a in the set? (yes/no)
Is the second element b in the set? (yes/no)
Is the third element c in the set? (yes/no)
Each question can be answered in two ways (yes/no). Since there are 3 questions, the total number of answers is:
2 x 2 x 2 = 23 = 8.
The set:
The power set:
The general result is that a set with n elements has a power set with 2n subsets. We can identify each element of the power set by answering n of these yes/no questions.
The jump from n to 2n is a big jump. If we now make the jump in the case of infinite sets, we are jumping from one cardinal number to a bigger one.
We can see that this happened in the transition from the natural numbers to real numbers in the following way. Each subset of natural numbers in the power set of the natural numbers can be identified by answering infinitely many questions of the form:
Is 1 in the set? (yes/no)
Is 2 in the set? (yes/no)
Is 3 in the set? (yes/no)
...
What results is an infinite string of yes-no-no-yes-yes-yes-no-yes-... with each string identifying a unique subset of the natural numbers. If we copy the way that we treated the power set of a three-membered set above, we can represent the size of the power set of the natural numbers by multiplying a countable infinite of 2's together:
2 x 2 x 2 x 2 x 2 x ... = 2ℵ0
The resulting formula, "2ℵ0," is "two to the power of aleph-null." It is the cardinal number that represents the size of the power set of the natural numbers.
We can take this infinite string of yes-no answers and replace each yes by a 1 and each no by a 0. We can use the resulting string of 1's and 0's to form a real number such as:
0 . 1 0 0 1 1 1 0 1 0 ...
If we read this as a base-2 binary number, it is a real number between 0 and 1. All the possible encodings of the answers exhaust the real numbers between 0 and 1. The overall effect is that we have shown that all the subsets of the natural numbers can be mapped one-to-one to the real numbers between 0 and 1. This set, we saw above, is larger than the set of natural numbers and is of continuum size. That is, the cardinality of the set of real numbers is
2ℵ0
We have seen examples above of how taking a power set carries us to a set of higher cardinality. Cantor's theorem tells us that this is a quite general result. Take the power set of some set and always end up with a set of higher cardinality:
Cantor's Theorem: The power set of any set is strictly larger than the set and cannot be placed in a one-to-one correspondence with the set.
This assertion is of foundational importance in investigations of infinity. It tells us that we can always find a larger infinity by taking the power set of the set presently under consideration. What results is an infinity of infinities, each larger in cardinality than the one before. If the infinite set is S, then the ascent arises as:
S → P(S) → P(P(S)) → P(P(P(S))) → P(P(P(P(S)))) → ...
The theorem turns out to be rather simple to prove. The proof is another diagonalization. We proceed with an assumption for reductio. Let us say that we have found a one-to-one correspondence "f" between some set S = {a, b, c, ...} and its power set P(S) = { {}, {a}, {a b}, ...} There is no presumption on the size of S. It can be infinite of any order. The one-to-one correspondence might look something like this:
a ↔ f(a) = {a, b, c}
b ↔ f(b) = {a, c, d, e, ...}
c ↔ f(c) = {e, f, g, ...}
and so on for all elements of S.
We now form the diagonal set Diag by the following rule:
a is an element of Diag, exactly in case it is not
an element f(a).
b is an element of Diag, exactly in case it is not an element f(b).
and so on for all elements of S.
f(a) = {a, b, c}
so a is NOT in Diag
f(b) = {a, c, d, e, ...}
so b IS in Diag
f(c) = {e, f, g, ...}
so c IS in diag
and so on.
We end up with Diag = {b, c, ...}
With this diagonal set defined, we quickly arrive at a contradiction. The set Diag is a subset of S and thus should be an element of the power set P(S). Therefore it should appear somewhere in the one-to-one correspondence. Yet by its construction it cannot be the set to which any element of S is mapped.
It cannot be f(a), since
by construction Diag has a as an element exactly if f(a) does not.
It cannot be f(b), since by construction Diag has b as an element exactly
if f(b) does not.
and so on for all the remaining elements of S.
The reductio is complete. The assumption made for reductio is refuted. The elements of any set S cannot be mapped one-to-one onto its power set P(S). The power set is an order of infinity larger.
Cantor's transfinite arithmetic supposes the existence of cardinal numbers of ever increasing size. We might write them as a sequence:
ℵ0, ℵ1, ℵ2, ...
There will be no largest cardinal number. For any set, Cantor's theorem assures us that there is always a larger set, its power set, and that larger set will have a larger cardinal number.
It would be natural to assume that the cardinal number of the set of real numbers, 2ℵ0, is the the next highest cardinal number after the cardinal numbers of the set of natural numbers, ℵ0. It seems quite plausible that this is so. This plausible supposition has a name, "the continuum hypothesis." It asserts that the next highest cardinal number after the ℵ0 of the natural numbers is the cardinal number of the continuum, 2ℵ0. We can write the hypothesis symbolically as:
ℵ1 = 2ℵ0 (??)
The hypothesis would be false if it turned out that the cardinal number 2ℵ0 is actually equal to a larger cardinal number such as ℵ2 or even ℵ3. It seems a simple matter to check the hypothesis. We would look for a set larger than the set of natural numbers but smaller than the set of real numbers, where that set is larger in cardinality than the natural numbers and smaller in cardinality than the set of real numbers. This check is simple enough to state and the outcome known. No one has been able to find a set of intermediate cardinality.
That, alas, does not decide the matter. That no one can find such a set does not mean that such a set does not exist. Perhaps we just have not been diligent enough in our search. Or, more plausibly, we finite humans have limited methods of constructing sets through manipulation of finitely many symbols. Once we are in the world of infinite sets, might the set we seek simply be something that outstrips our meager powers of description?
The worst case for us would be that the truth of the continuum hypothesis just is something outside our demonstrative powers. It might be true; or it might be false. But our demonstrative powers are unable to decide. This worst case is the one we have. We can describe this worst case is more precise terms as follows. Take our best theory of sets and add either the continuum hypothesis or its negation to its axioms. Either case proves to be consistent. That is, we can tell a consistent story of infinite sets in which the continuum hypothesis is true; and we can tell a consistent story of infinite sets in which it is false.
How we should think about this curious outcome goes well beyond what can be treated here. Perhaps we can say this much. If we think that infinite sets exist independently of our theories, then we have learned that our theories are too weak to grasp them fully. If we think that infinite sets are conjured into being by our theories, then once again those theories are unable to find a principled reason to choose a system in which the continuum hypothesis is true as opposed to one in which it is false. We can just choose which we want.
This curious supertask combines issues to do with supertasks with issues to do with infinite sets. We are to imagine a countable infinity of balls numbered 1, 2, 3, ... and an urn of limitless capacity. In the span of time from one minute to midnight ( time "-1") to midnight (time "0") we undertake the following supertask:
At time -1, we place balls 1 to 10 in the urn and
remove ball 1.
At time -1/2, we place balls 11 to 20 in the urn and remove ball 2.
At time -1/3, we place balls 21 to 30 in the urn and remove ball 3.
At time -1/4, we place balls 31 to 40 in the urn and remove ball 4.
and so on until time 0.
Here is the first stage initiated at time -1 of the supertask. It starts with:
Then balls numbered 1 to 10 are moved to the urn:
Then ball number 1 is removed:
The supertask continues similarly with the next ten balls. Stage 2, initiated at time -1/2, begins with
Balls numbered 11 to 20 are moved into the urn:
Then ball number 2 is removed:
The supertask continues through the remaining stages 3, 4, 5 and so on infinitely.
The question is: How many balls are in the urn at midnight?
There is an almost irresistible answer: At each stage, we put 10 balls into the urn and removed one. So at each stage the urn gains a net of 9 balls. There are infinitely many stages at times -1, -1/2, -1/3, ... so the urn must have infinitely many balls in it at midnight.
Tempting as this answer is, it turns out to be wrong. What reveals the error is another question: Which balls are in the urn at midnight? Each ball has a number, so if there is a ball in the urn we must be able to identify its number. We quickly see that there are none:
At time -1, ball 1 was removed.
At time -1/2, ball 2 was removed.
At time -1/3, ball 3 was removed.
At time -1/4, ball 4 was removed.
and so on for all balls.
Thus, at midnight, there can be no numbered ball in the urn. Since every ball has a number, it follows that there can be no balls in the urn.
A tabular representation helps make the situation clearer:
| Time | Balls in urn | Count of balls in urn | Balls removed |
| -1 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 | 1x9 = 9 | 1 |
| -1/2 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 16, 17, 18, 19, 20 | 2x9 = 18 | 1, 2 |
| -1/3 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 | 3x9 = 27 | 1, 2, 3 |
| ... | ... | ... | ... |
| 0 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ... | 0 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ... |
As the supertask progresses, we see that the set of balls in the urn is eaten away, one by one, starting at the smallest number and working up through the entirety of the numbers. At any finite stage prior to midnight, however, the urn will contain a large number of balls. As midnight approaches, the number of balls in the urn will exceed any fixed number we care to name.
More than 100? At stage -1/100, there are 9x10 =
900 balls in the urn.
More than 1,000? At state -1/1,000, there are 9x1,000 = 9,000 balls in the
urn.
and so on for any number we can name.
But then, at midnight, they are all gone!
What this supertask illustrates is an oddity of infinite cardinal arithmetic. We are used to simple subtractions in arithmetic:
10 - 10 = 0
100 - 100 = 0
However if we are subtracting an infinity from an infinity, the result is underspecified:
∞ - ∞ = anything all
If the infinity is the set of natural numbers, we can take away the infinite set of even numbers and be left with an infinity, the odd numbers:
∞ (all numbers) - ∞ (even
numbers)
= ∞ (odd numbers)
Or we might just subtract all numbers greater than 10 and be left with a finite set of just ten numbers:
∞ (all numbers) - ∞ (numbers greater than 10) = 10
Finally, we might subtract all numbers and end up with zero:
∞ (all numbers) - ∞ (all
numbers) = 0
The particular schedule specified in the urn supertask determines which of these or many other subtractions are implemented. The schedule in the supertask above implements this last subtraction. In a later chapter, the urn supertask is investigated further. There we will see how other schedules of removals lead to different numbers of balls remaining in the urn at the conclusion of the supertask.
Can you show that all natural numbers {1, 2, 3, 4, 5, ...} can be placed in one-to-one correspondence with the set of all integers {... -2, -1, 0, 1, 2, 3, ...}?
Can you show that all positive rational numbers, {1, 1/2, 2, 1/3, 2/3, ...} can be placed in one-to-one correspondence with the set of all positive and negative rational numbers, {1, 1/2, 2, 1/3, 2/3, ... -1, -1/2, -2, -1/3, -2/3, ...}?
Can you show that the set of all pairs of natural numbers {<1,1>, <1,2>, <1,3>, ..., <2,1>, <2,2>, ...} can be placed in one-to-one correspondence with the natural numbers?
Can you show that the set of all finite
subsets of natural numbers can be placed in one-to-one correspondence with
the natural numbers?
(Hint: The prime numbers are 2, 3, 5, 7, ... and each composite number can
be written uniquely as a product of prime numbers. e.g. 5,445,468 = 22
x 34 x 75.)
Can you show that the set of infinite
subsets of the natural numbers can be placed in one-to-one correspondence
with the natural numbers?
(Hint: diagonalization?)
Can you find variants of the Ross-Littlewood Urn Supertask that leaves the urn at the end of the supertask filled with infinitely many balls; or just filled with 10 balls.
June 24, September 18, 27, October 6, December 7, 2021. December 21, 2022. February 18, 2023.
Copyright, John D. Norton