Incommensurability

John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
http://www.pitt.edu/~jdnorton

Paradoxes of impossibility arise when we have some task that appears to be quite achievable. However, try as we might, we can find no way to do it. And then with further analysis it turns out that the task set is provably impossible. We shall explore the earliest of these here, the ancient scandal of the incommensurability of the sides of an isosceles, right angle triangle. In a subsequent chapter, we will look at paradoxes of impossibility concerning classical geometric constructions and computation.

As a warm up before we look at the historically important examples, we shall look at a few recreational puzzles in which the basic elements of impossible tasks already appear. We are given a simple challenge that looks easy enough to accomplish. No matter how hard we try, however, we fail. We then find that the task is provably impossible.

The Three-Coin Game

We are allowed to flip any two of them; and flip any two of them again, as often as we like. For example we may flip the first two

We can keep going, flipping pairs of coins as long as we like. The goal is to end up with three coins showing tails:

Try it, if you like, to get a sense of the inevitability of failure.

It does not take too long to realize that the task is impossible. Attempts at solution seem quickly to run out of moves. While we may suspect strongly that the task is impossible, can we prove it?

The proof turns out to be quite easy. It all depends on a "parity" count. That is we assign a score to each arrangement of coins that equals how many heads are showing:

Call 1 and 3 "odd" parity; and 0 and 2 "even" parity. The controlling fact is that flipping two coins cannot change the parity of the set of coins. There are two cases:

• If the two coins have opposite faces showing, then the number of heads is unchanged.

• If the two coins have the same faces showing, then the number of heads is increased or decreased by 2.

If we start with three heads showing, we have a head count of 3 and thus odd parity. Nothing we do can escape configurations with odd parity. Flipping two coins either leaves the head count unchanged or alters it by 2. All accessible configurations, then, have a head count of 3 or 1 and are odd parity.

The reverse situation applies if we started with three tails. Then we could not transform the set to three heads.

Overall, there are eight combinations possible. Four of them are mutually accessible with pairs of flips; and the other four are mutually accessible with pairs of flips. But parity counts preclude us moving between them.

The Fifteen Puzzle

The coin flipping game is so simple that everyone sees through it pretty quickly. An essentially similar game has proven to be much harder to see through. The fifteen puzzle was invented in the later nineteenth century. In it, fifteen blocks can slide around in a 4x4 square frame:

W. W. Rouse Ball, Mathematical Recreations and Essays. 9th ed. London: MacMillan and Co. 1920. p. 225. Rouse Ball's discussion of the problem is here.

Here is a depiction of it from a 19th and 20th century book on mathematical recreations:

The starting configuration is shown above. The blocks can be moved around, by sliding a block into the one empty square. Many other configurations are then possible, such as the one shown below:

The goal, however, is to produce a quite particular end configuration. In it everything is as in the original configuration with the exception that the last two blocks, 14 and 15 are switched.

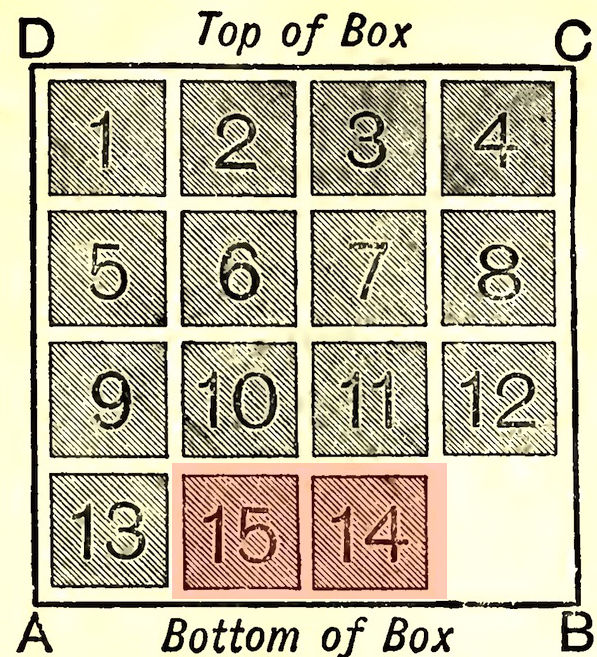
The challenge proved to have enormous appeal. The puzzle became widely popular. An account of it was given in 1879 in a mathematical journal. The account concluded:

Wm. Woolsey Johnson and William E. Story, "Notes on the "15" Puzzle,"American Journal of Mathematics, Vol. 2, No. 4 (Dec., 1879), pp. 397- 404. on p. 404.

"The "15" puzzle for the last few weeks has been prominently before the American public, and may safely be said to have engaged the attention of nine out of ten persons of both sexes and of all ages and conditions of the community."

Once again a simple parity argument turns out to be sufficient to show the difficulty. Any attempt to solve the problem requires that the single empty square migrate over the frame and be returned to its starting place in the lower right hand corner. We can represent the accessible configurations just by listing the squares in order, row by row. The starting configuration is:

New configurations arise when the order of numbers in this list changes. The simplest change involves flipping just two adjacent numbers, such as

The condition that the empty square must return to the lower right hand corner places a restriction on the accessible configurations. Only those configurations accessible through an even number of flips of adjacent numbers are possible. We may flip as many as we like, as long as we make an even number of flips. It then follows that exactly half of all configurations are accessible. This one above is accessible, for example:

However the configuration that wins the prize is not accessible since it is arrived at through one flip only:

The other half of the possible configurations are accessible from this last configuration.

For a fuller discussion of mathematics, see Rouse Ball's discussion. However we can see fairly quickly why an even number of flips are required. All moves involve the empty square moving left-right or up-down. A left-right move does not alter the order of the numbers. An up-down move, however, leads one square to jump over the three ahead or behind it in the list. For example, if we move the 12 square in the starting configuration one square down, it jumps over the squares 13, 14 and 15:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 empty

to

1 2 3 4 5 6 7 8 9 10 11 empty 13 14 15 12

This consists of three flips of adjacent numbers:
12 flips with 13, then 12 flips with 14; then 12 flips with 15.

That is, each up-down move of the empty square corresponds to an odd number of flips. The empty square must return to the bottom right hand corner, it follows that every upward move is matched by a downward move. That is, there must be an even number of up-down moves. An even number of up-down moves means that the manipulation combines an even number of sets of three flips. Overall, an even number of threes is itself an even number.

That is, any manipulation must involve an even number of flips.

The Three (Block) Puzzle

The details of this solution to the fifteen puzzle are not too hard to grasp, but they do involve many steps. A greatly simplified version of the puzzle gives us the same basic behavior and it is plainly visible. In this puzzle, there are just three blocks:

The blocks slide as before into the one empty square and that square is returned to the lower right hand corner at the end of the manipulations. It is easy to see that only three of the six possible configurations are accessible from this starting position. They are:

The Pythagoreans

One of the oldest of the paradoxes of impossibility and perhaps one of the oldest of provocations was a discovery attributed by tradition to the ancient Pythagoreans. They were a school of philosophers founded by Pythagoras of Samos in the 6th century BCE, at the inaugural moments of the Greek tradition in philosophy. The Pythagoreans were as much a school of philosophers as a cult. Their members were required to live an ascetic life governed by many rules. It is traditional to attribute to the Pythagoreans the results to be developed here. They are the Pythagorean theorem and the irrationality of the square root of two. The latter is attributed to the Pythagorean, Hippasus of Metapontum. However all these attributions are in doubt for lack of clear sources.

Nonetheless, the historical legends are engaging. Hippasus, it is said, discovered an impossibility so disturbing to the Pythagoreans that he was drowned at sea.

A numerical foundation for geometry

The Pythagoreans, by tradition, took as a fundamental principle of nature that "all is number." That principle worked well in music. Harmonious chords are produced by plucking stretched strings whose lengths stand in simple numerical ratios.

Whether the Pythagoreans actually proved the result as a theorem in some proof system seems less likely. The result really only can be properly called a theorem when such a proof is provided, such as is given in Euclid's Elements.

Similar whole number ratios initially seem able to express the facts of geometry. Here the Pythagorean theorem, as it later came to be known, is the key result. According to it:

The square of the length of the hypotenuse of a right angle triangle is equal to the sum of the squares of the lengths of the other two sides.

The celebrated application is through Pythagorean triples, such as (3, 4, 5), (5, 12, 13) and (8, 15, 17). They conform with the condition in the Pythagorean theorem since

It follows that the associated right angled triangles have sides that can be represented by whole numbers. One might imagine beads to be laid along each side. A 3-4-5 right angle triangle has sides of 3 beads, 4 beads and 5 beads.

The square root of two

What upset this promising approach was the simplest of right angle triangles. It is an isosceles, right angle triangle, in which the right angle is enclosed by two equal sides. If we take each side to be of unit length, the hypotenuse must be of length √2, the square root of 2. Pythagoras' theorem tells us:

No whole numbers can deal with this simple case. √2 lies somewhere between 1 and 2. The obvious remedy is that we need to use many more numbers on each side. We come pretty close to capturing the geometric relations if we assign ten to the smaller sides and 14 to the hypotenuse.

We press on. What about assigning 100 to the shorter sides and 141 to the hypotenuse? We are closer, but still not at the equality required by Pythagoras' theorem:

We could continue the exercise. However as you all surely know, it is fated to fail There are no whole numbers that can be assigned to the sides and the hypotenuse so that Pythagoras' theorem can be satisfied.

Irrationality, Incommensurability

This is sometimes described by the assertion that the sides and the hypotenuse are "incommensurable." That means that there is no common measure for both. Here, we would think of the beads in the figure as unit measuring sticks. We might measure a smaller side in inches and get a whole number. Then we will not get a whole number for the hypotenuse. We might instead use a smaller unit of measure, say, a millionth of an inch. We would still not find whole number lengths for all the sides.

The length of hypotenuse divided by the length of side is irrational. We now represent this fact by writing this ratio of lengths, the square root of 2, as a non-terminating, non-repeating decimal:

The ratios tried above are simply drawn from the first few digits of this decimal expansion.

By drawing more digits, we can come closer to the ratios required by the Pythagorean theorem. However no finite set of them can satisfy the theorem exactly.

This failure was a disaster for the Pythagorean program. It showed that a whole number foundation for geometry could not be found.

Traditionally, this failure led the Greek tradition to replace numbers as the foundation for geometry by geometrical entities. The revised approach takes points, lines, surfaces and volumes as the primitive notions that are posited as the foundation of geometry.

We can see this shift in a subtle reconception of the Pythagorean theorem. As stated above, it is a relation among numbers: the squares in the theorem are simply multiplications. "The square of the hypotenuse" refers to taking the number that measures the hypotentuse and multiplying it by itself.

The traditional Euclidean formulation of the Pythagorean theorem replaces this multiplication with a geometric construction: "the square ON the hypotenuse." and it is expressed in terms of the areas of these squares.

The square on the hypotenuse is equal [in area] to the sum of [the areas of] the squares on the other two sides.

(This is the diagram in Billingsley's 1482 first English translation of Euclid's Elements.)

Algebraic Proof
of the Irrationality of √2

The traditional demonstration of the irrationality of √2 resides is a short piece of algebra. It is a proof by reductio:

We assume moreover that we have eliminated all common factors from p and q. For example, we would not use the ratio 14/10 since the two numbers have a common factor 2 that can be cancelled: 14/10 = 7/5.

It follows that p² is an even number. This is only possible if p is itself even. (If p were odd, then p² would also be odd.) That is, there is a whole number a such that

It now follows by similar reasoning that q is also even. That is, both p and q are even and so share a common factor of 2.

Geometric Proof
of the Irrationality of √2

The algebraic proof works and works well. However it is unsatisfying in that it makes no obvious connection with triangles and geometry. That geometric connection can be made in a variation of the proof.

The basis of the algebraic proof is that we suppose we have an irreducible ratio of whole numbers for √2, p/q, that is, p and q share no common factor. We then show that both p and q are even numbers, so that, contrary to the assumption, they do share a common factor. While this completes the reductio, it also leads to the conclusion that √2 can be represented by a ratio of whole numbers smaller than p and q.

A geometric version of this proof shows how to construct a smaller right angle triangle that has this smaller-number ratio. it depends on an important fact about all right angle triangles: they are self-similar. If we take any such triangle and raise a perpendicular from the hypotenuse to the right angle, we divide the triangle into two smaller triangles. Each of them is similar to the original triangle.

That is each of them has the same corner angles and, if scaled up, would be identical with the original triangle.

The proof that all right angle triangles are self-similar is quick. The angles at vertices A and B are α and β respectively and the remaining angle is a right angle, 90^o. They must sum to 180^o. Hence we know that
α = 90^o - β and β = 90^o - α
If we use these relations to find the two angles at vertex C, it follows that they must be β and α respectively, which proves the similarity of the smaller triangles to the larger one.

This property of self-similarity is fundamental. It is sufficient to enable a quick proof of Pythagoras' theorem. If we label the sides as shown, the theorem follows from taking the ratios of corresponding sides in the three triangles. They are:
     c/b = b/y   and   c/a = a/(c-y)
If we multiply out the fractions, we recover:
     b² = cy and a² = c² - cy
Eliminating cy gives Pythagoras' theorem:
     a² + b²= c²

An isosceles, right angle triangle has a special property: the two smaller triangles are the same size and, in forming them, the hypotenuse is divided exactly in half. That is, if we divide the triangle in half as shown, we find that each half of the triangle is just a smaller copy of the bigger triangle; and that each smaller copy has the same ratio of sides of √2 to 1.

That self-similarity divides the hypotenuse exactly into half = 1/2 gives the factor of 2 that figures in the proof of the irrationality of √2. It is assumed for purposes of reductio that the hypotenuse is of length p in some unit and the other two sides are each of length q.

The two whole numbers p and q are selected such that p has the smallest value possible; that is, if there are any common factors among p and q, they are factored out. We already have from the Pythagorean theorem that p is greater than q since

If the self-similarity illustrated above is to hold, it must be possible to divide the hypotenuse exactly in half. That means that p must be an even number. We bisect the hypotenuse into two equal lengths of p/2 and connect the midpoint to the right angle.

We now have two smaller isosceles right angled triangles. Each has a hypotenuse of length q and the lengths of the other two sides are p/2. We have a contradiction with the original assumption:

We assumed hypotenuse/side
= p/q and p was the smallest whole number that can serve.
We infer that hypotenuse/side
= q/(p/2), where whole number q is less than p.

The Shrinking Construction

While this completes the proof, a striking extension of it is possible. The construction above lets us build a smaller, right angle triangle within the larger one. We can iterate. Within this smaller right angle triangle, we can construct another still smaller right angle triangle; and so on indefinitely.

Each of these indefinitely nestled, right angle triangles has equal length sides enclosing the right angle; and with each two steps in the nestling, the hypotenuse is halved. As the halving continues, we will arrive at triangles with hypotenuses of decreasing sizes .

No matter how large the length p of the largest triangle is made, we will eventually run into contradictions:

• The smallest length for p is just one unit. In that case, there is no smaller unit possible for q. The ratio p/q cannot be formed at all, contradicting our original assumption that there is some ratio for p/q.

• More generally, we might terminate the construction with p equal to an odd number: 5 or 25 or 111 or something else. Whatever that odd number may be, the hypotenuse can no longer be divided in half. Since that division is necessary for the geometric property of self-similarity, we have arrived at a contradiction with the properties of isosceles, right angle triangles.

This construction may seem to be too powerful. It depends on the similarity of a right angle triangle with a smaller version of itself. Can this same property of self-similarity enable us to prove too much? For example, a square has the properties of being self-similar with a smaller copy of itself; and that smaller copy with a still smaller copy; and so on indefinitely:

This indefinite nestling produces nothing troublesome. All we can infer for each of the squares is that the number of units measuring the vertical side equals the number measuring the horizontal side. This remains so, even if we shrink the square to one with sides equal to the smallest units we may suppose.

Can this shrinking proof be used to prove that no right angle triangles can have sides of whole number lengths in some unit? That would be disturbing, since we have infinitely many Pythagorean triples, 3-4-5, 5-12-13, etc. that form right angle triangles. Fortunately, the proof cannot be applied to these other cases. The self-similarity in these other cases does not require the hypotenuse to be divided exactly in half. That the hypotenuse ends up with an odd number length is no longer troublesome. That is fortunate, since all Pythagorean triples, reduced to their simplest ratios, have an odd number for the hypotenuse.

To Ponder

In Cartesian geometry, we cover the Euclidean plane with an x-y coordinate system. Geometric structures arise as algebraic formulae. A straight line is "y=mx+b," for example. Has the Pythagorean goal of founding geometry on numbers been realized here?

The analyses above show that √2 is irrational. What about other numbers? How common is it for a whole number to have an irrational square root? Are there proofs for these other cases?*

The golden ratio φ is reputed to be the most pleasing proportion for a rectangle and, for this reason, appears often in classical art. Its value is roughly 1.618, but the exact value is irrational. It has a simple geometric definition: take a rectangle whose sides are in the golden ratio; remove a square; and the remaining rectangle is still a golden rectangle. This fact enables a "shrinking geometrical proof" of the irrationality of φ.

The algebraic expression of this geometrical fact is that (φ-1) = 1/φ. Solve for φ. (You will need the quadratic formula.)

*Hint: the algebraic proof generalizes if we replace 2 by any number N that has no whole number square root. The geometric shrinking proof works best for the case of a rectangle with the ratio of sides √N to 1, divided into N smaller rectangles of the same shape. All these proofs fail if N has a whole number square root. The first step of all the proofs is to show that, if √N = p/q, then p is a multiple of N. This step fails since, if the square root is a whole number, then we can write √N = p/1. Then p is not a multiple of N.