![\begin{displaymath}
E = 2.303\frac{RT}{ZF} \log\frac{\left[C\right]_o}{\left[C\right]_i}\end{displaymath}](img3.gif)
This problem can be resolved if there is a means to keep the potential of the cable localized and high. This is exactly the problem that action potentials solve. In a real nerve cell there are many species of ions, calcium, potassium, sodium, chloride, magnesium, to name a few of the most common. The basis for the resting membrane potential is the balance of these ions in the cell and outside of the cell. There are basically two forces at work in absence of ionically selective channels: (i) passive diffusion in which case high concentrations tend to move toward low concentrations and (ii) electric forces which attempt to balance the charges on either side of the membrane.
Hodgkin and Huxley won the Nobel prize for their elegant experimental and theoretical work on the nature of the voltage gated channels in the squid axon. This theory is the basis for all subsequent models of ionic channels in nerve and other membranes. Some of the details may differ, but the basic ideas are the same.
Channels facilitate the passive flow of ions across the membrane. When they are gated by other forces such as calcium or voltage, they can also provide great computational properties to the neuron. Non-gated channels are responsible for the membrane potential. Recall that the equilibrium potential of an ion is given by:
![\begin{displaymath}
E = 2.303\frac{RT}{ZF} \log\frac{\left[C\right]_o}{\left[C\right]_i}\end{displaymath}](img3.gif)
![\begin{displaymath}
V_m = \frac{RT}{F}\ln \frac{\sum P_j \left[C_j\right]_o}
{\sum P_j \left[C_j\right]_i}\end{displaymath}](img6.gif)
PK:PNa:PCl=1:.04:.45
during the peak of the action potentialPK:PNa:PCl=1:20:.45
This is really the correct way to discern the membrane potential, however, in modeling, we will make a much simpler equivalent circuit. We will treat each ion channel as a conductor and a battery. Note that the permeabilities act like conductances and the equilibrium potentials act as batteries. Consider Figure 1 which ignores the pumps for sodium and potassium. Then the equations for the membrane are:
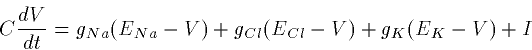 |
(1) |
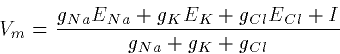
Homework:
![]() What is Vm?
What is Vm?
![]()
![]() is the effective conductance. Using the given values
for the potassium and sodium conductances and noting that
is the effective conductance. Using the given values
for the potassium and sodium conductances and noting that ![]() where A is the area of the membrane and using
where A is the area of the membrane and using ![]() what
is the area of the membrane if the time constant is 1msec. (Hint: The
time constant is
what
is the area of the membrane if the time constant is 1msec. (Hint: The
time constant is ![]() )
)