Voltage gated channels

The basis for the action potential is the voltage gated ion channel. That is the conductance of the channel is dependent on the membrane potential at the time. This throws a monkey wrench into the equilibrium potential since the conducatnces are actually nonlinear function of the voltage. As in Kandel and Schwartz, one can measure the properties of the action potential by voltage clamp studies in order to understand the basic dynamics of active channels. The idea is really just an application of Ohms law and we can thus write:  

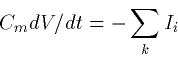$$C_m dV/dt = -\sum_k I_i$$ (2)

where I_i are just the different currents per unit area due to the channels. Each of these can be decomposed as:

There are at least 4 different types of channels:

1.

Passive

$$I_i=\bar{g}(V-\bar{E})$$

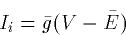
2.

Persistent or noninactivating

$$I_i = \bar{g}m(t)^p(V-\bar{E})$$

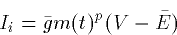
3.

Transient or inactivating

$$I_i = \bar{g}m(t)^ph(t)^q(V-\bar{E})$$

4.

Anomalous or activated by hyperpolarization

$$I_i = \bar{g}h(t)^q(V-\bar{E})$$

where m,h are dynamic variables that are in [0,1] and are generally voltage dependent. m will generally increase as the voltage increases and h decreases as the voltage increases. The powers, p,q are meant to represent the components of a channel. For example, the potassium channel consistes of 4 subunits and so the power is 4. The diagram in Figure 2 should make this clear.

 

Figure 2: The four different types of gated channels. (1) The passive gate lets ions through a a rate proportional to the voltage drop, (2) The persistent gate requires the ``m'' activating gate to be open, (3) the transient gate requires both the activating gate and the inactivating gate to be open, (4) the anomalous requires the inactivating gate to be open. The functions $m_\infty$ and $h_\infty$are shown in the figure

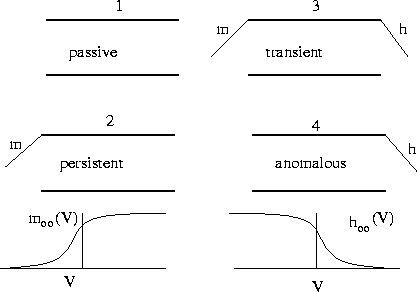In the squid axon, potassium is of type 2 (persistent noninactivating) and sodium is of type 3 (transient or inactivating.) In the thalamus, there is a type 3 calcium current that is very important for synchronizing spindle activity. Now lets examine the dynamics of the channel variables, m,h. The ideas are grounded in chemical kinetics and can be neatly summarized by the mass action model:

$$\begin{array} {c} \hbox{Closed} \ 1-m \end{array} \quad \... ...nd{array}\quad \begin{array} {c} \hbox{Open} \ m\end{array}$$

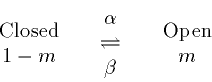
Using the law of mass action we get

$$\frac{dm}{dt} = \alpha(V)(1-m)-\beta(V)m$$

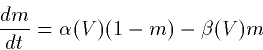
which we can rearrage to the better known form:  

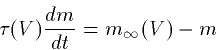$$\tau(V) \frac{dm}{dt} = m_\infty(V)-m$$ (3)

where

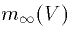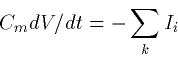
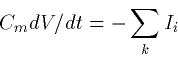
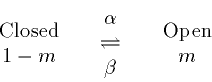
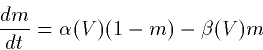
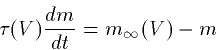
The key points to note in general are that (i) $m_\infty(V)$ is an increasing function of voltage for activating gates. That is, the higher the potential, the higer the probability of the activation gate being open. Figure 2 shows the typical activation function. (ii) Inactivation gates decrease with increased voltage and are generally slower than the activation gates. (iii) While the gates are generally dependent on voltage, some potassium gates depend on the intracellular calcium concentration or on other modulatory substances.