next up previous
Next: Some common currents in Up: Voltage gated channels Previous: Voltage gated channels

An aside on experimental issues: Voltage clamp

The equations for the gating variables are all well and good in theory, but in practice, how does one compute them? This is done by a technique known as the voltage clamp. One holds the voltage as a fixed value and then changes it by some incremental amount. The current that passes is then measured. Lets take, for example, the squid axon model of Hodgkin and Huxley. Suppose that we chemically block the sodium channel. (There are many different pharmacological agents that can be used to block different channels. Sodium is blocked by tetrodotoxin, TTX, found in the puffer fish. Tetraethylammonium , TEA, blocks certain kinds of potassium channels.) The the current passed is due solely to the leak, the capacitance, and the leak. Since the capacitative current is just a short pulse and is zero otherwise, we can ignore that. The current is thus:

I(t) = gL (V-EL)+gK(t)(V-EK)

We know the voltage and the reversal potentials, so we can solve for the time-dependent conductance:

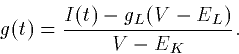
\begin{displaymath} g(t) = \frac{I(t)-g_L(V-E_L)}{V-E_K}.\end{displaymath}

Now, the idea is that the conductance should be of the form:

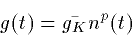
\begin{displaymath} g(t) = \bar{g_K} n^p(t)\end{displaymath}

where

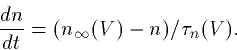
\begin{displaymath} \frac{dn}{dt} = (n_\infty(V) - n)/\tau_n(V).\end{displaymath}

For a fixed value of voltage, this is just a linear differential equation which has a solution:

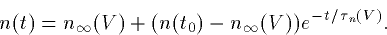
\begin{displaymath} n(t) = n_\infty(V)+ (n(t_0)-n_\infty(V)) e^{-t/\tau_n(V)}. \end{displaymath}

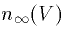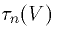By using a series of different initial voltages and voltage jumps, we can first find the best power, p to fit the data. Then we can find the maximal value of the conductance. Finally, we can use the above formula to fit the conductance to a series of exponential curves and use these to find $n_\infty(V)$ and $\tau_n(V)$ for each value of the voltage. For gates that have both activation and inactivation, the voltage clamp is a little trickier, but not all that bad. With the advent of channel blockers, it is now a fairly standard (though by no means easy!) experimental protocol. A paper illustrating the technique applied to a calcium current in the thalamus is Coulter et al J. Physiol. London, 414:587-604.

next up previous
Next: Some common currents in Up: Voltage gated channels Previous: Voltage gated channels
G. Bard Ermentrout
1/29/1998
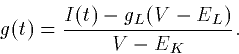
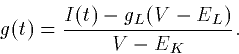
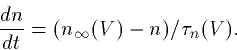