Some common currents in cortical and thalamic neurons

There are many different currents in the cortex and thalamus. I only touch on a few of them.

 

name ion type speed Rev. Pot threshold

I_Na Fast Sodium [Na] act/inact very fast 45 mV -50 mV

I_Nap Persistent Sodium [Na] act/inact(slow) fast 45 mV -65 mV

I_K Delayed rectifier [K] act fast -100 mV -40 mV

I_A A-current [K] act/inact fast -100 mV -60 mV

I_AHP Ca-dependent K [K] act (Ca-dep) moderate-slow -100 mV -

I_M Slow potassium [K] act slow -100 mV -35 mV

I_K2 Slow potassium [K] act/inact slow -100 mV -40 mV

I_T Transient Ca [Ca] act/inact slow 150 mV -60 mV

I_L High thresh. Ca [Ca] act fast 150 mV -10 mV

I_h Sag current [Ca]&[Na] inact slow 0-40 mV -

I_leak Leak [Cl],[K], [Na] passive - -60 mV -

Given the above table and the form for the kinetic parameters, $\alpha,\beta$ one can easily put together models for active membranes. This can be regarded as a kind of mix and match affair which results in a huge variety of models. In spite of this, there are virtually no differences between the fundamental models of cardiac, smooth muscle, squid axon, thalamic relay cells, etc. Each can be written as (2) where the I_k each satisfy  

$$I_k= \bar{g} m^ph^q(V-E)$$ (4)

and m,h satisfy equations like (3). In many cases, the calcium current is handled slightly different than the linear conductance model and instead, the constant field equation is used:

$$I_{Ca} = P m^ph^q \frac{(zFV)^2}{RT} \frac{[Ca_i]-[Ca_o]e^{-zFV/RT}}{1-e^{-zFV/RT}}$$

Here instead of conductance, the permeability is used.

The best known examples of these models are the Hodgkin-Huxley equations which have 3 currents, (i) passive leak, (ii) fast sodium, and (iii) delayed rectifier.

 

Figure 3: The three different functional forms for the gating rates. Only the increasing ones are shown; decreasing ones are just mirror images. All are chosen to pass through 0.5 at 0.

All of the currents mentioned in the table above have been found in cortical or thalamic neurons. These currents are responsible for the intrinsic firing properties of neurons which include three different types: (i) regular spiking neurons (ii) fast spike neurons (iii) bursting neurons.

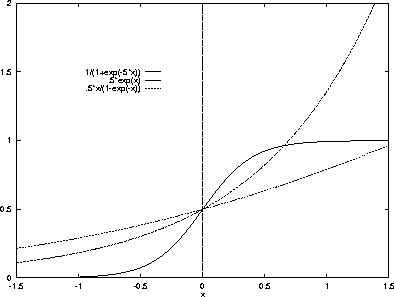
Recall that the typical channel gate satisfies

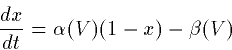
$$\frac{dx}{dt}= \alpha(V)(1-x)-\beta(V)$$

The functions $\alpha,\beta$ are generally of three different forms (see Figure 3)

1.

Exponential:

$$\alpha(v) = C_1 e^{(V-V_T)/V_s}$$

2.

Linear-Exponential:

$$\alpha(v) = C_1 (V-V_T)/(1-e^{(V-V_T)/V_s})$$

3.

Logistic:

$$\alpha(v) = C_1/(1+e^{-(V-V_T)/V_s})$$

All three are defined by 3 parameters, the magnitude, C₁, the ``threshold'', V_T and the slope at threshold, V_s.