Calcium dynamics and I_K-AHP

Most of the models that are commonly used treat the current as in (4) but we will see that calcium is somewhat special and requires a more complex approach.

Intracellular calcium is heavily buffered so that the concentration tends be be very low. As a consequence the reversal potential for calcium can not really be modeled as a fixed value. The intracellular calcium levels are on the order of 1000 times lower than extracellular calcium which accounts for the rather large reversal potential for calcium. The way that many researchers model calcium is through the constant field equation  

$$I_{Ca} = P_{Ca} m^ph^q \frac{4 F^2}{RT} V \left(\frac{[Ca]_{in} e^{2VF/RT} - [Ca]_{out}}{e^{2VF/RT}-1}\right)$$ (5)

where F=96480 Colombs/mole, 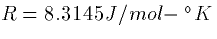$R=8.3145 J/mol-{}^\circ K$, P_Ca is the permeability, and T is the temperature in degrees Kelvin (centigrade plus 273).

NOTES:

• 1 V = 1 joule/ Coulomb
• Permeability is measured in cm/sec and concentration is in moles/liter or moles/cubic centimeter. Thus, the dimensions above are coulombs/(sec-square centimeter) which is just current per unit area.

To get some intuition behind this expression, define

$$E_{Ca} = \frac{RT}{2F}\ln\frac{[Ca]_{out}}{[Ca]_{in}}$$

as is usual. Then in the above, it is clear that V=E_Ca makes the current vanish so that the ``reversal potential'' is indeed the Nernst equilibrium for calcium and linearizing about this reversal potential, we get the slope

$$\bar{g}_{Ca} = \frac{2P_{Ca}F^3 E_{Ca}[Ca]_{out}/(RT)^2}{[Ca]_{out}/[Ca]_{in}-1}$$

which if you check has dimensions of conductance per unit area. Thus, we can approximate (5) by

$$I_{Ca} = \bar{g}_{Ca} (V - E_{Ca})$$

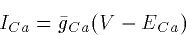
where E_Ca is the Nernst equilibrium potential. We will use the two interchangeably, but keep in mind that the constant field equation is more correct.